Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hughes, D. W.
and
Proctor, M. R. E.
2013.
The effect of velocity shear on dynamo action due to rotating convection.
Journal of Fluid Mechanics,
Vol. 717,
Issue. ,
p.
395.
Sridhar, S.
and
Singh, Nishant K.
2014.
Large-scale dynamo action due to α fluctuations in a linear shear flow.
Monthly Notices of the Royal Astronomical Society,
Vol. 445,
Issue. 4,
p.
3770.
Singh, Nishant K.
2016.
Moffatt-drift-driven large-scale dynamo due to fluctuations with non-zero correlation times.
Journal of Fluid Mechanics,
Vol. 798,
Issue. ,
p.
696.
Herreman, W.
2016.
Minimal flow perturbations that trigger kinematic dynamo in shear flows.
Journal of Fluid Mechanics,
Vol. 795,
Issue. ,
Singh, Nishant K.
Rogachevskii, Igor
and
Brandenburg, Axel
2017.
Enhancement of Small-scale Turbulent Dynamo by Large-scale Shear.
The Astrophysical Journal Letters,
Vol. 850,
Issue. 1,
p.
L8.
Teed, Robert J.
and
Proctor, Michael R. E.
2017.
Quasi-cyclic behaviour in non-linear simulations of the shear dynamo.
Monthly Notices of the Royal Astronomical Society,
Vol. 467,
Issue. 4,
p.
4858.
Jingade, Naveen
Singh, Nishant K.
and
Sridhar, S.
2018.
Generation of large-scale magnetic fields due to fluctuating in shearing systems.
Journal of Plasma Physics,
Vol. 84,
Issue. 6,
Biswas, Shishir
and
Ganesh, Rajaraman
2023.
Effect of flow shear on the onset of dynamos.
Physics of Plasmas,
Vol. 30,
Issue. 11,
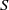 , growth rates increase no faster than
, growth rates increase no faster than 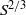 under plausible conditions on the amplitude of the remaining velocity.
under plausible conditions on the amplitude of the remaining velocity.