Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Maxeiner, Eric
Shakeri, Mostafa
and
Duncan, James H.
2011.
A parametric study of breaking bow waves using a 2D + T Technique.
Journal of Fluid Mechanics,
Vol. 687,
Issue. ,
p.
540.
Noblesse, Francis
Huang, Fuxin
and
Yang, Chi
2013.
The Neumann–Michell theory of ship waves.
Journal of Engineering Mathematics,
Vol. 79,
Issue. 1,
p.
51.
Noblesse, Francis
Delhommeau, Gerard
Liu, Hua
Wan, De-cheng
and
Yang, Chi
2013.
Ship bow waves.
Journal of Hydrodynamics,
Vol. 25,
Issue. 4,
p.
491.
Yang, Chi
Huang, Fuxin
and
Noblesse, Francis
2013.
Practical evaluation of the drag of a ship for design and optimization.
Journal of Hydrodynamics,
Vol. 25,
Issue. 5,
p.
645.
Noblesse, Francis
Huang, Fuxin
and
Yang, Chi
2013.
Evaluation of ship waves at the free surface and removal of short waves.
European Journal of Mechanics - B/Fluids,
Vol. 38,
Issue. ,
p.
22.
Huang, Fuxin
Yang, Chi
and
Noblesse, Francis
2013.
Numerical implementation and validation of the Neumann–Michell theory of ship waves.
European Journal of Mechanics - B/Fluids,
Vol. 42,
Issue. ,
p.
47.
Noblesse, Francis
Delhommeau, Gerard
Queutey, Patrick
and
Yang, Chi
2014.
An elementary analytical theory of overturning ship bow waves.
European Journal of Mechanics - B/Fluids,
Vol. 48,
Issue. ,
p.
193.
Delacroix, Sylvain
Germain, Grégory
Gaurier, Benoît
and
Billard, Jean-Yves
2016.
Experimental study of bubble sweep-down in wave and current circulating tank: Part I—Experimental set-up and observed phenomena.
Ocean Engineering,
Vol. 120,
Issue. ,
p.
78.
Delacroix, Sylvain
Germain, Grégory
Gaurier, Benoît
and
Billard, Jean-Yves
2016.
Experimental study of bubble sweep-down in wave and current circulating tank: Part II—Bubble clouds characterization.
Ocean Engineering,
Vol. 120,
Issue. ,
p.
88.
Riviere, N.
Vouaillat, G.
Launay, G.
and
Mignot, E.
2017.
Emerging Obstacles in Supercritical Open-Channel Flows: Detached Hydraulic Jump versus Wall-Jet-Like Bow Wave.
Journal of Hydraulic Engineering,
Vol. 143,
Issue. 7,
Ma, Chao
Zhu, Yi
He, Jiayi
Zhang, Chenliang
Wan, Decheng
Yang, Chi
and
Noblesse, Francis
2018.
Nonlinear corrections of linear potential-flow theory of ship waves.
European Journal of Mechanics - B/Fluids,
Vol. 67,
Issue. ,
p.
1.
Mallat, Bachar
Germain, Grégory
Billard, Jean-Yves
and
Gaurier, Benoit
2018.
A 3D study of the bubble sweep-down phenomenon around a 1/30 scale ship model.
European Journal of Mechanics - B/Fluids,
Vol. 72,
Issue. ,
p.
471.
He, Jiayi
Zhu, Yi
Ma, Chao
Yang, Chen-Jun
Li, Wei
and
Noblesse, Francis
2018.
Boundary integral representations of steady flow around a ship.
European Journal of Mechanics - B/Fluids,
Vol. 72,
Issue. ,
p.
152.
He, Jiayi
Wu, Huiyu
Yang, Chen-Jun
Zhu, Ren-Chuan
Li, Wei
and
Noblesse, Francis
2021.
Boundary-integral representation sans waterline integral for flows around ships steadily advancing in calm water.
European Journal of Mechanics - B/Fluids,
Vol. 89,
Issue. ,
p.
259.
Hu, Yiding
Liu, Cheng
Hu, Changhong
and
Wan, Decheng
2021.
Numerical investigation of flow structure and air entrainment of breaking bow wave generated by a rectangular plate.
Physics of Fluids,
Vol. 33,
Issue. 12,
Di Mascio, A.
Marrone, S.
Colagrossi, A.
Chiron, L.
and
Le Touzé, D.
2021.
SPH–FV coupling algorithm for solving multi-scale three-dimensional free-surface flows.
Applied Ocean Research,
Vol. 115,
Issue. ,
p.
102846.
He, Jiayi
Wu, Huiyu
Yang, Chen-Jun
Zhu, Ren-Chuan
Li, Wei
and
Noblesse, Francis
2021.
Diffraction–radiation of regular water waves and irregular frequencies: A straightforward flow-modeling approach and analysis.
European Journal of Mechanics - B/Fluids,
Vol. 90,
Issue. ,
p.
7.
Mallat, Bachar
Germain, Grégory
Billard, Jean-Yves
and
Gabillet, Céline
2022.
Breaking wave bubble measurements around ship model by optical probe.
Ocean Engineering,
Vol. 246,
Issue. ,
p.
110438.
Wang, Xiaocong
Zhu, Renchuan
and
Jiang, Yin
2023.
Numerical investigation on nonlinear ship waves by LCM and WSAM.
Ocean Engineering,
Vol. 284,
Issue. ,
p.
115076.
Hu, Yiding
Liu, Cheng
Zhao, Min
and
Hu, Changhong
2023.
High-fidelity simulation of an aerated cavity around a surface-piercing rectangular plate.
Physical Review Fluids,
Vol. 8,
Issue. 4,
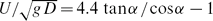 with g ≡ acceleration of gravity. These measurements of bow wave unsteadiness provide preliminary experimental validation of the foregoing simple theoretical relation for the boundary between the unsteady and overturning bow wave regimes for non-bulbous wedge-shaped ship bows with insignificant rake and flare. Extension of this relation to more complicated ship bows, notably bows with rake and flare, is also considered.
with g ≡ acceleration of gravity. These measurements of bow wave unsteadiness provide preliminary experimental validation of the foregoing simple theoretical relation for the boundary between the unsteady and overturning bow wave regimes for non-bulbous wedge-shaped ship bows with insignificant rake and flare. Extension of this relation to more complicated ship bows, notably bows with rake and flare, is also considered.