Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-25T04:25:46.036Z Has data issue: false hasContentIssue false
  • English
  • Français

A bound on the vertical transport of heat in the ‘ultimate’ state of slippery convection at large Prandtl numbers

Published online by Cambridge University Press:  18 July 2013

Xiaoming Wang  and
Jared P. Whitehead
Xiaoming Wang
Affiliation:
Department of Mathematics, Florida State University, Tallahassee, FL 32306, USA
Jared P. Whitehead*
Affiliation:
Center for Nonlinear Studies, Los Alamos National Laboratory, Los Alamos, NM 87545, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

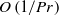An upper bound on the rate of vertical heat transport is established in three dimensions for stress-free velocity boundary conditions on horizontally periodic plates. A variation of the background method is implemented that allows negative values of the quadratic form to yield ‘small’ ($O\left(1/ \mathit{Pr}\right)$) corrections to the subsequent bound. For large (but finite) Prandtl numbers this bound is an improvement over the ‘ultimate’ 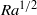$R{a}^{1/ 2} $ scaling and, in the limit of infinite 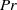$Pr$, agrees with the bound of 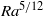$R{a}^{5/ 12} $ recently derived in that limit for stress-free boundaries.

JFM classification

Geophysical and Geological Flows: Mantle convection Turbulent Flows: Turbulent convection
Type
Papers
Information
Journal of Fluid Mechanics , Volume 729 , 25 August 2013 , pp. 103 - 122
Creative Commons
This is a work of the U.S. Government and is not subject to copyright protection in the United States.
Copyright
©2013 Cambridge University Press.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adams, R. & Fournier, J. 2003 Sobolev Spaces, 2nd edn. pp. 1–7. Elsevier.Google Scholar
Ahlers, G. 2009 Turbulent convection. Physics 2 (74), 7.CrossRefGoogle Scholar
Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large-scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.CrossRefGoogle Scholar
Ahlers, G., He, X., Funfschilling, D. & Bodenschatz, E. 2012 Heat transport by turbulent Rayleigh–Bénard convection for $Pr\simeq 0. 8$ and $3\times 1{0}^{12} \lesssim Ra\lesssim 1{0}^{15} $ : aspect ratio $\gamma = 0. 50$ . New J. Phys. 14, 103012.CrossRefGoogle Scholar
Amati, G., Koal, K., Massaioli, F., Sreenivasan, K. R. & Verzicco, R. 2005 Turbulent thermal convection at high Rayleigh numbers for a Boussinesq fluid of constant Prandtl number. Phys. Fluids 17, 121701.CrossRefGoogle Scholar
Bodenschatz, E., Pesch, W. & Ahlers, G. 2000 Recent developments in Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 32, 709–778.CrossRefGoogle Scholar
Busse, F. H. 1969 On Howard’s upper bound for heat transport by turbulent convection. J. Fluid Mech. 37, 457–477.CrossRefGoogle Scholar
Busse, F. H. 1989 Mantle Convection: Plate Tectonics and Global Dynamics, Chap. 2: Fundamentals of Thermal Convection. Gordon and Breach.Google Scholar
Busse, F. H., Swinney, H. & Gollub, J. 1985 Transition to turbulence in Rayleigh–Bénard convection. In Hydrodynamic Inotabilities and the Transition to Turbulence: Topics in Applied Physics, vol. 45, pp. 97–137. Springer.Google Scholar
Chini, G. P. & Cox, S. M. 2009 Large Rayleigh number thermal convection: heat flux predictions and strongly nonlinear solutions. Phys. Fluids 21, 083603.CrossRefGoogle Scholar
Constantin, P. & Doering, C. R. 1996 Heat transfer in convective turbulence. Nonlinearity 9, 1049–1060.CrossRefGoogle Scholar
Constantin, P. & Doering, C. R. 1999 Infinite Prandtl number convection. J. Stat. Phys. 94, 159–172.CrossRefGoogle Scholar
Constantin, P. & Foias, C. 1988 Navier–Stokes Equations. Chicago University Press.CrossRefGoogle Scholar
Corson, L. T. 2011 Maximizing the heat flux in steady unicellular porous media convection. Tech. Rep. Woods Hole Oceanographic Institution, WHOI Geophysical Fluid Dynamics Program Fellow Report.Google Scholar
Doering, C. R. & Constantin, P. 1996 Variational bounds on energy dissipation in incompressible flows. Part 3. Convection. Phys. Rev. E 53 (6), 5957–5981.CrossRefGoogle Scholar
Doering, C. R., Otto, F. & Reznikoff, M. G. 2006 Bounds on vertical heat transport for infinite-Prandtl-number Rayleigh–Bénard convection. J. Fluid Mech. 560, 229–241.CrossRefGoogle Scholar
Funfschilling, D., Bodenschatz, E. & Ahlers, G. 2009 Search for the ‘ultimate state’ in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 103, 014503.CrossRefGoogle Scholar
Getling, A. V. 1998 Rayleigh–Bénard Convection: Structures and Dynamics, 11. Advanced Series in Nonlinear Dynamics, World Scientific.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2001 Thermal convection for large Prandtl number. Phys. Rev. Lett. 86, 3316–3319.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2004 Fluctuations in turbulent Rayleigh–Bénard convection: the role of plumes. Phys. Fluids 16 (12), 4462–4472.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2011 Multiple scaling in the ultimate regime of thermal convection. Phys. Fluids 23, 045108.CrossRefGoogle Scholar
He, X., Funfschilling, D., Nobach, H., Bodenschatz, E. & Ahlers, G. 2012 Transition to the ultimate state of turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 108 (2), 024502.CrossRefGoogle Scholar
Howard, L. N. 1963 Heat transport by turbulent convection. J. Fluid Mech. 17, 405–432.CrossRefGoogle Scholar
Ierley, G. R., Kerswell, R. R. & Plasting, S. C. 2006 Infinite-Prandtl-number convection. Part 2. A singular limit of upper bound theory. J. Fluid Mech. 560, 159–227.CrossRefGoogle Scholar
Johnston, H. & Doering, C. R. 2009 Comparison of turbulent thermal convection between conditions of constant temperature and constant flux. Phys. Rev. Lett. 102, 064501.CrossRefGoogle ScholarPubMed
Kraichnan, R. H. 1962 Turbulent thermal convection at arbitrary Prandtl number. Phys. Fluids 5, 1374–1389.CrossRefGoogle Scholar
Malkus, W. V. R. 1954 The heat transport and spectrum of thermal turbulence. Proc. R. Soc. Lond. A 225, 196–212.Google Scholar
Otero, J. 2002 Bounds for the heat transport in turbulent convection. PhD thesis, Department of Mathematics, University of Michigan.Google Scholar
Otero, J., Wittenberg, R. W., Worthing, R. A. & Doering, C. R. 2002 Bounds on Rayleigh–Bénard convection with an imposed heat flux. J. Fluid Mech. 473, 191–199.CrossRefGoogle Scholar
Otto, F. & Seis, C. 2011 Rayleigh–Bénard convection: improved bounds on the Nusselt number. J. Math. Phys. 52, 083702.CrossRefGoogle Scholar
Plasting, S. C. & Ierley, G. R. 2005 Estimates of heat transport in infinite Prandtl number convection. Part 1. Conservative bounds. J. Fluid Mech. 542, 343–363.CrossRefGoogle Scholar
Plasting, S. C. & Kerswell, R. R. 2003 Improved upper bound on the energy dissipation rate in plane Couette flow: the full solutions to Busse’s problem and the Constantin–Doering–Hopf problem with one-dimensional background fields. J. Fluid Mech. 477, 363–379.CrossRefGoogle Scholar
Rayleigh, Lord 1916 On convection currents in a horizontal layer of fluid, when the higher temperature is on the under side. Phil. Mag. J. Sci. 32 (192), 529–546.CrossRefGoogle Scholar
Shishkina, O., Stevens, R. J. A. M., Grossmann, S. & Lohse, D. 2010 Boundary layer structure in turbulent thermal convection and its consequences for the required numerical resolution. New J. Phys. 12, 075022.CrossRefGoogle Scholar
Sparrow, E. M., Goldstein, R. J. & Jonsson, V. K. 1963 Thermal instability in a horizontal fluid layer: effect of boundary conditions and nonlinear temperature profiles. J. Fluid Mech. 18, 513–528.CrossRefGoogle Scholar
Stevens, R. J. A. M., Lohse, D. & Verzicco, R. 2011 Prandtl and Rayleigh number dependence of heat transport in high Rayleigh number thermal convection. J. Fluid Mech. 688, 31–43.CrossRefGoogle Scholar
Stevens, R. J. A. M., van der Poel, E. P., Grossmann, S. & Lohse, D. 2013 The unifying theory of scaling in thermal convection: the updated prefactors. J. Fluid Mech. (submitted).CrossRefGoogle Scholar
Stevens, R. J. A. M., Verzicco, R. & Lohse, D. 2010 Radial boundary layer structure and Nusselt number in Rayleigh–Bénard convection. J. Fluid Mech. 643, 495–507.CrossRefGoogle Scholar
Temam, R. 2000 Navier–Stokes Equations. AMS.Google Scholar
Urban, P., Hanzelka, P., Kralik, T., Musilova, V., Srnka, A. & Skrbek, L. 2012 Effect of boundary layers asymmetry on heat transfer efficiency in turbulent Rayleigh–Bénard convection at very high Rayleigh numbers. Phys. Rev. Lett. 109, 154301.CrossRefGoogle ScholarPubMed
Urban, P., Musilová, V. & Skrbek, L. 2011 Efficiency of heat transfer in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 107, 014302.CrossRefGoogle ScholarPubMed
Wang, X. 2005 A note on long time behavior of solutions to the Boussinesq system at large Prandtl number. Contemp. Maths 371, 315–323.CrossRefGoogle Scholar
Wang, X. 2007 Asymptotic behavior of global attractors to the Boussinesq system for Rayleigh–Bénard convection at large Prandtl number. Commun. Pure Appl. Maths 60 (9), 1293–1318.CrossRefGoogle Scholar
Wang, X. 2008a Bound on vertical heat transport at large Prandtl number. Physica D 237, 854–858.CrossRefGoogle Scholar
Wang, X. 2008b Stationary statistical properties of Rayleigh–Bénard convection at large Prandtl number. Commun. Pure Appl. Maths 61, 789–815.CrossRefGoogle Scholar
Whitehead, J. P. & Doering, C. R. 2011 The ultimate regime of two-dimensional Rayleigh–Bénard convection with stress-free boundaries. Phys. Rev. Lett. 106, 244501.CrossRefGoogle Scholar
Whitehead, J. P. & Doering, C. R. 2012 Rigid rigorous bounds on heat transport in a slippery container. J. Fluid Mech. 707, 241–259.CrossRefGoogle Scholar
Whitehead, J. P. & Wittenberg, R. 2013 Persistent logarithms: bounds on the transport of heat at infinite Prandtl number for no-slip, mixed thermal boundaries (in preparation).Google Scholar
Wittenberg, R. W. 2010 Bounds on Rayleigh–Bénard convection with imperfectly conducting plates. J. Fluid Mech. 665, 158–198.CrossRefGoogle Scholar