Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-28T21:15:30.706Z Has data issue: false hasContentIssue false
  • English
  • Français

Biglobal instabilities of compressible open-cavity flows

Published online by Cambridge University Press:  03 August 2017

Yiyang Sun Open the ORCID record for Yiyang Sun [Opens in a new window] ,
Kunihiko Taira Open the ORCID record for Kunihiko Taira [Opens in a new window] ,
Louis N. Cattafesta III  and
Lawrence S. Ukeiley
Yiyang Sun*
Affiliation:
Department of Mechanical Engineering, Florida State University, Tallahassee, FL 32310, USA
Kunihiko Taira
Affiliation:
Department of Mechanical Engineering, Florida State University, Tallahassee, FL 32310, USA
Louis N. Cattafesta III
Affiliation:
Department of Mechanical Engineering, Florida State University, Tallahassee, FL 32310, USA
Lawrence S. Ukeiley
Affiliation:
Department of Mechanical and Aerospace Engineering, University of Florida, Gainesville, FL 32611, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The stability characteristics of compressible spanwise-periodic open-cavity flows are investigated with direct numerical simulation (DNS) and biglobal stability analysis for rectangular cavities with aspect ratios of 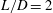$L/D=2$ and 6. This study examines the behaviour of instabilities with respect to stable and unstable steady states in the laminar regime for subsonic as well as transonic conditions where compressibility plays an important role. It is observed that an increase in Mach number destabilizes the flow in the subsonic regime and stabilizes the flow in the transonic regime. Biglobal stability analysis for spanwise-periodic flows over rectangular cavities with large aspect ratio is closely examined in this study due to its importance in aerodynamic applications. Moreover, biglobal stability analysis is conducted to extract two-dimensional (2-D) and 3-D eigenmodes for prescribed spanwise wavelengths $\unicode[STIX]{x1D706}/D$ about the 2-D steady state. The properties of 2-D eigenmodes agree well with those observed in the 2-D nonlinear simulations. In the analysis of 3-D eigenmodes, it is found that an increase of Mach number stabilizes dominant 3-D eigenmodes. For a short cavity with $L/D=2$, the 3-D eigenmodes primarily stem from centrifugal instabilities. For a long cavity with 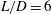$L/D=6$, other types of eigenmodes appear whose structures extend from the aft-region to the mid-region of the cavity, in addition to the centrifugal instability mode located in the rear part of the cavity. A selected number of 3-D DNS are performed at $M_{\infty }=0.6$ for cavities with 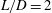$L/D=2$ and 6. For 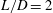$L/D=2$, the properties of 3-D structures present in the 3-D nonlinear flow correspond closely to those obtained from linear stability analysis. However, for 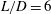$L/D=6$, the 3-D eigenmodes cannot be clearly observed in the 3-D DNS due to the strong nonlinearity that develops over the length of the cavity. In addition, it is noted that three-dimensionality in the flow helps alleviate violent oscillations for the long cavity. The analysis performed in this paper can provide valuable insights for designing effective flow control strategies to suppress undesirable aerodynamic and pressure fluctuations in compressible open-cavity flows.

JFM classification

Compressible Flows: Compressible Flows Instability: Instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 826 , 10 September 2017 , pp. 270 - 301
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahuja, K. K. & Mendoza, J.1995 Effects of cavity dimensions, boundary layer and temperature on cavity noise with emphasis on benchmark data to validate computational aeroacoustic codes. Final Report Contract NAS1-19061, Task 13. NASA Contractor Report.Google Scholar
Åkervik, E., Brandt, L., Henningson, D. S., Hœpffner, J., Marxen, O. & Schlatter, P. 2006 Steady solutions of the Navier–Stokes equations by selective frequency damping. Phys. Fluids 18, 068-102.Google Scholar
Arunajatesan, S., Barone, M. F., Wagner, J. L., Casper, K. M. & Beresh, S. J.2014 Joint experimental/computational inversigation into the effects of finite width on transonic cavity flow. AIAA Paper 2014-3027.Google Scholar
Beresh, S. J., Wagner, J. L. & Casper, K. M. 2016 Compressibility effects in the shear layer over a rectangular cavity. J. Fluid Mech. 808, 116–152.CrossRefGoogle Scholar
Beresh, S. J., Wagner, J. L., Pruett, B. O. M., Henfling, J. F. & Spillers, R. W. 2015 Supersonic flow over a finite-width rectangular cavity. AIAA J. 53 (2), 296–310.Google Scholar
Bergamo, L. F., Gennaro, E. M., Theofilis, V. & Medeiros, M. A. F. 2015 Compressible modes in a square lid-driven cavity. Aerosp. Sci. Technol. 44 (C), 125–134.Google Scholar
Brès, G. A.2007 Numerical simulations of three-dimensional instabilities in cavity flows. PhD thesis, California Institute of Technology.Google Scholar
Brès, G. A. & Colonius, T. 2008 Three-dimensional instabilities in compressible flow over open cavities. J. Fluid Mech. 599, 309–339.Google Scholar
Brès, G. A., Ham, F. E., Nichols, J. W. & Lele, S. K. 2017 Unstructured large-eddy simulations of supersonic jets. AIAA J. 55 (4), 1164–1184.Google Scholar
Cattafesta, L. N., Garg, S., Choudhari, M. & Li, F.1997 Active control of flow-induced cavity resonance. AIAA Paper 1997-1804.Google Scholar
Cattafesta, L. N. & Sheplak, M. 2011 Actuators for active flow control. Annu. Rev. Fluid Mech. 43, 247–272.CrossRefGoogle Scholar
Cattafesta, L. N., Song, Q., Williams, D. R., Rowley, C. W. & Alvi, F. S. 2008 Active control of flow-induced cavity oscillations. Prog. Aeronaut. Sci. 44, 479–502.Google Scholar
Colonius, T., Basu, A. J. & Rowley, C. W.1999 Numerical investigation of the flow past a cavity. AIAA Paper 1999–1912.CrossRefGoogle Scholar
Freund, J. B. 1997 Proposed inflow/outflow boundary condition for direct computation of aerodynamic sound. AIAA J. 35 (4), 740–742.Google Scholar
George, B., Ukeiley, L., Cattafesta, L. N. & Taira, K.2015 Control of three-dimensional cavity flow using leading edge slot blowing. AIAA Paper 2015-1059.CrossRefGoogle Scholar
Gharib, M. & Roshko, A. 1987 The effect of flow oscillations on cavity drag. J. Fluid Mech. 177, 501–530.Google Scholar
Heller, H. H. & Bliss, D. B.1975 The physical mechanism of flow-induced pressure fluctuations in cavities and concepts for their suppression. AIAA Paper 1975-491.Google Scholar
Kegerise, M. A., Spina, E. F., Garg, S. & Catttafesta, L. N. 2004 Mode-switching and nonlinear effects in compressible flow over a cavity. Phys. Fluids 16 (3), 678–686.Google Scholar
Khalighi, Y., Ham, F., Moin, P., Lele, S., Schlinker, R., Reba, R. & Simonich, J.2011a Noise prediction of pressure-mismatched jets using unstructured large eddy simulation. Proceedings of ASME Turbo Expo, Vancouver.Google Scholar
Khalighi, Y., Nichols, J. W., Ham, F., Lele, S. K. & Moin, P.2011b Unstructured large eddy simulation for prediction of noise issued from turbulent jets in various configurations. AIAA Paper 2011–2886.Google Scholar
Krishnamurty, K.1956 Sound radiation from surface cutouts in high speed flow. PhD thesis, California Institute of Technology.Google Scholar
Lawson, S. J. & Barakos, G. N. 2011 Review of numerical simulations for high-speed, turbulent cavity flows. Prog. Aeronaut. Sci. 47, 186–216.Google Scholar
Liu, Q., Gómez, F. & Theofilis, V. 2016 Linear instability analysis of low-Re incompressible flow over a long rectangular finite-span open cavity. J. Fluid Mech. 799, R2.CrossRefGoogle Scholar
Lusk, T., Cattafesta, L. & Ukeiley, L. S. 2012 Leading-edge slot blowing on an open cavity in supersonic flow. Exp. Fluids 53, 187–199.Google Scholar
Maull, D. J. & East, L. F. 1963 Three-dimensional flow in cavities. J. Fluid Mech. 16, 620–632.Google Scholar
Meseguer-Garrido, F., de Vicente, J., Valero, E. & Theofilis, V. 2014 On linear instability mechanisms in incompressible open cavity flow. J. Fluid Mech. 752, 219–236.Google Scholar
Rockwell, D. & Naudascher, E. 1978 Review-self-sustaining oscillations of flow past cavities. Trans. ASME J. Fluids Engng 100, 152–165.Google Scholar
Rossiter, J. E.1964 Wind-tunnel experiments on the flow over rectangular cavities at subsonic and transonic speeds. Tech. Rep. 3438. Aeronautical Research Council Reports and Memoranda.Google Scholar
Rowley, C. W., Colonius, T. & Basu, A. J. 2002 On self-sustained oscillations in two-dimensional compressible flow over rectangular cavities. J. Fluid Mech. 455, 315–346.Google Scholar
Samimy, M., Kim, J. H., Kastner, J., Adamovich, I. & Utkin, Y. 2007 Active control of high-speed and high-Reynolds-number jets using plasma actuators. J. Fluid Mech. 578, 305–330.Google Scholar
Sarohia, V.1975 Experimental and analytical investigation of oscillations in flows over cavities. PhD thesis, California Institute of Technology.CrossRefGoogle Scholar
Sorensen, D., Lehoucq, R., Yang, C. & Maschhoff, K.1996–2008 ARPACK software.Google Scholar
Sun, Y., Nair, A. G., Taira, K., Cattafesta, L. N., Brès, G. A. & Ukeiley, L. S.2014 Numerical simulation of subsonic and transonic open-cavity flows. AIAA Paper 2014-3092.Google Scholar
Sun, Y., Taira, K., Cattafesta, L. N. & Ukeiley, L. S. 2016a Spanwise effects on instabilities of compressible flow over a long rectangular cavity. Theor. Comput. Fluid Dyn. (in press).Google Scholar
Sun, Y., Zhang, Y., Taira, K., Cattafesta, L., George, B. & Ukeiley, L.2016b Width and sidewall effects on high speed cavity flows. AIAA Paper 2016-1343.CrossRefGoogle Scholar
Theofilis, V. 2003 Advances in global linear instability analysis of nonparallel and three-dimensional flows. Prog. Aeronaut. Sci. 39, 249–315.Google Scholar
Theofilis, V. & Colonius, T.2004 Three-dimensional instabilities of compressible flow over open cavities: direct solution of the biglobal eigenvalue problem. AIAA Paper 2004-2544.Google Scholar
Toro, E. F. 2009 Riemann Solvers and Numerical Methods for Fluid Dynamics. Springer.CrossRefGoogle Scholar
de Vicente, J., Basley, J., Meseguer-Garrido, F., Soria, J. & Theofilis, V. 2014 Three-dimensional instabilities over a rectangular open cavity: from linear stability analysis to experimentation. J. Fluid Mech. 748, 189–220.Google Scholar
White, F. 1991 Viscous Fluid Flow. McGraw-Hill.Google Scholar
Yamouni, S., Sipp, D. & Jacquin, L. 2013 Interaction between feedback aeroacoustic and acoustic resonance mechanisms in a cavity flow: a global stability analysis. J. Fluid Mech. 717, 134–165.Google Scholar
Zdravkovich, M. M. 1981 Review and classification of various aerodynamic and hydrodynamic means for suppressing vortex shedding. J. Wind Engng Ind. Aerodyn. 7 (2), 145–189.Google Scholar
Zhang, K. & Naguib, A. M. 2011 Effect of finite cavity width on flow oscillation in a low-Mach-number cavity flow. Exp. Fluids 51 (5), 1209–1229.Google Scholar
Zhang, Y., Sun, Y., Arora, N., Cattafesta, L., Taira, K. & Ukeiley, L.2015 Suppression of cavity oscillations via three-dimensional steady blowing. AIAA Paper 2015-3219.Google Scholar