Published online by Cambridge University Press: 21 December 2018
This study deals with the transition toward quasi-periodicity of buoyant convection generated by a horizontal temperature gradient in a three-dimensional parallelepipedic cavity with dimensions 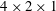 $4\times 2\times 1$ (length
$4\times 2\times 1$ (length  $\times$ width
$\times$ width  $\times$ height). Numerical continuation techniques, coupled with an Arnoldi method, are used to locate the steady and Hopf bifurcation points as well as the different steady and periodic flow branches emerging from them for Prandtl numbers ranging from 0 to 0.025 (liquid metals). Our results highlight the existence of two steady states along with many periodic cycles, all with different symmetries. The bifurcation scenarios consist of complex paths between these different solutions, giving a succession of stable flow states as the Grashof number is increased, from steady to periodic and quasi-periodic. The change of these scenarios with the Prandtl number, in connection with the crossing of bifurcation points, was carefully analysed.
$\times$ height). Numerical continuation techniques, coupled with an Arnoldi method, are used to locate the steady and Hopf bifurcation points as well as the different steady and periodic flow branches emerging from them for Prandtl numbers ranging from 0 to 0.025 (liquid metals). Our results highlight the existence of two steady states along with many periodic cycles, all with different symmetries. The bifurcation scenarios consist of complex paths between these different solutions, giving a succession of stable flow states as the Grashof number is increased, from steady to periodic and quasi-periodic. The change of these scenarios with the Prandtl number, in connection with the crossing of bifurcation points, was carefully analysed.