Article contents
The behaviour of Tollmien–Schlichting waves undergoing small-scale localised distortions
Published online by Cambridge University Press: 03 March 2016
Abstract
This paper is concerned with the behaviour of Tollmien–Schlichting (TS) waves experiencing small localised distortions within an incompressible boundary layer developing over a flat plate. In particular, the distortion is produced by an isolated roughness element located at 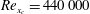 $\mathit{Re}_{x_{c}}=440\,000$. We considered the amplification of an incoming TS wave governed by the two-dimensional linearised Navier–Stokes equations, where the base flow is obtained from the two-dimensional nonlinear Navier–Stokes equations. We compare these solutions with asymptotic analyses which assume a linearised triple-deck theory for the base flow and determine the validity of this theory in terms of the height of the small-scale humps/indentations taken into account. The height of the humps/indentations is denoted by
$\mathit{Re}_{x_{c}}=440\,000$. We considered the amplification of an incoming TS wave governed by the two-dimensional linearised Navier–Stokes equations, where the base flow is obtained from the two-dimensional nonlinear Navier–Stokes equations. We compare these solutions with asymptotic analyses which assume a linearised triple-deck theory for the base flow and determine the validity of this theory in terms of the height of the small-scale humps/indentations taken into account. The height of the humps/indentations is denoted by 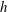 $h$, which is considered to be less than or equal to
$h$, which is considered to be less than or equal to 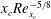 $x_{c}\mathit{Re}_{x_{c}}^{-5/8}$ (corresponding to
$x_{c}\mathit{Re}_{x_{c}}^{-5/8}$ (corresponding to 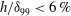 $h/{\it\delta}_{99}<6\,\%$ for our choice of
$h/{\it\delta}_{99}<6\,\%$ for our choice of 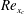 $\mathit{Re}_{x_{c}}$). The rescaled width
$\mathit{Re}_{x_{c}}$). The rescaled width 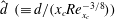 $\hat{d}~(\equiv d/(x_{c}\mathit{Re}_{x_{c}}^{-3/8}))$ of the distortion is of order
$\hat{d}~(\equiv d/(x_{c}\mathit{Re}_{x_{c}}^{-3/8}))$ of the distortion is of order 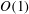 $\mathit{O}(1)$ and the width
$\mathit{O}(1)$ and the width 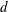 $d$ is shorter than the TS wavelength (
$d$ is shorter than the TS wavelength (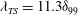 ${\it\lambda}_{TS}=11.3{\it\delta}_{99}$). We observe that, for distortions which are smaller than 0.1 of the inner deck height (
${\it\lambda}_{TS}=11.3{\it\delta}_{99}$). We observe that, for distortions which are smaller than 0.1 of the inner deck height (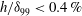 $h/{\it\delta}_{99}<0.4\,\%$), the numerical simulations confirm the asymptotic theory in the vicinity of the distortion. For larger distortions which are still within the inner deck (
$h/{\it\delta}_{99}<0.4\,\%$), the numerical simulations confirm the asymptotic theory in the vicinity of the distortion. For larger distortions which are still within the inner deck (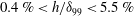 $0.4\,\%<h/{\it\delta}_{99}<5.5\,\%$) and where the flow is still attached, the numerical solutions show that both humps and indentations are destabilising and deviate from the linear theory even in the vicinity of the distortion. We numerically determine the transmission coefficient which provides the relative amplification of the TS wave over the distortion as compared to the flat plate. We observe that for small distortions,
$0.4\,\%<h/{\it\delta}_{99}<5.5\,\%$) and where the flow is still attached, the numerical solutions show that both humps and indentations are destabilising and deviate from the linear theory even in the vicinity of the distortion. We numerically determine the transmission coefficient which provides the relative amplification of the TS wave over the distortion as compared to the flat plate. We observe that for small distortions, 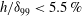 $h/{\it\delta}_{99}<5.5\,\%$, where the width of the distortion is of the order of the boundary layer, a maximum amplification of only 2 % is achieved. This amplification can however be increased as the width of the distortion is increased or if multiple distortions are present. Increasing the height of the distortion so that the flow separates (
$h/{\it\delta}_{99}<5.5\,\%$, where the width of the distortion is of the order of the boundary layer, a maximum amplification of only 2 % is achieved. This amplification can however be increased as the width of the distortion is increased or if multiple distortions are present. Increasing the height of the distortion so that the flow separates (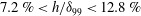 $7.2\,\%<h/{\it\delta}_{99}<12.8\,\%$) leads to a substantial increase in the transmission coefficient of the hump up to 350 %.
$7.2\,\%<h/{\it\delta}_{99}<12.8\,\%$) leads to a substantial increase in the transmission coefficient of the hump up to 350 %.
JFM classification
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 28
- Cited by



