Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-23T04:54:29.425Z Has data issue: false hasContentIssue false
  • English
  • Français

Behaviour of rarefied gas flow near the junction of a suddenly expanding tube

Published online by Cambridge University Press:  18 December 2013

Vijay Varade ,
Amit Agrawal  and
A. M. Pradeep
Vijay Varade
Affiliation:
Centre for Research in Nanotechnology and Science, Indian Institute of Technology Bombay, Mumbai, 400076, India
Amit Agrawal*
Affiliation:
Department of Mechanical Engineering, Indian Institute of Technology Bombay, Mumbai, 400076, India
A. M. Pradeep
Affiliation:
Department of Aerospace Engineering, Indian Institute of Technology Bombay, Mumbai, 400076, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

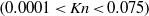This paper presents an experimental study of isothermal rarefied gas flow through a tube with sudden expansion in the slip flow regime. The measurements reported here are for nitrogen flowing at low pressures in conventional tubes with sudden expansion area ratios of 1.48, 3.74, 12.43 and 64. The flow is dynamically similar to gas flow in a microchannel as the Knudsen number $(0. 0001\lt \mathit{Kn}\lt 0. 075)$ falls in the slip flow regime; the Reynolds number in the smaller section (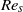${\mathit{Re}}_{s} $) ranges between 0.2 and 837. The static pressure along the wall is measured for different mass flow rates controlled by a mass flow controller and analysed to understand the flow behaviour. The velocity profiles are obtained through a momentum balance and using the pressure measurements. A discontinuity in the slope of pressure at the sudden expansion junction is noted and given special attention. The absence of flow separation is another key feature observed from the measurements. The streamlines are found to be concave near the junction. It is demonstrated that the flow ‘senses’ the oncoming sudden expansion junction and starts adjusting itself much before reaching the junction; this interesting behaviour is attributed to an increased axial momentum diffusion and wall slip. The additional acceleration of the central core of the gas flow causes an increase in the wall shear stress and a larger pressure drop as compared with a straight tube. These results are not previously available and should help in improving understanding of gaseous slip flows.

JFM classification

Micro-/Nano-fluid dynamics: Micro-/Nano-fluid dynamics Micro-/Nano-fluid dynamics: Non-continuum effects Rarefied Gas Flow: Rarefied Gas Flow
Type
Papers
Information
Journal of Fluid Mechanics , Volume 739 , 25 January 2014 , pp. 363 - 391
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdelall, F. F., Hahn, G, Ghiaasiaan, S. M., Abdel-Khalik, S. I., Jeter, S. S., Yoda, M. & Sadowski, D. L. 2005 Pressure drop caused by abrupt flow area changes in small channels. Exp. Therm. Fluid Sci. 29, 425–434.Google Scholar
Agrawal, A. 2011 A comprehensive review of gas flow in microchannels. Intl J. Micro-Nanoscale Transport 2 (1), 1–40.Google Scholar
Agrawal, A. & Agrawal, A. 2006 Three-dimensional simulation of gaseous slip flow in different aspect ratio microducts. Phys. Fluids 18, 103604.CrossRefGoogle Scholar
Agrawal, A., Djenidi, L. & Antonia, R. A. 2005 Simulation of gas flow in microchannels with a sudden expansion or contraction. J. Fluid Mech. 530, 135–144.Google Scholar
Agrawal, A. & Prabhu, S. V. 2008 Survey on measurement of tangential momentum accommodation coefficient. J. Vacuum Sci. Technol. A 26, 634–645.Google Scholar
Alexeenko, A. A., Gimelshein, S. F. & Levin, D. A. 2005 Reconsideration of low Reynolds number flow through constriction microchannels using the DSMC method. J. Microelctromech. Syst. 14, 847–856.CrossRefGoogle Scholar
Arkilic, E. B., Schimidt, M. A. & Breuer, K. S. 1997 Gaseous slip flow in long micro-channels. J. Microelectromech. Syst. 6, 167–178.Google Scholar
Barber, R. W. & Emerson, D. R. 2001 A numerical investigation of low Reynolds number gaseous slip flow at the entrance of circular and parallel plate microchannels. ECCOMAS Computational Fluid Dynamics Conference Swansea, Wales, UK, 4–7 September 2001. European Community on Computational Methods in Applied Sciences.Google Scholar
Celik, B. & Edis, F. O. 2007 Computational investigation of micro backward-facing step duct flow in slip regime. Nanoscale Microscale Thermophys. Engng 11, 319–331.CrossRefGoogle Scholar
Cercignani, C. 1964 Higher-order slip according to the linearized Boltzmann equation. rep. AS64-19, Institute of Engineering Research, Berkeley.Google Scholar
Cercignani, C. & Lorenzani, S. 2010 Variational derivation of second-order slip coefficients on the basis of the Boltzmann equation for hard-sphere molecules. Phys. Fluids 22, 062004.Google Scholar
Chalfi, T. Y. & Ghiaasiaan, S. M. 2008 Pressure drop caused by flow area changes in capillaries under low flow conditions. Intl J. Multiphase Flow 34, 2–12.Google Scholar
Chen, R. Y. 1973 Flow in the entrance region at low Reynolds numbers. Trans. ASME: J. Fluids Engng 95, 153–158.Google Scholar
Dagtekin, I. & Unsal, M. 2011 Numerical analysis of axisymmetric and planer sudden expansion flows for laminar regime. Intl J. Numer. Meth. Fluids 65, 1133–1144.CrossRefGoogle Scholar
Darbandi, M. & Roohi, E. 2011 DSMC simulation of subsonic flow through nanochannels and micro/nano backward-facing steps. Intl Commun. Heat Mass Transfer 38, 1443–1448.CrossRefGoogle Scholar
Demsis, A., Prabhu, S. V. & Agrawal, A. 2010 Influence of wall condition on friction factor for flow of gases under slip condition. Exp. Therm. Fluid Sci. 348, 1448–1455.CrossRefGoogle Scholar
Demsis, A., Verma, B, Prabhu, S. V. & Agrawal, A. 2009 Experimental determination of heat transfer coefficient in the slip regime and its anomalously low value. Phys. Rev. E 80, 016311.Google Scholar
Dombrowski, N., Foumeny, E. A., Ookawara, S. & Riza, A. 1993 The influence of Reynolds number on the entry length and pressure drop for laminar pipe flow. Can. J. Chem. Engng 71, 472–476.Google Scholar
Dongari, N., Agrawal, A. & Agrawal, A. 2007 Analytical solution of gaseous slip flow in long microchannels. Intl J. Heat Mass Transfer 50, 3411–3421.Google Scholar
Durst, F., Melling, A. & Whitelaw, J. H. 1974 Low Reynolds number flow over a plane symmetric sudden expansion. J. Fluid Mech. 641, 111–128.Google Scholar
Duryodhan, V. S., Singh, S. G. & Agrawal, A. 2013 Liquid flow through a diverging microchannel. Microfluid Nanofluid 14, 53–67.Google Scholar
Ewart, T., Perrier, P., Graur, I. A. & Meolans, J. G. 2006 Mass flow rate measurements in gas microflows. Exp. Fluids 41, 487–498.CrossRefGoogle Scholar
Ewart, T., Perrier, P., Graur, I. A. & Meolans, J. G. 2007 Mass flow rate measurements in a microchannel, from hydrodynamic to near free molecular regimes. J. Fluid Mech. 584, 337–356.Google Scholar
Friedmann, M, Gillis, J. & Liron, N. 1968 Laminar flow in a pipe at low and moderate Reynolds numbers. Appl. Sci. Res. 19, 426–438.Google Scholar
Goharzadeh, A. & Rodgers, P. 2009 Experimental measurement of laminar axisymmetric flow through confined annular geometries with sudden inward expansion. J. Fluids Engng 131, 124501.Google Scholar
Hammad, K. J., Otugen, M. V. & Arik, E. B. 1999 A PIV study of the laminar axisymmetric sudden expansion flow. Exp. Fluids 26, 266–272.Google Scholar
Harley, J., Huang, Y., Bau, H. & Zemel, J. N. 1995 Gas flow in microchannels. J. Fluid Mech. 284, 257–274.Google Scholar
Kursun, U. & Kapat, J. S. 2007 Modelling of microscale gas flows in transition regime part I: flow over backward facing steps. Nanoscale Microscale Thermophys. Engng 11, 15–30.Google Scholar
Lee, W. Y, Wong, M. & Zohar, Y. 2002 Microchannels in series connected via a contraction/expansion section. J. Fluid Mech. 459, 187–206.Google Scholar
Liou, T. M. & Lin, C. T. 2013 Study on microchannel flows with a sudden contraction–expansion at a wide range of Knudsen number using lattice Boltzmann method. Microfluid Nanofluid doi:10.1007/s10404-013-1200-2.CrossRefGoogle Scholar
Macagno, E. O. & Hung, T. K. 1967 Computational and experimental study of a captive annular eddy. J. Fluid Mech. 28 (1), 43–64.Google Scholar
Morini, G. L., Lorenzini, M. & Salvigni, S. 2006 Friction characteristics of compressible gas flows in microtubes. Exp. Therm. Fluid Sci. 30 (8), 733–744.Google Scholar
Oliveira, P. J. & Pinho, F. T. 1997 Pressure drop coefficient of laminar Newtonian flow in axisymmetric sudden expansions. Intl J. Heat Fluid Flow 18, 518–529.Google Scholar
Pan, C. T., Chuang, H. S., Cheng, C. Y. & Yang, C. T. 2004 Micro-flow measurement with a laser diode micro-particle image velocimetry. Sensors Actuators A 116, 51–58.Google Scholar
Pitakarnnop, J., Varoutis, S., Valougeorgis, D., Geoffroy, S., Baldas, L. & Colin, S. 2010 A novel experimental setup for gas microflows. Microfluid Nanofluid 8, 57–72.Google Scholar
Pong, K., Ho, C., Liu, J. & Tai, Y. 1994 Non-linear pressure distribution in uniform microchannels. Appl. Microfabrication Fluid Mech. 197, 51–56.Google Scholar
Rathakrishnan, E. & Sreekanth, A. K. 1995 Rarefied flow through sudden enlargements. Fluid Dyn. Res. 16, 131–145.Google Scholar
Roohi, E. & Darbandi, M. 2009 Extending the Navier–Stokes solutions to transition regime in two-dimensional micro- and nanochannel flows using information preservation scheme. Phys. Fluids 21, 082001.Google Scholar
Sharipov, F. & Seleznev, V. 1998 Data on internal rarefied gas flows. J. Phys. Chem. Ref. Data 27 (3), 657–706.Google Scholar
Singh, N., Dongari, N. & Agrawal, A. 2013 Analytical solution of plane Poiseuille flow within Burnett hydrodynamics. Microfluid Nanofluid doi:10.1007/s 10404-013-1224-7.Google Scholar
Sisawath, S., Jing, X., Pain, C. C. & Zimmerman, R. W. 2002 Creeping flow through an axisymmetric sudden contraction or expansion. J. Fluids Engng 124, 273–278.Google Scholar
Sreekanth, A. K. 1969 Slip flow through long circular tubes. In Proceedings of the Sixth International Symposium on Rarefied Gas Dynamics (ed. Trilling, L. & Wachman, H. Y.), pp. 667–680. Academic.Google Scholar
Tsai, C. H., Chen, H. T., Wang, Y. N., Lin, C. H. & Fu, L. M. 2007 Capabilities and limitations of 2-dimensional and 3-dimensional numerical methods in modelling the fluid flow in sudden expansion microchannels. Microfluid Nanofluid 3, 13–18.Google Scholar
Verma, B., Demsis, A., Agrawal, A. & Prabhu, S. V. 2009 Semiempirical correlation for the friction factor of gas flowing through smooth microtubes. J. Vac. Sci. Technol. A 273, 584–590.Google Scholar
Vijayalakshmi, K., Anoop, K. B., Patel, H. E., Harikrishna, P. V., Sundararajan, T. & Das, S. K. 2009 Effects of compressibility and transition to turbulence on flow through microchannels. Intl J. Heat Mass Transfer 52, 2196–2204.CrossRefGoogle Scholar
Weng, C. I., Li, W. L. & Hwang, C. C. 1999 Gaseous flow in microtubes at arbitrary Knudsen numbers. Nanotechnology 10, 373–379.Google Scholar
Xue, H. & Chen, S. 2003 DSMC simulation of microscale backward-facing step flow. Microscale Thermophys. Engng 7, 69–86.Google Scholar
Yamaguchi, H., Hanawa, T., Yamamoto, O., Yu, M., Egami, Y. & Niimi, T. 2011 Experimental measurement on tangential momentum accommodation coefficient in a single microtube. Microfluid Nanofluid 11, 57–64.Google Scholar
Yang, C.-Y., Chen, C.-W, LIN, T.-Y. & Kandlikar, S. G. 2012 Heat transfer and friction characteristics of air flow in microtubes. Exp. Therm. Fluid Sci. 37, 12–18.Google Scholar
Zohar, Y., Lee, S. Y. K., Lee, W. Y., Jiang, L. & Tong, P. 2002 Subsonic gas flow in a straight and uniform microchannel. J. Fluid Mech. 472, 125–151.Google Scholar