Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-01-24T21:48:02.515Z Has data issue: false hasContentIssue false
  • English
  • Français

Bedforms in a turbulent stream: ripples, chevrons and antidunes

Published online by Cambridge University Press:  28 November 2011

Bruno Andreotti ,
Philippe Claudin ,
Olivier Devauchelle ,
Orencio Durán  and
Antoine Fourrière
Bruno Andreotti*
Affiliation:
Laboratoire de Physique et Mécanique des Milieux Hétérogènes (PMMH UMR 7636 ESPCI – CNRS – Univ. Paris Diderot – Univ. P. M. Curie), 10 rue Vauquelin, 75231, Paris CEDEX 05, France
Philippe Claudin
Affiliation:
Laboratoire de Physique et Mécanique des Milieux Hétérogènes (PMMH UMR 7636 ESPCI – CNRS – Univ. Paris Diderot – Univ. P. M. Curie), 10 rue Vauquelin, 75231, Paris CEDEX 05, France
Olivier Devauchelle
Affiliation:
Laboratoire de Physique et Mécanique des Milieux Hétérogènes (PMMH UMR 7636 ESPCI – CNRS – Univ. Paris Diderot – Univ. P. M. Curie), 10 rue Vauquelin, 75231, Paris CEDEX 05, France Department of Earth, Atmospheric and Planetary Sciences, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, MA 02139-4307, USA
Orencio Durán
Affiliation:
Laboratoire de Physique et Mécanique des Milieux Hétérogènes (PMMH UMR 7636 ESPCI – CNRS – Univ. Paris Diderot – Univ. P. M. Curie), 10 rue Vauquelin, 75231, Paris CEDEX 05, France
Antoine Fourrière
Affiliation:
Laboratoire de Physique et Mécanique des Milieux Hétérogènes (PMMH UMR 7636 ESPCI – CNRS – Univ. Paris Diderot – Univ. P. M. Curie), 10 rue Vauquelin, 75231, Paris CEDEX 05, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The interaction between a turbulent flow and a granular bed via sediment transport produces various bedforms associated with distinct hydrodynamical regimes. In this paper, we compare ripples (downstream-propagating transverse bedforms), chevrons and bars (bedforms inclined with respect to the flow direction) and antidunes (upstream-propagating bedforms), focusing on the mechanisms involved in the early stages of their formation. Performing the linear stability analysis of a flat bed, we study the asymptotic behaviours of the dispersion relation with respect to the physical parameters of the problem. 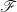In the subcritical regime (Froude number smaller than unity), we show that the same instability produces ripples or chevrons depending on the influence of the free surface. The transition from transverse to inclined bedforms is controlled by the ratio of the saturation length 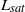, which encodes the stabilizing effect of sediment transport, to the flow depth 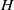, which determines the hydrodynamical regime. These results suggest that alternate bars form in rivers during flooding events, when suspended load dominates over bedload. In the supercritical regime 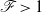, the transition from ripples to antidunes is also controlled by the ratio 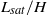. Antidunes appear around resonant conditions for free surface waves, a situation for which the sediment transport saturation becomes destabilizing. This resonance turns out to be fundamentally different from the inviscid prediction. Their wavelength selected by linear instability mostly scales on the flow depth 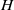, which is in agreement with existing experimental data. Our results also predict the emergence, at large Froude numbers, of ‘antichevrons’ or ‘antibars’, i.e. bedforms inclined with respect to the flow and propagating upstream.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Nonlinear Dynamical Systems: Pattern formation Geophysical and Geological Flows: River dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 690 , 10 January 2012 , pp. 94 - 128
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Alexander, J., Bridge, J. S., Cheel, R. J. & Leclair, S. F. 2001 Bedforms and associated sedimentary structures formed under supercritical water flows over aggrading sand beds. Sedimentology 48, 133–152.CrossRefGoogle Scholar
2. Andreotti, B., Claudin, P. & Douady, S. 2002 Selection of dune shapes and velocities. Part 2. A two-dimensional modelling. Eur. Phys. J. B 28, 341–352.CrossRefGoogle Scholar
3. Andreotti, B. & Claudin, C. 2007 Comment on ‘minimal size of a barchan dune’. Phys. Rev. E 76, 063301.CrossRefGoogle ScholarPubMed
4. Andreotti, B., Claudin, P. & Pouliquen, O. 2010 Measurements of the aeolian sand transport saturation length. Geomorphology 123, 343–348.CrossRefGoogle Scholar
5. Ashley, G. M. 1990 Classification of large scale subaqueous bedforms: a new look at an old problem. J. Sedim. Res. 60, 161–172.Google Scholar
6. Baas, J. H. 1994 A flume study on the development and equilibrium morphology of current ripples in very fine sand. Sedimentology 41, 185–209.CrossRefGoogle Scholar
7. Baas, J. H. 1999 An empirical model for the development and the equilibrium morphology of current ripples in fine sand. Sedimentology 46, 123–138.CrossRefGoogle Scholar
8. Bagnold, R. A. 1956 The flow of cohesionless grains in fluids. Phil. Trans. R. Soc. Lond. A 249, 235–297.Google Scholar
9. Callander, R. A. 1969 Instability and river channels. J. Fluid Mech. 36, 465–480.CrossRefGoogle Scholar
10. Carling, P. A. & Shvidchenko, A. B. 2002 A consideration of the dune: anti-dune transition in fine gravel. Sedimentology 49, 1269–1282.CrossRefGoogle Scholar
11. Chang, H. Y. & Simons, D. B. 1970 The bed configuration of straight sand-bed channels when flow is nearly critical. J. Fluid Mech. 42, 491–495.CrossRefGoogle Scholar
12. Chang, H. Y., Simons, D. B. & Woolhiser, D. A. 1971 Flume experiments on alternate bar formation. J. Waterways Harbors Coast. Eng. Div. 97, 155–165.CrossRefGoogle Scholar
13. Charru, F. 2006 Selection of the ripple length on a granular bed sheared by a liquid flow. Phys. Fluids 18, 121508.CrossRefGoogle Scholar
14. Chin, A. 1999 On the origin of step-pool sequences in mountain streams. Geophys. Res. Lett. 26, 231–234.CrossRefGoogle Scholar
15. Claudin, P., Charru, F. & Andreotti, B. 2011 Transport relaxation time and length scales in turbulent suspensions. J. Fluid Mech. 671, 491–506.CrossRefGoogle Scholar
16. Coleman, S. E. & Melville, B. W. 1994 Bed-form development. J. Hydraul. Engng 120, 544–560.CrossRefGoogle Scholar
17. Coleman, S. E. & Melville, B. W. 1996 Initiation of bed forms on a flat sand bed. J. Hydraul. Engng 122, 301–310.CrossRefGoogle Scholar
18. Coleman, S. E., Fedele, J. J. & Garcia, M. H. 2003 Closed-conduit bed-form initiation and development. J. Hydraul. Engng 129, 956–965.CrossRefGoogle Scholar
19. Colombini, M. 2004 Revisiting the linear theory of sand dune formation. J. Fluid Mech. 502, 1–16.CrossRefGoogle Scholar
20. Colombini, M. & Stocchino, A. 2005 Coupling or decoupling bed and flow dynamics: fast and slow sediment waves at high Froude numbers. Phys. Fluids 17, 036602.CrossRefGoogle Scholar
21. Colombini, M. & Stocchino, A. 2008 Finite-amplitude river dunes. J. Fluid Mech. 611, 283–306.CrossRefGoogle Scholar
22. Curran, J. C. 2007 Step-pool formation models and associated step spacing. Earth Surf. Process. Landf. 32, 1611–1627.CrossRefGoogle Scholar
23. Daerr, A., Lee, P., Lanuza, J. & Clément, E. 2003 Erosion patterns in a sediment layer. Phys. Rev. E 67, 065201(R).CrossRefGoogle Scholar
24. Devauchelle, O., Malverti, L., Lajeunesse, E., Josserand, C., Lagrée, P.-Y. & Métivier, F. 2010 Rhomboid beach pattern: a laboratory investigation. J. Geophys. Res. 115, F02017.Google Scholar
25. Devauchelle, O., Malverti, L., Lajeunesse, E., Lagrée, P.-Y., Josserand, C. & Nguyen Thu-Lam, K.-D. 2010 Stability of bedforms in laminar flows with free surface: from bars to ripples. J. Fluid Mech. 642, 329–348.CrossRefGoogle Scholar
26. Einstein, H. A. 1950 The bed load function for sedimentation in open channel flows. Technical Bulletin 1026, US Department of Agriculture, pp. 1–69.Google Scholar
27. Engelund, F. 1970 Instability of erodible beds. J. Fluid Mech. 42, 225–244.CrossRefGoogle Scholar
28. Engelund, F. & Fredsøe, J. 1982 Sediment ripples and dunes. Annu. Rev. Fluid Mech. 14, 13–37.CrossRefGoogle Scholar
29. Fernandez Luque, R. & van Beek, R. 1976 Erosion and transport of bed-load sediment. J. Hydraul Res. 14, 127–144.CrossRefGoogle Scholar
30. Fourrière, A., Claudin, P. & Andreotti, B. 2010 Bedforms in a turbulent stream: formation of ripples by primary linear instability and of dunes by nonlinear pattern coarsening. J. Fluid Mech. 649, 287–328.CrossRefGoogle Scholar
31. Fredsøe, J. 1978 Meandering and braiding of rivers. J. Fluid Mech. 84, 609–624.CrossRefGoogle Scholar
32. Fujita, Y. & Muramoto, Y. 1985 Studies on the process of development of alternate bars. Bull. Disas. Prev. Res. Inst. (Kyoto Univ.) 35, 55–86.Google Scholar
33. Gyr, A. & Schmid, A. 1989 The different ripple formation mechanism. J. Hydraul Res. 27, 61–74.CrossRefGoogle Scholar
34. Hayashi, T. 1970 Formation of dunes and anti-dunes in open channels. J. Hydraul. Div. 96, 357–366.CrossRefGoogle Scholar
35. Huang, L.-H. & Chiang, Y.-L. 2001 The formation of dunes, anti-dunes and rapidly damping waves in alluvial channels. Intl J. Numer. Anal. Meth. Geomech. 25, 675–690.CrossRefGoogle Scholar
36. Hunt, J. C. R., Leibovich, S. & Richards, K. J. 1988 Turbulent shear flows over low hills. Q. J. R. Meteorol. Soc. 114, 1435–1470.CrossRefGoogle Scholar
37. Ikeda, H. 1983 Experiments on bedload transport, bedforms, and sedimentary structures using fine gravel in the 4-meter-wide flume. Environ. Res. Center pap. (Tsukuba Univ.) 2, 1–78.Google Scholar
38. Ikeda, S. 1984 Prediction of alternate bar wavelength and height. J. Hydraul. Engng 110, 371–386.CrossRefGoogle Scholar
39. Izumi, N. & Parker, G. 1995 Inception of channelization and drainage basin formation: upstream-driven theory. J. Fluid Mech. 283, 341–363.CrossRefGoogle Scholar
40. Izumi, N. & Parker, G. 2000 Linear stability analysis of channel inception: downstream-driven theory. J. Fluid Mech. 419, 239–262.CrossRefGoogle Scholar
41. Jackson, P. S. & Hunt, J. C. R. 1975 Turbulent wind flow over a low hill. Q. J. R. Meteorol. Soc. 101, 929.CrossRefGoogle Scholar
42. Julien, P. Y. 1998 Erosion and Sedimentation. Cambridge University Press.Google Scholar
43. Karcz, I. & Kersey, D. 1980 Experimental study of free-surface flow instability and bedforms in shallow flows. Sedim. Geol. 27, 263–300.CrossRefGoogle Scholar
44. Kennedy, J. F. 1963 The mechanics of dunes and antidunes in erodible bed channels. J. Fluid Mech. 16, 521–544.CrossRefGoogle Scholar
45. Kostic, S., Sequeiros, O., Spinewine, B. & Parker, G. 2010 Cyclic steps: a phenomenon of supercritical shallow flow from the high mountains to the bottom of the ocean. J. Hydro-environment Res. 3, 167–172.CrossRefGoogle Scholar
46. Kubo, Y. & Yokokawa, M. 2001 Theoretical study on breaking of waves on anti-dunes. Spec. Publs. int. ass. sediment 31, 65–70.Google Scholar
47. Lajeunesse, E., Malverti, L. & Charru, F. 2010 Bedload transport in turbulent flow at the grain scale: experiments and modelling. J. Geophys. Res. 115, F04001.Google Scholar
48. Langlois, V. & Valance, A. 2007 Formation and evolution of current ripples on a flat sand bed under turbulent water flow. Eur. Phys. J. E 22, 201–208.CrossRefGoogle ScholarPubMed
49. Lanzoni, S. 2000a Experiments on bar formation in a straight flume. 1. Graded sediment. Water Resour. Res. 36, 3337–3349.CrossRefGoogle Scholar
50. Lanzoni, S. 2000b Experiments on bar formation in a straight flume. 2. Uniform sediment. Water Resour. Res. 36, 3351–3363.CrossRefGoogle Scholar
51. Lenzi, M. A. 2001 Step-pool evolution in the rio Cordon, northeastern Italy. Earth Surf. Process. Landf. 26, 991–1008.CrossRefGoogle Scholar
52. Lisle, T. E., Ikeda, H. & Iseya, F. 1991 Formation of stationary alternate bars in a steep channel with mixed-size sediment: a flume experiment. Earth Surf. Process. Landf. 16, 463–469.CrossRefGoogle Scholar
53. Lisle, T. E., Pizzuto, J. E., Ikeda, H., Iseya, F. & Kodama, Y. 1997 Evolution of a sediment wave in an experimental channel. Water Resour. Res. 33, 1971–1981.CrossRefGoogle Scholar
54. Mantz, P. A. 1978 Bedforms produced by fine, cohesionless, granular and flakey sediments under subcritical water flows. Sedimentology 25, 83–103.CrossRefGoogle Scholar
55. McLean, S. R. 1990 The stability of ripples and dunes. Earth-Sci. Rev. 29, 131–144.CrossRefGoogle Scholar
56. Meyer-Peter, E. & Müller, R. 1948 Formulas for bed load transport. Proc., 2nd Meeting, IAHR, Stockholm, Sweden, 39–64.Google Scholar
57. Morton, R. A. 1978 Large-scale rhomboid bed forms and sedimentary structures associated with hurricane washover. Sedimentology 25, 183–204.CrossRefGoogle Scholar
58. Parker, G. 1975 Sediment inertia as cause of river anti-dunes. J. Hydraul. Div. 101, 211–221.CrossRefGoogle Scholar
59. Parker, G. 1976 On the cause of characteristic scales of meandering and braiding in rivers. J. Fluid Mech. 76, 457–480.CrossRefGoogle Scholar
60. Parker, G. & Izumi, N. 2000 Purely erosional cyclic and solitary steps created by flow over a cohesive bed. J. Fluid Mech. 419, 203–238.CrossRefGoogle Scholar
61. Phillips, O. M. 1977 The Dynamics of the Upper Ocean. Cambridge University Press.Google Scholar
62. Raudkivi, A. J. 1966 Bedforms in alluvial channels. J. Fluid Mech. 26, 507–514.CrossRefGoogle Scholar
63. Raudkivi, A. J. 2006 Transition from Ripples to Dunes. J. Hydraul. Engng 132, 1316–1320.CrossRefGoogle Scholar
64. Raudkivi, A. J. & Witte, H. H. 1990 Development of Bed Features. J. Hydraul. Engng 116, 1063–1079.CrossRefGoogle Scholar
65. Rauen, W. B., Lin, B. & Falconer, R. A. 2008 Transition from wavelets to ripples in a laboratory flume with a diverging channel. Intl J. Sedim. Res. 23, 1–12.CrossRefGoogle Scholar
66. Partheniades, E. 1965 Erosion and deposition of cohesive soils. J. Hydraul. Div. 91, 105–139.CrossRefGoogle Scholar
67. Recking, A., Bacchi, V., Naaim, M. & Frey, P. 2009 Antidunes on steep slopes. J. Geophys. Res. 114, F04025.Google Scholar
68. Reynolds, A. J. 1965 Waves on the erodible bed of an open channel. J. Fluid Mech. 22, 113–133.CrossRefGoogle Scholar
69. Richards, K. J. 1980 The formation of ripples and dunes on an erodible bed. J. Fluid Mech. 99, 597–618.CrossRefGoogle Scholar
70. Robert, A. & Uhlman, W. 2001 An experimental study of the ripple-dune transition. Earth Surf. Process. Landforms 26, 615–629.CrossRefGoogle Scholar
71. van Rijn, L. C. 1984a Sediment pick-up functions. J. Hydraul. Engng 110, 1494–1502.CrossRefGoogle Scholar
72. van Rijn, L. C. 1984b Sediment transport, Part II: suspended load transport. J. Hydraul. Engng 110, 1613–1641.CrossRefGoogle Scholar
73. Rouse, H. 1936 Modern conceptions of the mechanics of fluid turbulence. Trans. ASCE 1965, 463–543.Google Scholar
74. Sauermann, G., Kroy, K. & Herrmann, H. J. 2001 Continuum saltation model for sand dunes. Phys. Rev. E 64, 031305.CrossRefGoogle ScholarPubMed
75. Schumm, S. A. & Khan, H. R. 1972 Experimental study of channel patterns. Geol. Soc. Am. Bull. 83, 1755–1770.CrossRefGoogle Scholar
76. Summer, B. M. & Bakioglu, M. 1984 On the formation of ripples on an erodible bed. J. Fluid Mech. 144, 177–190.CrossRefGoogle Scholar
77. Tubino, M., Repetto, R. & Zolezzi, G. 1999 Free bars in rivers. J. Hydraul Res. 37, 759–775.CrossRefGoogle Scholar
78. Vanoni, V. A. 1946 Transportation of suspended sediment by water. Trans. ASCE 111, 67–133.Google Scholar
79. Venditti, J. G., Church, M. A. & Bennett, S. J. 2005 Bed form initiation from a flat sand bed. J. Geophys. Res. 110, F01009.Google Scholar
80. Weichert, R. B., Bezzola, G. R. & Minor, H. -E. 2008 Bed morphology and generation of step-pool channels. Earth Surf. Process. Landf. 33, 1678–1692.CrossRefGoogle Scholar
81. Whittaker, J. G. & Jaeggi, M. 1982 Origin of step-pool systems in mountain streams. J. Hydraul. Div. 108, 758–773.CrossRefGoogle Scholar
82. Woodford, A. O. 1935 Rhomboid ripple mark. Am. J. Sci. 29, 518–525.CrossRefGoogle Scholar
Supplementary material: PDF

Andreotti et al. supplementary material

Supplementary material

Download Andreotti et al. supplementary material(PDF)
PDF 486.9 KB