Published online by Cambridge University Press: 18 July 2019
We consider two-dimensional quasi-geostrophic annular flows around a circular island with a radial offshore bottom slope. Since the conical bottom topography causes a certain beta effect, by analogy with the conventional beta plane we term our model a beta cone. Our focus is on the flows with zero total circulation, which are composed of two concentric rings of uniform potential vorticity (PV) attached to the island. The linear stability of such flows on a beta cone was investigated in a previous publication of ours. In the present paper, we study numerically the nonlinear evolution of weakly viscous flows, whose parameters are fitted so as to guarantee the highest instability of the azimuthal mode 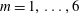 $m=1,\ldots ,6$. We study the production of vortices and Rossby waves due to the instability, consider the effect of waves on the emerging vortices and the interaction between the vortices. As in the flat-bottom case, at
$m=1,\ldots ,6$. We study the production of vortices and Rossby waves due to the instability, consider the effect of waves on the emerging vortices and the interaction between the vortices. As in the flat-bottom case, at 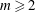 $m\geqslant 2$, the instability at weak bottom slopes normally leads to the emission of
$m\geqslant 2$, the instability at weak bottom slopes normally leads to the emission of 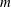 $m$ dipoles. However, a fundamental difference between the flat-bottom and beta-cone cases is observed in the trajectories of the dipoles as the latter recede from the island. When the flow is initially counterclockwise, the conical beta effect may force the dipoles to make a complete turn, come back to the island and rearrange in new couples that again leave the island and return. This quasi-periodic process gradually fades due to filamentation, wave radiation and viscous dissipation. Another possible outcome is symmetrical settling of
$m$ dipoles. However, a fundamental difference between the flat-bottom and beta-cone cases is observed in the trajectories of the dipoles as the latter recede from the island. When the flow is initially counterclockwise, the conical beta effect may force the dipoles to make a complete turn, come back to the island and rearrange in new couples that again leave the island and return. This quasi-periodic process gradually fades due to filamentation, wave radiation and viscous dissipation. Another possible outcome is symmetrical settling of 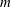 $m$ dipoles in a circular orbit around the island, in which they move counterclockwise. This behaviour is reminiscent of the adaptation of strongly tilted beta-plane modons (dipoles) to the eastward movement. If the initial flow is clockwise, the emerged dipoles usually disintegrate, but sometimes, the orbital arrangement is possible. At a moderate slope, the evolution of an unstable flow, which is initially clockwise, may end up in the formation of a counterclockwise flow. At steeper slopes, a clockwise flow may transform into a quasi-stationary vortex multipole. When the slope is sufficiently steep, the topographic Rossby waves developing outside of the PV rings can smooth away the instability crests and troughs at the outer edge of the main flow, thus preventing the vortex production but allowing the formation of a new quasi-stationary pattern, a doubly connected coherent PV structure possessing
$m$ dipoles in a circular orbit around the island, in which they move counterclockwise. This behaviour is reminiscent of the adaptation of strongly tilted beta-plane modons (dipoles) to the eastward movement. If the initial flow is clockwise, the emerged dipoles usually disintegrate, but sometimes, the orbital arrangement is possible. At a moderate slope, the evolution of an unstable flow, which is initially clockwise, may end up in the formation of a counterclockwise flow. At steeper slopes, a clockwise flow may transform into a quasi-stationary vortex multipole. When the slope is sufficiently steep, the topographic Rossby waves developing outside of the PV rings can smooth away the instability crests and troughs at the outer edge of the main flow, thus preventing the vortex production but allowing the formation of a new quasi-stationary pattern, a doubly connected coherent PV structure possessing 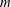 $m$-fold symmetry. Such an
$m$-fold symmetry. Such an 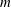 $m$-fold pattern can be steady only if it rotates counterclockwise, otherwise it radiates Rossby waves and transforms eventually into a circularly symmetric flow.
$m$-fold pattern can be steady only if it rotates counterclockwise, otherwise it radiates Rossby waves and transforms eventually into a circularly symmetric flow.