Published online by Cambridge University Press: 28 November 2018
Exact solutions for multipolar azimuthal-mode vortices in two-dimensional Euler flows are presented. Flow solutions with non-vanishing far-field velocity are provided for any set of azimuthal wavenumbers 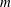 $m$ and arbitrary number
$m$ and arbitrary number  $n$ of vorticity shells. For azimuthal wavenumbers
$n$ of vorticity shells. For azimuthal wavenumbers 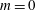 $m=0$ and
$m=0$ and 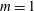 $m=1$, the far-field velocity is a rigid motion and unsteady flow solutions with vanishing far-field velocity are obtained by means of a time-dependent change of reference frame. Addition of these first two modes, in the case of
$m=1$, the far-field velocity is a rigid motion and unsteady flow solutions with vanishing far-field velocity are obtained by means of a time-dependent change of reference frame. Addition of these first two modes, in the case of 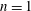 $n=1$, results in a particular Chaplygin–Lamb (C–L) dipole, with continuous and vanishing vorticity at the vortex boundary. Numerical simulations suggest that this particular C–L dipole is stable.
$n=1$, results in a particular Chaplygin–Lamb (C–L) dipole, with continuous and vanishing vorticity at the vortex boundary. Numerical simulations suggest that this particular C–L dipole is stable.