Published online by Cambridge University Press: 17 November 2020
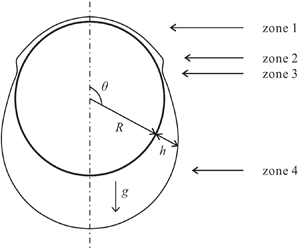
We study the axisymmetric evolution of a liquid film on a solid sphere governed by gravity, capillarity and viscous forces. The lubrication equations established in spherical coordinates are numerically solved using finite elements and local similarity solutions are obtained. Results show that the evolution behaves differently at early and late stages. At the early stage, the interface evolves in such a way that the capillary effect can be ignored. At the late stage, there emerge four zones from top to bottom: a thin film, a ridge ring, a dimple ring and a pendant drop. Each zone is governed by the balance of different forces, and hence is characterized by an individual physical mechanism. Consequently, the pendant drop is quasi-static, and the film thicknesses of other regions follow different scaling laws. The position of the dimple remains unchanged at the late stage.