Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-06T07:07:13.106Z Has data issue: false hasContentIssue false
  • English
  • Français

Axisymmetric, constantly supplied gravity currents at high Reynolds number

Published online by Cambridge University Press:  12 April 2011

ANJA C. SLIM  and
HERBERT E. HUPPERT
ANJA C. SLIM*
Affiliation:
Institute of Theoretical Geophysics, Department of Applied Mathematics and Theoretical Physics, Centre for Mathematical Sciences, University of Cambridge, Wilberforce Road, Cambridge, CB3 0WA, UK
HERBERT E. HUPPERT
Affiliation:
Institute of Theoretical Geophysics, Department of Applied Mathematics and Theoretical Physics, Centre for Mathematical Sciences, University of Cambridge, Wilberforce Road, Cambridge, CB3 0WA, UK
*
†Present address: Schlumberger-Doll Research, 1 Hampshire Street, Cambridge, MA 02139, USA. Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider theoretically the long-time evolution of axisymmetric, high Reynolds number, Boussinesq gravity currents supplied by a constant, small-area source of mass and radial momentum in a deep, quiescent ambient. We describe the gravity currents using a shallow-water model with a Froude number closure condition to incorporate ambient form drag at the front and present numerical and asymptotic solutions. The predicted profile consists of an expanding, radially decaying, steady interior that connects via a shock to a deeper, self-similar frontal boundary layer. Controlled by the balance of interior momentum flux and frontal buoyancy across the shock, the front advances as (g′sQ/r1/4s)4/15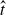4/5, where g′s is the reduced gravity of the source fluid, Q is the total volume flux, rs is the source radius and 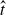is time. A radial momentum source has no effect on this solution below a non-zero threshold value. Above this value, the (virtual) radius over which the flow becomes critical can be used to collapse the solution onto the subthreshold one. We also use a simple parameterization to incorporate the effect of interfacial entrainment, and show that the profile can be substantially modified, although the buoyancy profile and radial extent are less significantly impacted. Our predicted profiles and extents are in reasonable agreement with existing experiments.

JFM classification

Geophysical and Geological Flows: Gravity currents
Type
Papers
Information
Journal of Fluid Mechanics , Volume 675 , 25 May 2011 , pp. 540 - 551
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Benjamin, T. B. 1968 Gravity currents and related phenomena. J. Fluid Mech. 31 (2), 209–248.Google Scholar
Britter, R. E. 1979 Spread of a negatively buoyant plume in a calm environment. Atmos. Environ. 13, 1241–1247.Google Scholar
Cenedese, C. & Adduce, C. 2010 A new parameterization for entrainment in overflows. J. Phys. Oceanogr. 40, 1835–1850.Google Scholar
Chen, J.-C. 1980 Studies on gravitational spreading currents. PhD thesis, California Institute of Technology.Google Scholar
Garvine, R. W. 1984 Radial spreading of buoyant, surface plumes in coastal waters. J. Geophys. Res. 89 (C2), 1989–1996.CrossRefGoogle Scholar
Gratton, J. & Vigo, C. 1994 Self-similar gravity currents with variable inflow revisited: plane currents. J. Fluid Mech. 258, 77–104.Google Scholar
Grundy, R. E. & Rottman, J. W. 1985 The approach to self-similarity of the solutions of the shallow-water equations representing gravity-current releases. J. Fluid Mech. 156, 39–53.Google Scholar
Hacker, J., Linden, P. F. & Dalziel, S. B. 1996 Mixing in lock-release gravity currents. Dyn. Atmos. Oceans 24, 183–195.Google Scholar
Hallworth, M. A., Huppert, H. E., Phillips, J. C. & Sparks, R. S. J. 1996 Entrainment into two-dimensional and axisymmetric turbulent gravity currents. J. Fluid Mech. 308, 289–311.Google Scholar
Huppert, H. E. 1982 The propagation of two-dimensional and axisymmetric viscous gravity currents over a rigid horizontal surface. J. Fluid Mech. 121, 43–58.Google Scholar
Ivey, G. N. & Blake, S. 1985 Axisymmetrical withdrawal and inflow in a density-stratified container. J. Fluid Mech. 161, 115–137.Google Scholar
Kaye, N. B. & Hunt, G. R. 2007 Overturning in a filling box. J. Fluid Mech. 576, 297–323.Google Scholar
Kevorkian, J. 1991 Partial Differential Equations: Analytical Solution Techniques. Springer.Google Scholar
Linden, P. F. & Simpson, J. E. 1994 Continuous releases of dense fluid from an elevated point source in a cross-flow. In Mixing and Transport in the Environment (ed. Beven, K. J., Chatwin, P. C. & Millbank, J. H.), pp. 401–418. Wiley.Google Scholar
Marino, B. M., Thomas, L. P. & Linden, P. F. 2005 The front condition for gravity currents. J. Fluid Mech. 536, 49–78.Google Scholar
O'Donnell, J. 1990 The formation and fate of a river plume; a numerical model. J. Phys. Oceanogr. 20, 551–569.Google Scholar
Patterson, M. D., Simpson, J. E., Dalziel, S. B. & van Heijst, G. J. F. 2006 Vortical motion in the head of an axisymmetric gravity current. Phys. Fluids 18, 046601.CrossRefGoogle Scholar
Simpson, J. E. 1997 Gravity Currents: In the Environment and the Laboratory, 2nd edn. Cambridge University Press.Google Scholar
Simpson, J. E. & Britter, R. E. 1980 A laboratory model of an atmospheric mesofront. Q. J. R. Meteorol. Soc. 106, 485–500.CrossRefGoogle Scholar
Slim, A. C. 2006 High Reynolds number gravity currents. PhD thesis, University of Cambridge.Google Scholar
Slim, A. C. & Huppert, H. E. 2008 Gravity currents from a line source in an ambient flow. J. Fluid Mech. 606, 1–26.Google Scholar
Turner, J. S. 1986 Turbulent entrainment: the development of the entrainment assumption and its applications to geophysical flows. J. Fluid Mech. 170, 431–471.Google Scholar
Ungarish, M. 2009 An Introduction to Gravity Currents and Intrusions. Chapman & Hall/CRC.Google Scholar
Wilkinson, D. L. & Wood, I. R. 1971 A rapidly varied flow phenomenon in a two-layer flow. J. Fluid Mech. 47 (02), 241–256.CrossRefGoogle Scholar