Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-23T09:21:47.145Z Has data issue: false hasContentIssue false
  • English
  • Français

Axial mixing and vortex stability to in situ radial injection in Taylor–Couette laminar and turbulent flows

Published online by Cambridge University Press:  19 September 2018

Nikolas A. Wilkinson Open the ORCID record for Nikolas A. Wilkinson [Opens in a new window]  and
Cari S. Dutcher Open the ORCID record for Cari S. Dutcher [Opens in a new window]
Nikolas A. Wilkinson
Affiliation:
Department of Chemical Engineering and Materials Science, University of Minnesota – Twin Cities, 421 Washington Avenue SE, Minneapolis, MN 55455, USA
Cari S. Dutcher*
Affiliation:
Department of Mechanical Engineering, University of Minnesota – Twin Cities, 111 Church Street SE, Minneapolis, MN 55455, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Taylor–Couette flows have been widely studied in part due to the enhanced mixing performance from the variety of hydrodynamic flow states accessible. These process improvements have been demonstrated despite the traditionally limited injection mechanisms from the complexity of the Taylor–Couette geometry. In this study, using a newly designed, modified Taylor–Couette cell, axial mass transport behaviour is experimentally determined over two orders of magnitude of Reynolds number. Four different flow states, including laminar and turbulent Taylor vortex flows and laminar and turbulent wavy vortex flows, were studied. Using flow visualization techniques, the measured dispersion coefficient was found to increase with increasing 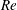$Re$, and a single, unified regression is found for all vortices studied. In addition to mass transport, the vortex structures’ stability to radial injection is also quantified. A dimensionless stability criterion, the ratio of injection to diffusion time scales, was found to capture the conditions under which vortex structures are stable to injection. Using the stability criterion, global and transitional stability regions are identified as a function of Reynolds number, 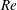$Re$.

JFM classification

Mixing: Chaotic advection Flow Control: Mixing enhancement Vortex Flows: Vortex dynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 854 , 10 November 2018 , pp. 324 - 347
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahmad, A. L., Kusumastuti, A., Shah Buddin, M. M. H., Derek, C. J. C. & Ooi, B. S. 2014 Emulsion liquid membrane based on a new flow pattern in a counter rotating Taylor–Couette column for cadmium extraction. Sep. Purif. Technol. 127, 46–52.Google Scholar
Andereck, C. D., Liu, S. S. & Swinney, H. L. 1986 Flow regimes in a circular Couette system with independently rotating cylinders. J. Fluid Mech. 164 (1), 155–183.Google Scholar
Baier, G. & Graham, M. D. 2000 Two-fluid Taylor–Couette flow with countercurrent axial flow: linear theory for immiscible liquids between corotating cylinders. Phys. Fluids 12 (2), 294–303.Google Scholar
Beaudoin, G. & Jaffrin, M. Y. 1989 Plasma filtration in Couette flow membrane devices. Artif. Organs 13 (1), 43–51.Google Scholar
van den Berg, T., Doering, C., Lohse, D. & Lathrop, D. 2003 Smooth and rough boundaries in turbulent Taylor–Couette flow. Phys. Rev. E 68 (3), 036307.Google Scholar
Coles, D. 1965 Transition in circular Couette flow. J. Fluid Mech. 21 (3), 385–425.Google Scholar
Coufort, C., Bouyer, D. & Liné, A. 2005 Flocculation related to local hydrodynamics in a Taylor–Couette reactor and in a jar. Chem. Engng Sci. 60 (8–9), 2179–2192.Google Scholar
Dubrulle, B., Dauchot, O., Daviaud, F., Longaretti, P.-Y., Richard, D. & Zahn, J.-P. 2005 Stability and turbulent transport in Taylor–Couette flow from analysis of experimental data. Phys. Fluids 17 (9), 095103.Google Scholar
Dusting, J. & Balabani, S. 2009 Mixing in a Taylor–Couette reactor in the non-wavy flow regime. Chem. Engng Sci. 64 (13), 3103–3111.Google Scholar
Dutcher, C. S. & Muller, S. J. 2007 Explicit analytic formulas for Newtonian Taylor–Couette primary instabilities. Phys. Rev. E 75 (4 Pt 2), 047301.Google Scholar
Dutcher, C. S. & Muller, S. J. 2009 Spatio-temporal mode dynamics and higher order transitions in high aspect ratio Newtonian Taylor–Couette flows. J. Fluid Mech. 641, 85–113.Google Scholar
Dutcher, C. S. & Muller, S. J. 2011 Effects of weak elasticity on the stability of high Reynolds number co- and counter-rotating Taylor–Couette flows. J. Rheol. 55 (6), 1271–1295.Google Scholar
Dutta, P. K. & Ray, A. K. 2004 Experimental investigation of Taylor vortex photocatalytic reactor for water purification. Chem. Engng Sci. 59 (22–23), 5249–5259.Google Scholar
Eckhardt, B., Grossmann, S. & Lohse, D. 2007 Torque scaling in turbulent Taylor–Couette flow between independently rotating cylinders. J. Fluid Mech. 581, 221–250.Google Scholar
Fardin, M. A., Perge, C. & Taberlet, N. 2014 The hydrogen atom of fluid dynamics: introduction to the Taylor–Couette flow for soft matter scientists. Soft Matt. 10 (20), 3523–3535.Google Scholar
Haut, B., Ben Amor, H., Coulon, L., Jacquet, A. & Halloin, V. 2003 Hydrodynamics and mass transfer in a Couette–Taylor bioreactor for the culture of animal cells. Chem. Engng Sci. 58 (3–6), 777–784.Google Scholar
Kataoka, K., Ohmura, N., Kouzu, M., Simamura, Y. & Okubo, M. 1995 Emulsion polymerization of styrene in a continuous Taylor vortex flow reactor. Chem. Engng Sci. 50 (9), 1409–1416.Google Scholar
Kataoka, K. & Takigawa, T. 1981 Intermixing over cell boundary between Taylor vortices. AIChE J. 27 (3), 504–508.Google Scholar
Kim, M., Park, K. J., Lee, K. U., Kim, M. J., Kim, W.-S., Kwon, O. J. & Kim, J. J. 2014 Preparation of black pigment with the Couette–Taylor vortex for electrophoretic displays. Chem. Engng Sci. 119, 245–250.Google Scholar
Krintiras, G. A., Gadea Diaz, J., van der Goot, A. J., Stankiewicz, A. I. & Stefanidis, G. D. 2016 On the use of the Couette Cell technology for large scale production of textured soy-based meat replacers. J. Food Engng 169, 205–213.Google Scholar
Nemri, M., Cazin, S., Charton, S. & Climent, E. 2014 Experimental investigation of mixing and axial dispersion in Taylor–Couette flow patterns. Exp. Fluids 55 (7), 1769–1784.Google Scholar
Nemri, M., Charton, S. & Climent, E. 2016 Mixing and axial dispersion in Taylor–Couette flows: the effect of the flow regime. Chem. Engng Sci. 139, 109–124.Google Scholar
Nemri, M., Climent, E., Charton, S., Lanoë, J.-Y. & Ode, D. 2013 Experimental and numerical investigation on mixing and axial dispersion in Taylor–Couette flow patterns. Chem. Engng Res. Des. 91 (12), 2346–2354.Google Scholar
Ohmura, N., Kataoka, K., Shibata, Y. & Makino, T. 1997 Effective mass diffusion over cell boundaries in a Taylor–Couette flow system. Chem. Engng Sci. 52 (11), 1757–1765.Google Scholar
Ohmura, N., Makino, T., Motomura, A., Shibata, Y. & Kataoka, K. 1998 Intercellular mass transfer in wavy/turbulent Taylor vortex flow. Intl J. Heat Fluid Flow 19 (2), 159–166.Google Scholar
Park, Y., Forney, L. J., Kim, J. H. & Skelland, A. H. P. 2004 Optimum emulsion liquid membranes stabilized by non-Newtonian conversion in Taylor–Couette flow. Chem. Engng Sci. 59 (24), 5725–5734.Google Scholar
Ramezani, M., Kong, B., Gao, X., Olsen, M. G. & Vigil, R. D. 2015 Experimental measurement of oxygen mass transfer and bubble size distribution in an air–water multiphase Taylor–Couette vortex bioreactor. Chem. Engng J. 279, 286–296.Google Scholar
Sczechowski, J. G., Koval, C. A. & Noble, R. D. 1995 A Taylor vortex reactor for heterogeneous photocatalysis. Chem. Engng Sci. 50 (20), 3163–3173.Google Scholar
Taylor, G. I. 1923 Stability of a viscous liquid contained between two rotating cylinders. Phil. Trans. R. Soc. Lond. A 223, 289–343.Google Scholar
Wilkinson, N. & Dutcher, C. S. 2017 Taylor–Couette flow with radial fluid injection. Rev. Sci. Instrum. 88 (8), 083904.Google Scholar
Supplementary material: PDF

Wilkinson et al. Supplementary Material

Supplementary Figures 1-10

Download Wilkinson et al. Supplementary Material(PDF)
PDF 6.6 MB