Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-26T18:08:52.207Z Has data issue: false hasContentIssue false
  • English
  • Français

Axial evolution of forced helical flame and flow disturbances

Published online by Cambridge University Press:  05 April 2018

Travis E. Smith Open the ORCID record for Travis E. Smith [Opens in a new window] ,
Christopher M. Douglas ,
Benjamin L. Emerson  and
Timothy C. Lieuwen
Travis E. Smith
Affiliation:
Department of Aerospace Engineering, Georgia Institute of Technology, North Avenue, Atlanta, GA 30332, USA
Christopher M. Douglas
Affiliation:
Department of Mechanical Engineering, Georgia Institute of Technology, North Avenue, Atlanta, GA 30332, USA
Benjamin L. Emerson
Affiliation:
Department of Aerospace Engineering, Georgia Institute of Technology, North Avenue, Atlanta, GA 30332, USA
Timothy C. Lieuwen*
Affiliation:
Department of Aerospace Engineering, Georgia Institute of Technology, North Avenue, Atlanta, GA 30332, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper presents 5 kHz stereo particle image velocimetry and OH planar laser induced fluorescence measurements of transversely forced swirl flames. The presence of transverse forcing on this naturally unstable flow both influences the natural instabilities, as well as amplifies disturbances that may not necessarily manifest themselves during natural oscillations. By manipulating the structure of the acoustic forcing field, both axisymmetric and helical modes are preferentially excited away from the frequency of natural instability. The paper presents a method for spatially interpolating the phase locked 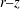$r{-}z$ and 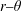$r{-}\unicode[STIX]{x1D703}$ planar velocity and flame position data, extracting the full three-dimensional structure of the helical disturbances. These helical disturbances are also decomposed into symmetric and anti-symmetric disturbances about the jet core, showing the subsequent axial evolution (in magnitude and phase) of each of these underlying disturbances. It is shown that out-of-phase acoustic forcing excites 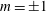$m=\pm 1$ modes, but the flow field preferentially amplifies the counter-winding, co-rotating helical disturbance over the co-winding, counter-rotating helical disturbance. This causes the flow and flame to transition from a transverse flapping near the jet exit to a precessing motion further downstream. In contrast, in-phase forcing promotes axisymmetric 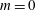$m=0$ disturbances which dominate the flow field over the entire axial domain. In both cases, the amplitudes of the anti-symmetric disturbances about the jet core grow with downstream distance before saturating and decaying, while the symmetric disturbances appear nearly negligible. It is suggested that this saturation and decay is due to linear effects (e.g. a negative spatial growth rate), rather than nonlinear interactions.

JFM classification

Instability: Absolute/convective instability Reacting Flows: Combustion Reacting Flows: Reacting Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 844 , 10 June 2018 , pp. 323 - 356
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acharya, V. S., Shin, D. H. & Lieuwen, T. 2013 Premixed flames excited by helical disturbances: flame wrinkling and heat release oscillations. J. Propul. Power 29, 1282–1291.10.2514/1.B34883Google Scholar
Aguilar, M., Malanoski, M., Adhitya, G., Emerson, B., Acharya, V., Noble, D. & Lieuwen, T. 2015 Helical flow disturbances in a multinozzle combustor. Trans. ASME J. Engng Gas Turbines Power 137 (9), 091507.10.1115/1.4029696Google Scholar
Arndt, C., Steinberg, A., Boxx, I., Meier, W., Aigner, M. & Carter, C. 2010 Flow-field and flame dynamics of a gas turbine model combustor during transition between thermo-acoustically stable and unstable states. In Turbo Expo. ASME.Google Scholar
Billant, P., Chomaz, J. M. & Huerre, P. 1998 Experimental study of vortex breakdown in swirling jets. J. Fluid Mech. 376, 183–219.10.1017/S0022112098002870Google Scholar
Blimbaum, J., Zanchetta, M., Akin, T., Acharya, V., O’Connor, J., Noble, D. R. & Lieuwen, T. 2012 Transverse to longitudinal acoustic coupling processes in annular combustion chambers. Intl J. Spray Combust. Dyn. 4, 275–297.10.1260/1756-8277.4.4.275Google Scholar
Cohen, J. & Wygnanski, I. 1987 The evolution of instabilities in the axisymmetric jet. Part 2. The flow resulting from the interaction between two waves. J. Fluid Mech. 176, 221–235.10.1017/S0022112087000636Google Scholar
Day, M., Tachibana, S., Bell, J., Lijewski, M., Beckner, V. & Cheng, R. K. 2012 A combined computational and experimental characterization of lean premixed turbulent low swirl laboratory flames: I. Methane flames. Combust. Flame 159, 275–290.10.1016/j.combustflame.2011.06.016Google Scholar
Faler, J. H. & Leibovich, S. 1977 Disrupted states of vortex flow and vortex breakdown. Phys. Fluids 20, 1385–1400.10.1063/1.862033Google Scholar
Fanaca, D., Alemela, P. R., Hirsch, C. & Sattelmayer, T. 2010 Comparison of the flow field of a swirl stabilized premixed burner in an annular and a single burner combustion chamber. Engng Gas Turbines Power 132 (7), 071502.Google Scholar
Gaster, M. 1962 A note on the relation between temporally-increasing and spatially-increasing disturbances in hydrodynamic stability. J. Fluid Mech. 14, 222–224.10.1017/S0022112062001184Google Scholar
Ghirardo, G. & Juniper, M. P. 2013 Azimuthal instabilities in annular combustors: standing and spinning modes. Proc. R. Soc. Lond. A 469 (2157), 20130232.10.1098/rspa.2013.0232Google Scholar
Gupta, A. K., Lilley, D. G. & Syred, N. 1984 Swirl Flows. Abacus Press.Google Scholar
Hauser, M., Lorenz, M. & Sattelmayer, T. 2011 Influence of transversal acoustic excitation of the burner approach flow on the flame structure. Trans. ASME J. Engng Gas Turbines Power 133, 041501.Google Scholar
Howard, L. N. & Gupta, A. S. 1962 On the hydrodynamic and hydromagnetic stability of swirling flows. J. Fluid Mech. 14, 463–476.10.1017/S0022112062001366Google Scholar
Huang, Y., Wang, S. W. & Yang, V. 2006 Systematic analysis of lean-premixed swirl-stabilized combustion. AIAA J. 44, 724–740.10.2514/1.15382Google Scholar
Huang, Y. & Yang, V. 2009 Dynamics and stability of lean-premixed swirl-stabilized combustion. Prog. Energy Combust. Sci. 35, 293–364.10.1016/j.pecs.2009.01.002Google Scholar
Juniper, M. P. 2012 Absolute and convective instability in gas turbine fuel injectors. In Proceedings of ASME Turbo Expo 2012.Google Scholar
Juniper, M. P., Tammisola, O. L. & Lundell, F. 2011 The local and global stability of confined planar wakes at intermediate Reynolds number. J. Fluid Mech. 686, 218–238.10.1017/jfm.2011.324Google Scholar
Kashinath, K., Hemchandra, S. & Juniper, M. P. 2013 Nonlinear thermoacoustics of ducted premixed flames: the influence of perturbation convection speed. Combust. Flame 160, 2856–2865.10.1016/j.combustflame.2013.06.019Google Scholar
Lacarelle, A., Faustmann, T., Greenblatt, D., Paschereit, C. O., Lehmann, O., Luchtenburg, D. M. & Noack, B. R. 2009 Spatiotemporal characterization of a conical swirler flow field under strong forcing. Trans. ASME J. Engng Gas Turbines Power 131 (3), 031504.10.1115/1.2982139Google Scholar
Liang, H. Z. & Maxworthy, T. 2005 An experimental investigation of swirling jets. J. Fluid Mech. 525, 115–159.10.1017/S0022112004002629Google Scholar
Lieuwen, T. 2012 Unsteady Combustor Physics. Cambridge University Press.10.1017/CBO9781139059961Google Scholar
Long, T. A. & Petersen, R. A. 1992 Controlled interactions in a forced axisymmetric jet. Part 1. The distortion of the mean flow. J. Fluid Mech. 235, 37–55.10.1017/S0022112092001010Google Scholar
Malanoski, M., Aguilar, M., Shin, D. H. & Lieuwen, T. 2014 Flame leading edge and flow dynamics in a swirling, lifted flame. Combust. Sci. Technol. 186, 1816–1843.10.1080/00102202.2014.923410Google Scholar
Manoharan, K., Emerson, B., Smith, T. E., Douglas, C. M., Lieuwen, T. & Hemchandra, S. 2017 Velocity field response of a forced swirl stabilized premixed flame. In ASME Turbo Expo 2017: Turbine Technical Conference and Exposition.Google Scholar
Manoharan, K., Hansford, S., O’Connor, J. & Hemchandra, S. 2015 Instability mechanism in a swirl flow combustor: precession of vortex core and influence of density gradient. In ASME Turbo Expo 2015: Turbine Technical Conference and Exposition.Google Scholar
O’Connor, J., Acharya, V. & Lieuwen, T. 2015 Transverse combustion instabilities: acoustics, hydrodynamics, and flame dynamics. Prog. Energy Combust. Sci. 49, 1–39.10.1016/j.pecs.2015.01.001Google Scholar
O’Connor, J. & Lieuwen, T. 2012a Further characterization of the disturbance field in a transversely excited swirl-stabilized flame. Trans. ASME J. Engng Gas Turbines Power 134 (1), 011501.10.1115/1.4004186Google Scholar
O’Connor, J. & Lieuwen, T. 2012b Recirculation zone dynamics of a transversely excited swirl flow and flame. Phys. Fluids 24 (7), 2893–2900.10.1063/1.4731300Google Scholar
Oberleithner, K., Paschereit, C. O. & Wygnanski, I. 2014 On the impact of swirl on the growth of coherent structures. J. Fluid Mech. 741, 156–199.10.1017/jfm.2013.669Google Scholar
Oberleithner, K., Schimek, S. & Paschereit, C. O. 2015 Shear flow instabilities in swirl-stabilized combustors and their impact on the amplitude dependent flame response: a linear stability analysis. Combust. Flame 162, 86–99.10.1016/j.combustflame.2014.07.012Google Scholar
Oberleithner, K., Sieber, M., Nayeri, C. N., Paschereit, C. O., Petz, C., Hege, H.-C., Noack, B. R. & Wygnanski, I. 2011 Three-dimensional coherent structures in a swirling jet undergoing vortex breakdown: stability analysis and empirical mode construction. J. Fluid Mech. 679, 383–414.10.1017/jfm.2011.141Google Scholar
Qadri, U. A., Mistry, D. & Juniper, M. P. 2013 Structural sensitivity of spiral vortex breakdown. J. Fluid Mech. 720, 558–581.10.1017/jfm.2013.34Google Scholar
Rosa, A. J. D., Samarasinghe, J., Peluso, S. J., Quay, B. D. & Santavicca, D. A. 2016 Flame area fluctuation measurements in velocity-forced premixed gas turbine flames. Trans. ASME J. Engng Gas Turbines Power 138 (4), 041507.Google Scholar
Roy, S., Yi, T., Jiang, N., Gunaratne, G. H., Chterev, I., Emerson, B., Lieuwen, T., Caswell, A. W. & Gord, J. R. 2017 Dynamics of robust structures in turbulent swirling reacting flows. J. Fluid Mech. 816, 554–585.10.1017/jfm.2017.71Google Scholar
Rukes, L., Sieber, M., Paschereit, C. O. & Oberleithner, K. 2016 The impact of heating the breakdown bubble on the global mode of a swirling jet: experiments and linear stability analysis. Phys. Fluids 28 (10), 104102.10.1063/1.4963274Google Scholar
Rusak, Z., Wang, S., Xu, L. & Taylor, S. 2012 On the global nonlinear stability of a near-critical swirling flow in a long finite-length pipe and the path to vortex breakdown. J. Fluid Mech. 712, 295–326.10.1017/jfm.2012.420Google Scholar
Smith, T. E., Emerson, B., Proscia, W. & Lieuwen, T. 2018 Role of induced axial acoustics in transverse acoustic flame response. Combust. Flame; (in press).10.1016/j.combustflame.2017.12.035Google Scholar
Soria, J. 1996 An investigation of the near wake of a circular cylinder using a video-based digital cross-correlation particle image velocimetry technique. Exp. Therm. Fluid Sci. 12, 221–233.10.1016/0894-1777(95)00086-0Google Scholar
Steinberg, A., Boxx, I., Stöhr, M., Meier, W. & Carter, C. 2012 Effects of flow structure dynamics on thermoacoustic instabilities in swirl-stabilized combustion. AIAA J. 50 (4), 952–967.10.2514/1.J051466Google Scholar
Steinberg, A. M., Arndt, C. M. & Meier, W. 2013 Parametric study of vortex structures and their dynamics in swirl-stabilized combustion. Proc. Combust. Inst. 34 (2), 3117–3125.10.1016/j.proci.2012.05.015Google Scholar
Syred, N. 2006 A review of oscillation mechanisms and the role of the precessing vortex core (pvc) in swirl combustion systems. Prog. Energy Combust. Sci. 32, 93–161.10.1016/j.pecs.2005.10.002Google Scholar
Tammisola, O. & Juniper, M. P. 2016 Coherent structures in a swirl injector at Re = 4800 by nonlinear simulations and linear global modes. J. Fluid Mech. 792, 620–657.10.1017/jfm.2016.86Google Scholar
Terhaar, S., Cosic, B., Oliver Paschereit, C. & Oberleithner, K. 2014 Impact of shear flow instabilities on the magnitude and saturation of the flame response. Trans. ASME J. Engng Gas Turbines Power 136, 071502.Google Scholar
Umeh, C. O. U., Rusak, Z. & Gutmark, E. 2012 Vortex breakdown in a swirl-stabilized combustor. J. Propul. Power 28, 1037–1051.10.2514/1.B34377Google Scholar
Wang, S. & Rusak, Z. 1996 On the stability of non-columnar swirling flows. Phys. Fluids 8, 1017–1023.10.1063/1.868878Google Scholar
Wang, S. X., Rusak, Z., Gong, R. & Liu, F. 2016 On the three-dimensional stability of a solid-body rotation flow in a finite-length rotating pipe. J. Fluid Mech. 797, 284–321.10.1017/jfm.2016.223Google Scholar
Willert, C. E. & Gharib, M. 1991 Digital particle image velocimetry. Exp. Fluids 10, 181–193.10.1007/BF00190388Google Scholar
Worth, N. A. & Dawson, J. R. 2013a Modal dynamics of self-excited azimuthal instabilities in an annular combustion chamber. Combust. Flame 160, 2476–2489.10.1016/j.combustflame.2013.04.031Google Scholar
Worth, N. A. & Dawson, J. R. 2013b Self-excited circumferential instabilities in a model annular gas turbine combustor: global flame dynamics. Proc. Combust. Inst. 34 (2), 3127–3134.10.1016/j.proci.2012.05.061Google Scholar