Hostname: page-component-848d4c4894-nmvwc Total loading time: 0 Render date: 2024-07-07T23:29:25.317Z Has data issue: false hasContentIssue false
  • English
  • Français

Attachment-line, cross-flow and Tollmien–Schlichting instabilities on swept ONERA-D and Joukowski airfoils

Published online by Cambridge University Press:  23 February 2023

Euryale Kitzinger Open the ORCID record for Euryale Kitzinger [Opens in a new window] ,
Tristan Leclercq Open the ORCID record for Tristan Leclercq [Opens in a new window] ,
Olivier Marquet Open the ORCID record for Olivier Marquet [Opens in a new window] ,
Estelle Piot  and
Denis Sipp Open the ORCID record for Denis Sipp [Opens in a new window]
Euryale Kitzinger*
Affiliation:
DAAA, ONERA, University of Paris-Saclay, F-92190 Meudon, France
Tristan Leclercq
Affiliation:
DAAA, ONERA, University of Paris-Saclay, F-92190 Meudon, France
Olivier Marquet
Affiliation:
DAAA, ONERA, University of Paris-Saclay, F-92190 Meudon, France
Estelle Piot
Affiliation:
ONERA/DMPE, University of Toulouse, F-31055 Toulouse, France
Denis Sipp
Affiliation:
DAAA, ONERA, University of Paris-Saclay, F-92190 Meudon, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

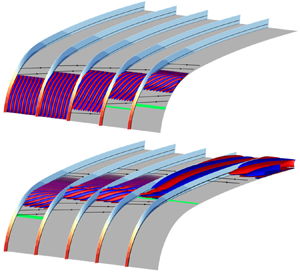
Linear stability analyses are performed to investigate the boundary layer instabilities developing in an incompressible flow around the whole leading-edge of swept ONERA-D and Joukowski airfoils of infinite span. The stability analyses conducted in our study are global in the chordwise direction and local in the spanwise direction. A neutral curve is drawn at a given leading-edge Reynolds number $Re_R$ and several overlapping regions, called ‘lobes’, are identified on a physical basis. A detailed study of the marginal modes reveals the presence of attachment-line and cross-flow instabilities, as well as modes whose features do not fall within the standards of a specific type. Connected cross-flow/Tollmien–Schlichting modes, that show a dominant spatial structure reminiscent of Tollmien–Schlichting waves but whose destabilization is linked to a cross-flow mechanism, have been identified. The comparison of several neutral curves at different $Re_R$ values reveals the greater stabilizing effect of the increase of $Re_R$ on the cross-flow instability compared with the attachment-line instability. The influence of the airfoil shape is also studied by comparing the neutral curves of the ONERA-D with the neutral curves of the Joukowski airfoil. These curves reveal similar characteristics with the presence of distinct lobes and their comparison at constant sweep angle shows that, under the conditions studied, the ONERA-D airfoil is more stable than the Joukowski airfoil, even for cross-flow instabilities. The absolutely or convectively unstable nature of the flow in the spanwise direction is also tackled and our results suggest that the flow is only convectively unstable.

JFM classification

Boundary Layers: Boundary layer stability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 957 , 25 February 2023 , A29
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahmed, N. & Rubino, S. 2019 Numerical comparisons of finite element stabilized methods for a 2D vortex dynamics simulation at high Reynolds number. Comput. Meth. Appl. Mech. Engng 349, 191–212.CrossRefGoogle Scholar
Alizard, F. & Robinet, J.-C. 2007 Spatially convective global modes in a boundary layer. Phys. Fluids 19 (11), 114105.CrossRefGoogle Scholar
Amestoy, P., Duff, I., L'Excellent, J.-Y. & Koster, J. 2001 A fully asynchronous multifrontal solver using distributed dynamic scheduling. SIAM J. Matrix Anal. Applics 23 (1), 15–41.CrossRefGoogle Scholar
Arnal, D. & Casalis, G. 2000 Laminar-turbulent transition prediction in three-dimensional flows. Prog. Aerosp. Sci. 36 (2), 173–191.CrossRefGoogle Scholar
Bertolotti, F. 2000 On the connection between cross-flow vortices and attachment-line instabilities. In Laminar-Turbulent Transition: IUTAM Symposium, Sedona, AZ, pp. 625–630. Springer.Google Scholar
Brynjell-Rahkola, M., Shahriari, N., Schlatter, P., Hanifi, A. & Henningson, D.S. 2017 Stability and sensitivity of a cross-flow-dominated Falkner–Skan–Cooke boundary layer with discrete surface roughness. J. Fluid Mech. 826, 830–850.CrossRefGoogle Scholar
Cerqueira, S. & Sipp, D. 2014 Eigenvalue sensitivity, singular values and discrete frequency selection mechanism in noise amplifiers: the case of flow induced by radial wall injection. J. Fluid Mech. 757, 770–799.CrossRefGoogle Scholar
Franca, L.P., Frey, S.L. & Hughes, T.J.R. 1992 Stabilized finite element methods: I. Application to the advective-diffusive model. Comput. Meth. Appl. Mech. Engng 95 (2), 253–276.CrossRefGoogle Scholar
Garnaud, X., Lesshafft, L., Schmid, P.J. & Huerre, P. 2013 Modal and transient dynamics of jet flows. Phys. Fluids 25 (4), 044103.CrossRefGoogle Scholar
Gianetti, F. & Luchini, P. 2007 Structural sensitivity of the first instability of the cylinder wake. J. Fluid Mech. 581, 167–197.CrossRefGoogle Scholar
Hall, P., Malik, M. & Poll, I. 1984 On the stability of an infinite swept attachment line boundary layer. Proc. R. Soc. Lond. A 395, 229–245.Google Scholar
Hall, P. & Seddougui, S. 1990 Wave interactions in a three-dimensional attachment-line boundary layer. J. Fluid Mech. 217, 367–390.CrossRefGoogle Scholar
Hecht, F. 2012 New development in FreeFem$++$. J. Numer. Maths 20 (3–4), 1–14.Google Scholar
Hernandez, V., Roman, J. & Vidal, V. 2005 SLEPc: a scalable and flexible toolkit for the solution of eigenvalue problems. ACM Trans. Math. Softw. 31 (3), 351–362.CrossRefGoogle Scholar
Houdeville, R. 1992 Three-dimensional boundary layer calculation by a characteristic method. In Fifth Symposium on Numerical and Physical Aspects of Aerodynamic Flows, Long Beach, CA, USA. NTRS - NASA.Google Scholar
Huerre, P. 2000 Open shear flow instabilities. In Perspectives in Fluid Dynamics (ed. G.K. Batchelor, H.K. Moffatt & M.G. Worster), pp. 159–229. Cambridge University Press.Google Scholar
Huerre, P. & Monkewitz, P. 1990 Local and global instabilities in spatially developing flows. Annu. Rev. Fluid Mech. 22 (1), 473–537.CrossRefGoogle Scholar
Joslin, R.D. 1996 Simulation of three-dimensional symmetric and asymmetric instabilities in attachment-line boundary layers. AIAA J. 34 (11), 2432–2434.CrossRefGoogle Scholar
Lin, R.-S. & Malik, M. 1996 On the stability of attachment-line boundary layers. Part 1. The incompressible swept Hiemenz flow. J. Fluid Mech. 311, 239–255.CrossRefGoogle Scholar
Lin, R.-S. & Malik, M. 1997 On the stability of attachment-line boundary layers. Part 2. The effect of leading-edge curvature. J. Fluid Mech. 333, 125–137.CrossRefGoogle Scholar
Lingwood, R. 1997 On the impulse response for swept boundary-layer flows. J. Fluid Mech. 344, 317–334.CrossRefGoogle Scholar
Mack, C. & Schmid, P. 2011 Global stability of swept flow around a parabolic body: the neutral curve. J. Fluid Mech. 678, 589–599.CrossRefGoogle Scholar
Mack, C., Schmid, P. & Sesterhenn, J. 2008 Global stability of swept flow around a parabolic body: connecting attachment-line and crossflow modes. J. Fluid Mech. 611, 205–214.CrossRefGoogle Scholar
Meliga, P., Sipp, D. & Chomaz, J.-M. 2008 Absolute instability in axisymmetric wakes: compressible and density variation effects. J. Fluid Mech. 600, 373–401.CrossRefGoogle Scholar
Meneghello, G., Schmid, P.J. & Huerre, P. 2015 Receptivity and sensitivity of the leading-edge boundary layer of a swept wing. J. Fluid Mech. 775, R1.CrossRefGoogle Scholar
Obrist, D. & Schmid, P. 2003 On the linear stability of swept abttachment-line boundary layer flow. Part 1. Spectrum and asymptotic behaviour. J. Fluid Mech. 493, 1–29.CrossRefGoogle Scholar
Piot, E. & Casalis, G. 2009 Absolute stability mechanism of a swept cylinder laminar boundary layer with imposed spanwise periodic conditions. Phys. Fluids 21 (6), 064103.CrossRefGoogle Scholar
Reed, H. & Saric, W. 1989 Stability of three-dimensional boundary layers. Annu. Rev. Fluid Mech. 21 (1), 235–284.CrossRefGoogle Scholar
Reed, H., Saric, W. & Arnal, D. 1996 Linear stability theory applied to boundary layers. Annu. Rev. Fluid Mech. 28 (1), 389–428.CrossRefGoogle Scholar
Saric, W., Reed, H. & White, E. 2003 Stability and transition of three-dimensional boundary layers. Annu. Rev. Fluid Mech. 35, 413–440.CrossRefGoogle Scholar
Schmid, P. & Henningson, D. 2001 Transition to turbulence. In Stability and Transition in Shear Flows, Applied Mathematical Sciences, vol. 142, pp. 401–475. Springer.CrossRefGoogle Scholar
Sipp, D. & Lebedev, A. 2007 Global stability of base and mean flows: a general approach and its applications to cylinder and open cavity flows. J. Fluid Mech. 593, 333–358.Google Scholar
Taylor, M.J. & Peake, N. 1998 The long-time behaviour of incompressible swept-wing boundary layers subject to impulsive forcing. J. Fluid Mech. 355, 359–381.CrossRefGoogle Scholar
Taylor, M.J. & Peake, N. 1999 The long-time impulse response of compressible swept-wing boundary layers. J. Fluid Mech. 379, 333–350.CrossRefGoogle Scholar
Türkylmazoglu, M. & Gajjar, J.S.B. 1999 On the absolute instability of the attachment-line and swept-Hiemenz boundary. Theor. Comput. Fluid Dyn. 13 (1), 57–75.Google Scholar
Wassermann, P. & Kloker, M. 2005 Transition mechanisms in a three-dimensional boundary-layer flow with pressure-gradient changeover. J. Fluid Mech. 530, 265–293.CrossRefGoogle Scholar