Published online by Cambridge University Press: 26 April 2023
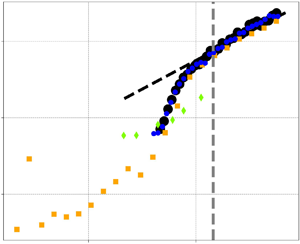
We investigate how the heat flux  $Nu$ scales with the imposed temperature gradient
$Nu$ scales with the imposed temperature gradient  $Ra$ in homogeneous Rayleigh–Bénard convection using one-, two- and three-dimensional simulations on logarithmic lattices. Logarithmic lattices are a new spectral decimation framework which enables us to span an unprecedented range of parameters (
$Ra$ in homogeneous Rayleigh–Bénard convection using one-, two- and three-dimensional simulations on logarithmic lattices. Logarithmic lattices are a new spectral decimation framework which enables us to span an unprecedented range of parameters ( $Ra$,
$Ra$,  $Re$,
$Re$,  $\Pr$) and test existing theories using little computational power. We first show that known diverging solutions can be suppressed with a large-scale friction. In the turbulent regime, for
$\Pr$) and test existing theories using little computational power. We first show that known diverging solutions can be suppressed with a large-scale friction. In the turbulent regime, for  $\Pr \approx 1$, the heat flux becomes independent of viscous processes (‘asymptotic ultimate regime’,
$\Pr \approx 1$, the heat flux becomes independent of viscous processes (‘asymptotic ultimate regime’,  $Nu\sim Ra ^{1/2}$ with no logarithmic correction). We recover scalings coherent with the theory developed by Grossmann and Lohse, for all situations where the large-scale frictions keep a constant magnitude with respect to viscous and diffusive dissipation. We also identify another turbulent friction-dominated regime at
$Nu\sim Ra ^{1/2}$ with no logarithmic correction). We recover scalings coherent with the theory developed by Grossmann and Lohse, for all situations where the large-scale frictions keep a constant magnitude with respect to viscous and diffusive dissipation. We also identify another turbulent friction-dominated regime at  $\Pr \ll 1$, where deviations from the Grossmann and Lohse prediction are observed. These two friction-dominated regimes may be relevant in some geophysical or astrophysical situations, where large-scale friction arises due to rotation, stratification or magnetic field.
$\Pr \ll 1$, where deviations from the Grossmann and Lohse prediction are observed. These two friction-dominated regimes may be relevant in some geophysical or astrophysical situations, where large-scale friction arises due to rotation, stratification or magnetic field.