Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-17T13:18:09.912Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic stability and transient growth in pulsatile Poiseuille flow through a compliant channel

Published online by Cambridge University Press:  05 May 2017

Konstantinos Tsigklifis Open the ORCID record for Konstantinos Tsigklifis [Opens in a new window]  and
Anthony D. Lucey
Konstantinos Tsigklifis*
Affiliation:
Fluid Dynamics Research Group, Department of Mechanical Engineering, Curtin University, Western Australia 6845, Australia
Anthony D. Lucey
Affiliation:
Fluid Dynamics Research Group, Department of Mechanical Engineering, Curtin University, Western Australia 6845, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The time-asymptotic linear stability of pulsatile flow in a channel with compliant walls is studied together with the evaluation of modal transient growth within the pulsation period of the basic flow as well as non-modal transient growth. Both one (vertical-displacement) and two (vertical and axial) degrees-of-freedom compliant-wall models are implemented. Two approaches are developed to study the dynamics of the coupled fluid–structure system, the first being a Floquet analysis in which disturbances are decomposed into a product of exponential growth and a sum of harmonics, while the second is a time-stepping technique for the evolution of the fundamental solution (monodromy) matrix. A parametric study of stability in the non-dimensional parameter space, principally defined by Reynolds number (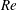$Re$), Womersley number (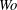$Wo$) and amplitude of the applied pressure modulation (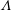$\unicode[STIX]{x1D6EC}$), is then conducted for compliant walls of fixed geometric and material properties. The flow through a rigid channel is shown to be destabilized by pulsation for low 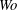$Wo$, stabilized due to Stokes-layer effects at intermediate 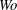$Wo$, while the critical 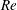$Re$ approaches the steady Poiseuille-flow result at high 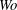$Wo$, and that these effects are made more pronounced by increasing 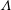$\unicode[STIX]{x1D6EC}$. Wall flexibility is shown to be stabilizing throughout the 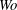$Wo$ range but, for the relatively stiff wall used, is more effective at high 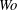$Wo$. Axial displacements are shown to have negligible effect on the results based upon only vertical deformation of the compliant wall. The effect of structural damping in the compliant-wall dynamics is destabilizing, thereby suggesting that the dominant inflectional (Rayleigh) instability is of the Class A (negative-energy) type. It is shown that very high levels of modal transient growth can occur at low 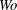$Wo$, and this mechanism could therefore be more important than asymptotic amplification in causing transition to turbulent flow for two-dimensional disturbances. Wall flexibility is shown to ameliorate mildly this phenomenon. As 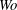$Wo$ is increased, modal transient growth becomes progressively less important and the non-modal mechanism can cause similar levels of transient growth. We also show that oblique waves having non-zero transverse wavenumbers are stable to higher values of critical 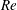$Re$ than their two-dimensional counterparts. Finally, we identify an additional instability branch at high 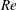$Re$ that corresponds to wall-based travelling-wave flutter. We show that this is stabilized by the inclusion of structural damping, thereby confirming that it is of the Class B (positive-energy) instability type.

JFM classification

Instability: Instability Instability: Transition to turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 820 , 10 June 2017 , pp. 370 - 399
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alexander, R. W. 1995 Hypertension and the pathogenesis of atherosclerosis. Oxidative stress and the mediation of arterial inflammatory response: a new perspective. Hypertension 25, 155–161.Google Scholar
Armentano, R. L., Barra, J. G., Santana, D. B., Pessana, F. M., Graf, S., Craiem, D., Brandani, L. M., Baglivo, H. P. & Sanchez, R. A. 2006 Smart damping modulation of carotid wall energetics in human hypertension: effects of angiotensin-converting enzyme inhibition. Hypertension 47, 384–390.CrossRefGoogle ScholarPubMed
Benjamin, T. B. 1960 Effects of a flexible boundary on hydrodynamic stability. J. Fluid Mech. 9, 513–532.CrossRefGoogle Scholar
Benjamin, T. B. 1963 The three-fold classification of unstable disturbances in flexible surfaces bounding inviscid flows. J. Fluid Mech. 16, 436–450.Google Scholar
Burke, M. A., Lucey, A. D., Howell, R. M. & Elliott, N. S. J. 2014 Stability of a flexible insert in one wall of an inviscid channel flow. J. Fluids Struct. 48, 435–450.Google Scholar
Canuto, C., Hussaini, M. Y., Quarteroni, A. & Zang, T. A. 1988 Methods in Fluid Dynamics. Springer.Google Scholar
Carpenter, P. W. & Gajjar, J. S. B. 1990 A general theory for two and three-dimensional wall-mode instabilities in boundary layers over isotropic and anisotropic compliant walls. J. Theoret. Comput. Fluid Dyn. 1, 349–378.Google Scholar
Carpenter, P. W. & Morris, P. J. 1990 The effects of anisotropic wall compliance on boundary-layer stability and transition. J. Fluid Mech. 218, 171–223.Google Scholar
Cooper, A. J. & Carpenter, P. W. 1997 The stability of rotating-disc boundary-layer flow over a compliant wall. Part 1. Type I and instabilities. J. Fluid Mech. 350, 231–259.CrossRefGoogle Scholar
Cunningham, K. S. & Gotlieb, A. I. 2005 The role of shear stress in the pathogenesis of atherosclerosis. Laboratory Investigation 85, 9–23.CrossRefGoogle ScholarPubMed
Davies, C. 2003 Convective and absolute instabilities of flow over compliant walls. In Flow Past Highly Compliant Boundaries and in Collapsible Tubes, vol. 72, pp. 69–93. Springer.Google Scholar
Davies, C. & Carpenter, P. W. 1997a Instabilities in a plane channel flow between compliant walls. J. Fluid Mech. 352, 205–243.Google Scholar
Davies, C. & Carpenter, P. W. 1997b Numerical simulation of the evolution of Tollmien–Schlichting waves over finite compliant panels. J. Fluid Mech. 335, 361–392.CrossRefGoogle Scholar
Davis, S. H. 1976 The stability of time-periodic flows. Annu. Rev. Fluid Mech. 8, 57–74.Google Scholar
Einav, S. & Sokolov, M. 1993 An experimental study of pulsatile pipe flow in the transition range. J. Biomech. Engng 115, 404–411.Google Scholar
Gaster, M. 1988 Is the dolphin a red herring? Turbulence Management and Relaminarisation. pp. 285–304. Springer.CrossRefGoogle Scholar
Hall, P. 1975 The stability of Poiseuille flow modulated at high frequencies. Proc. R. Soc. Lond. A 344, 453–464.Google Scholar
Hœpffner, J., Bottaro, A. & Favier, J. 2010 Mechanisms of non-modal energy amplification in channel flow between compliant walls. J. Fluid Mech. 642, 489–507.Google Scholar
Iooss, G. & Joseph, D. D. 1990 Elementary Stability and Bifurcation Theory. Springer.Google Scholar
Kapor, J. S. & Lucey, A. D. 2012 Flow-induced vibrations of a flexible panel in a boundary-layer flow. In The 10th International Conference on Flow Induced Vibration, 2–6 July 2012 (ed. Meskell, C. & Bennet, G.), pp. 647–654. Ex Ordo.Google Scholar
Kapor, J. S., Lucey, A. D. & Pitman, M. W. 2009 Boundary-layer hydrodynamics using mesh-free modelling. In The 18th World IMACS Congress and MODSIM09 International Congress on Modelling and Simulation, 13 July 2009 (ed. Anderssen, R. S., Braddock, R. D. & Newham, L. T. H.), pp. 1725–1731. Modelling and Simulation Society of Australia and New Zealand and International Association for Mathematics and Computers in Simulation.Google Scholar
Landahl, M. T. 1962 On the stability of a laminar incompressible boundary layer over a flexible surface. J. Fluid Mech. 13, 609–632.Google Scholar
Lucey, A. D. & Carpenter, P. W. 1992 A numerical simulation of the interaction of a compliant wall and inviscid flow. J. Fluid Mech. 234, 121–146.Google Scholar
Lucey, A. D. & Carpenter, P. W. 1993 The hydroelastic stability of three-dimensional disturbances of a finite compliant wall. J. Sound Vib. 165 (3), 527–552.Google Scholar
Lucey, A. D. & Carpenter, P. W. 1995 Boundary layer instability over compliant walls: comparison between theory and experiment. Phys. Fluids 7, 2355–2363.Google Scholar
Malik, S. V. & Hooper, A. P. 2007 Three-dimensional disturbances in channel flows. Phys. Fluids 19, 052102.Google Scholar
Mao, X., Sherwin, S. J. & Blackburn, H. M. 2009 Transient growth and bypass transition in stenotic flow with a physiological waveform. Theor. Comput. Fluid Dyn. 25, 31–42.Google Scholar
Meyer, C. D. 2000 Matrix Analysis and Applied Linear Algebra. SIAM.CrossRefGoogle Scholar
Nerem, R. M., Seed, W. A. & Wood, N. B. 1972 An experimental study of the velocity distribution and transition to turbulence in the aorta. J. Fluid Mech. 52, 137–160.Google Scholar
Pitman, M. W. & Lucey, A. D. 2009 On the direct determination of the eigenmodes of finite flow-structure systems. Proc. R. Soc. Lond. A 465, 257–281.Google Scholar
Reddy, S. C., Schmid, P. J. & Henningson, D. S. 1993 Pseudospectra of the Orr–Sommerfeld operator. SIAM J. Appl. Maths 53 (1), 15–47.CrossRefGoogle Scholar
Schmid, P. J. 2007 Nonmodal stability theory. Annu. Rev. Fluid Mech. 39, 129–162.CrossRefGoogle Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows. Springer.CrossRefGoogle Scholar
Schmid, P. J. & Kytomaa, H. K. 1994 Transient and asymptotic stability of granular shear flow. J. Fluid Mech. 264, 255–275.Google Scholar
Seydel, R. 1988 From Equilibrium to Chaos. Practical Bifurcation and Stability Analysis. Elsevier.Google Scholar
Shankar, V. & Kumaran, V. 2002 Stability of wall modes in fluid flow past a flexible surface. Phys. Fluids 14, 2324–2338.Google Scholar
Singer, B. A., Ferziger, J. H. & Reed, H. L. 1989 Numerical simulations of transition in oscillatory plane channel flow. J. Fluid Mech. 208, 45–66.CrossRefGoogle Scholar
Straatman, A. G., Khayat, R. E., Haj-Qasem, E. & Steinman, D. A. 2002 On the hydrodynamic stability of pulsatile flow in a plane channel. Phys. Fluids 14, 1938–1944.Google Scholar
Thaokar, R. M. & Kumaran, V. 2004 Stability of oscillatory flows past compliant surfaces. Eur. Phys. J. B 41, 135–145.Google Scholar
Thomas, C., Bassom, A. P., Blennerhassett, P. J. & Davies, C. 2011 The linear stability of oscillatory Poiseuille flow in channels and pipes. Proc. R. Soc. Lond. A 467, 2643–2662.Google Scholar
Timoshenko, S. & Woinowsky-Krieger, S. 1959 Theory of Plates and Shells. McGraw-Hill.Google Scholar
Tsigklifis, K. & Lucey, A. D. 2015 Global instabilities and transient growth in Blasius boundary-layer flow over a compliant panel. Sadhana 40, 945–960.Google Scholar
Tsiglifis, K. & Pelekasis, N. A. 2011 Parametric stability and dynamic buckling of an encapsulated microbubble subject to acoustic disturbances. Phys. Fluids 23, 012102.CrossRefGoogle Scholar
Von Kerczek, C. H. 1982 The instability of oscillatory plane Poiseuille flow. J. Fluid Mech. 116, 91–114.CrossRefGoogle Scholar
Von Kerczek, C. & Davis, S. H. 1974 Linear stability theory of oscillatory Stokes layers. J. Fluid Mech. 62, 753–773.Google Scholar
Yeo, K. S. 1992 The three-dimensional stability of boundary-layer flow over compliant walls. J. Fluid Mech. 238, 537–577.Google Scholar