Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T09:32:49.290Z Has data issue: false hasContentIssue false
  • English
  • Français

Aspect ratio-dependent hysteresis response of a heavy inverted flag

Published online by Cambridge University Press:  13 May 2022

Oluwafemi Ojo Open the ORCID record for Oluwafemi Ojo [Opens in a new window] ,
Yu-Cheng Wang ,
Alper Erturk Open the ORCID record for Alper Erturk [Opens in a new window]  and
Kourosh Shoele Open the ORCID record for Kourosh Shoele [Opens in a new window]
Oluwafemi Ojo
Affiliation:
Department of Mechanical Engineering, Joint College of Engineering, Florida A&M University-Florida State University, Tallahassee, FL 32310, USA
Yu-Cheng Wang
Affiliation:
G.W. Woodruff School of Mechanical Engineering, Georgia Institute of Technology, Atlanta, GA 30332, USA
Alper Erturk
Affiliation:
G.W. Woodruff School of Mechanical Engineering, Georgia Institute of Technology, Atlanta, GA 30332, USA
Kourosh Shoele*
Affiliation:
Department of Mechanical Engineering, Joint College of Engineering, Florida A&M University-Florida State University, Tallahassee, FL 32310, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

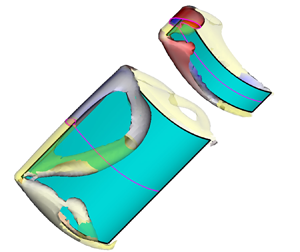
The bistable fluttering response of heavy inverted flags with different aspect ratios ($AR$) is investigated to determine how the vortical structures affect the intermittent vibration response of the flag. A heavy inverted flag in a uniform flow may exhibit several response modes; amongst them are three major modes that occur over an extended velocity range: stationary, large-scale periodic oscillation and one-sided deflected modes. Significant hysteretic bistability is observed at the transition between these modes for all $AR$, which is notably different from the conventional flag vibration with a fixed leading edge and free trailing edge where no hysteresis is observed at the lower $AR$ limit ($AR<1$). The difference is associated with the distinct roles of vortices around the flag. Experiments with flags made of spring steel are conducted in a wind tunnel, where the flow speed is steadily increased and later decreased to obtain different oscillatory modes of the heavy inverted flags. The experimental results are used to validate the numerical model of the same problem. It is found that different critical velocities exist for increasing and decreasing flow velocities, and there is a sustained hysteresis for all $AR$ controlled by the initiation threshold and growth of the leading-edge and side-edge vortices. The effect of the vortices in the bistable oscillation regime is quantified by formulating a modal force partitioning approach. It is shown that $AR$ can significantly alter the static and dynamic vortex interaction with the flexible plate, thereby changing the flag's hysteresis behaviour and bistable response.

JFM classification

Aerodynamics: Flow-structure interactions Nonlinear Dynamical Systems: Bifurcation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 942 , 10 July 2022 , A4
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bollay, W. 1939 A non-linear wing theory and its application to rectangular wings of small aspect ratio. Z. Angew. Math. Mech. 19 (1), 21–35.CrossRefGoogle Scholar
Eldredge, J.D. & Jones, A.R. 2019 Leading-edge vortices: mechanics and modeling. Annu. Rev. Fluid Mech. 51, 75–104.CrossRefGoogle Scholar
Eloy, C., Kofman, N. & Schouveiler, L. 2012 The origin of hysteresis in the flag instability. J. Fluid Mech. 691, 583–593.CrossRefGoogle Scholar
Goldstein, D, Handler, R. & Sirovich, L. 1993 Modeling a no-slip flow boundary with an external force field. J. Comput. Phys. 105 (2), 354–366.CrossRefGoogle Scholar
Goza, A., Colonius, T. & Sader, J.E. 2018 Global modes and nonlinear analysis of inverted-flag flapping. J. Fluid Mech. 857, 312–344.CrossRefGoogle Scholar
Gurugubelli, P.S. & Jaiman, R.K. 2019 Large amplitude flapping of an inverted elastic foil in uniform flow with spanwise periodicity. J. Fluids Struct. 90, 139–163.CrossRefGoogle Scholar
Kim, D., Cossé, J., Huertas-Cerdeira, C. & Gharib, M. 2013 Flapping dynamics of an inverted flag. J. Fluid Mech. 736, R1.CrossRefGoogle Scholar
Krishnasamy, G., Rizzo, F.J. & Liu, Y. 1994 Boundary integral equations for thin bodies. Intl J. Numer. Meth. Engng 37 (1), 107–121.CrossRefGoogle Scholar
Martin, P.A. & Risso, F.J. 1993 Boundary integral equations for bodies of small, but finite, thickness. In Proceedings of Eighth Int'l Workshop on Water Waves and Floating Bodies, pp. 91–94.Google Scholar
Menon, K. & Mittal, R. 2021 a On the initiation and sustenance of flow-induced vibration of cylinders: insights from force partitioning. J. Fluid Mech. 907, A37.CrossRefGoogle Scholar
Menon, K. & Mittal, R. 2021 b Quantitative analysis of the kinematics and induced aerodynamic loading of individual vortices in vortex-dominated flows: a computation and data-driven approach. J. Comput. Phys. 443, 110515.CrossRefGoogle Scholar
Mittal, R., Dong, H., Bozkurttas, M., Najjar, F.M., Vargas, A. & Von Loebbecke, A. 2008 A versatile sharp interface immersed boundary method for incompressible flows with complex boundaries. J. Comput. Phys. 227 (10), 4825–4852.CrossRefGoogle ScholarPubMed
Ojo, O., Shoele, K., Erturk, A., Wang, Y.-C. & Kohtanen, E. 2021 Numerical and experimental investigations of energy harvesting from piezoelectric inverted flags. In AIAA Scitech 2021 Forum, p. 1323.Google Scholar
Ojo, O., Tan, D., Wang, Y.-C., Shoele, K. & Erturk, A. 2019 Aspect ratio effects in wind energy harvesting using piezoelectric inverted flags. In Active and Passive Smart Structures and Integrated Systems XIII, vol. 10967, p. 109670Q. International Society for Optics and Photonics.CrossRefGoogle Scholar
Orrego, S., Shoele, K., Ruas, A., Doran, K., Caggiano, B., Mittal, R. & Kang, S.H. 2017 Harvesting ambient wind energy with an inverted piezoelectric flag. Appl. Energy 194, 212–222.CrossRefGoogle Scholar
Park, J.W., Ryu, J. & Sung, H.J. 2019 Effects of the shape of an inverted flag on its flapping dynamics. Phys. Fluids 31 (2), 021904.Google Scholar
Peskin, C.S. 2002 The immersed boundary method. Acta Numerica 11, 479–517.CrossRefGoogle Scholar
Polhamus, E.C. 1966 A concept of the vortex lift of sharp-edge delta wings based on a leading-edge-suction analogy. NASA TND–3767.Google Scholar
Quartapelle, L. & Napolitano, M. 1983 Force and moment in incompressible flows. AIAA J. 21 (6), 911–913.CrossRefGoogle Scholar
Sader, J.E, Cossé, J., Kim, D., Fan, B. & Gharib, M. 2016 a Large-amplitude flapping of an inverted flag in a uniform steady flow–a vortex-induced vibration. J. Fluid Mech. 793, 524–555.CrossRefGoogle Scholar
Sader, J.E, Huertas-Cerdeira, C. & Gharib, M. 2016 b Stability of slender inverted flags and rods in uniform steady flow. J. Fluid Mech. 809, 873–894.CrossRefGoogle Scholar
Shelley, M.J. & Zhang, J. 2011 Flapping and bending bodies interacting with fluid flows. Annu. Rev. Fluid Mech. 43, 449–465.CrossRefGoogle Scholar
Shoele, K. & Mittal, R. 2016 Energy harvesting by flow-induced flutter in a simple model of an inverted piezoelectric flag. J. Fluid Mech. 790, 582–606.CrossRefGoogle Scholar
Taira, K. & Colonius, T.I.M. 2009 Three-dimensional flows around low-aspect-ratio flat-plate wings at low Reynolds numbers. J. Fluid Mech. 623, 187–207.CrossRefGoogle Scholar
Tang, C., Liu, N.-S. & Lu, X.-Y. 2015 Dynamics of an inverted flexible plate in a uniform flow. Phys. Fluids 27 (7), 073601.CrossRefGoogle Scholar
Tavallaeinejad, M., Legrand, M. & Paidoussis, M.P. 2020 a Nonlinear dynamics of slender inverted flags in uniform steady flows. J. Sound Vib. 467, 115048.CrossRefGoogle Scholar
Tavallaeinejad, M., Païdoussis, M.P, Legrand, M. & Kheiri, M. 2020 b Instability and the post-critical behaviour of two-dimensional inverted flags in axial flow. J. Fluid Mech. 890, A14.CrossRefGoogle Scholar
Tavallaeinejad, M., Païdoussis, M.P, Salinas, M.F., Legrand, M., Kheiri, M. & Botez, R.M. 2020 c Flapping of heavy inverted flags: a fluid-elastic instability. J. Fluid Mech. 904, R5.CrossRefGoogle Scholar
Tavallaeinejad, M., Salinas, M.F., Païdoussis, M.P., Legrand, M., Kheiri, M. & Botez, R.M. 2021 Dynamics of inverted flags: experiments and comparison with theory. J. Fluids Struct. 101, 103199.CrossRefGoogle Scholar
Vahab, M., Sussman, M. & Shoele, K. 2021 Fluid-structure interaction of thin flexible bodies in multi-material multi-phase systems. J. Comput. Phys. 429, 110008.CrossRefGoogle Scholar
Yu, Z. & Eloy, C. 2018 Extension of lighthill's slender-body theory to moderate aspect ratios. J. Fluids Struct. 76, 84–94.CrossRefGoogle Scholar
Yu, Y., Liu, Y. & Amandolese, X. 2019 A review on fluid-induced flag vibrations. Appl. Mech. Rev. 71 (1), 010801.CrossRefGoogle Scholar