Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-26T23:36:07.191Z Has data issue: false hasContentIssue false
  • English
  • Français

Aspect ratio dependence of heat transport by turbulent Rayleigh–Bénard convection in rectangular cells

Published online by Cambridge University Press:  28 August 2012

Quan Zhou ,
Bo-Fang Liu ,
Chun-Mei Li  and
Bao-Chang Zhong
Quan Zhou*
Affiliation:
Shanghai Institute of Applied Mathematics and Mechanics, and Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai University, Shanghai 200072, China
Bo-Fang Liu
Affiliation:
Shanghai Institute of Applied Mathematics and Mechanics, and Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai University, Shanghai 200072, China
Chun-Mei Li
Affiliation:
Shanghai Institute of Applied Mathematics and Mechanics, and Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai University, Shanghai 200072, China
Bao-Chang Zhong
Affiliation:
Shanghai Institute of Applied Mathematics and Mechanics, and Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai University, Shanghai 200072, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

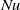We report high-precision measurements of the Nusselt number as a function of the Rayleigh number 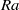in water-filled rectangular Rayleigh–Bénard convection cells. The horizontal length 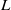and width 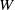of the cells are 50.0 and 15.0 cm, respectively, and the heights 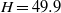, 25.0, 12.5, 6.9, 3.5, and 2.4 cm, corresponding to the aspect ratios 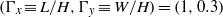, , 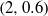, , 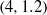, 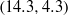and 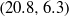. The measurements were carried out over the Rayleigh number range 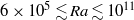and the Prandtl number range 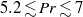. Our results show that for rectangular geometry turbulent heat transport is independent of the cells’ aspect ratios and hence is insensitive to the nature and structures of the large-scale mean flows of the system. This is slightly different from the observations in cylindrical cells where 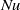is found to be in general a decreasing function of 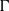, at least for 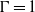and larger. Such a difference is probably a manifestation of the finite plate conductivity effect. Corrections for the influence of the finite conductivity of the top and bottom plates are made to obtain the estimates of 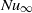for plates with perfect conductivity. The local scaling exponents 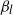of 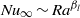are calculated and found to increase from 0.243 at 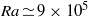to 0.327 at .

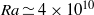JFM classification

Turbulent Flows: Turbulent convection Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 710 , 10 November 2012 , pp. 260 - 276
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Ahlers, G., Brown, B., Araujo, F. F., Funfschilling, D., Grossmann, S. & Lohse, D. 2006 Non-Oberbeck–Boussinesq effects in strongly turbulent Rayleigh–Bénard convection. J. Fluid Mech. 569, 409–445.CrossRefGoogle Scholar
2. Ahlers, G., Funfschilling, D. & Bodenschatz, E. 2009a Transitions in heat transport by turbulent convection at Rayleigh numbers up to . New J. Phys. 11, 123001.CrossRefGoogle Scholar
3. Ahlers, G., Grossmann, S. & Lohse, D. 2009b Heat transfer and large-scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.CrossRefGoogle Scholar
4. Ahlers, G. & Xu, X.-C. 2001 Prandtl-number dependence of heat transport in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 86, 3320–3323.CrossRefGoogle ScholarPubMed
5. Bailon-Cuba, J., Emran, M. S. & Schumacher, J. 2010 Aspect ratio dependence of heat transfer and large-scale flow in turbulent convection. J. Fluid Mech. 655, 152–173.CrossRefGoogle Scholar
6. Brown, E., Nikolaenko, A., Funfschilling, D. & Ahlers, G. 2005 Heat transport in turbulent Rayleigh–Bénard convection: effect of finite top- and bottom-plate conductivities. Phys. Fluids 17, 075108.CrossRefGoogle Scholar
7. Castaing, B., Gunaratne, G., Heslot, F., Kadanoff, L., Libchaber, A., Thomae, S., Wu, X.-Z., Zaleski, S. & Zanetti, G. 1989 Scaling of hard thermal turbulence in Rayleigh–Bénard convection. J. Fluid Mech. 204, 1–30.CrossRefGoogle Scholar
8. Chavanne, X., Chilla, F., Castaing, B., Hebral, B., Chabaud, B. & Chaussy, J. 1997 Observation of the ultimate regime in Rayleigh–Bénard convection. Phys. Rev. Lett. 79, 3648–3651.CrossRefGoogle Scholar
9. Chavanne, X., Chilla, F., Chabaud, B., Castaing, B. & Hebral, B. 2001 Turbulent Rayleigh–Bénard convection in gaseous and liquid He. Phys. Fluids 13, 1300–1320.CrossRefGoogle Scholar
10. Cheung, Y. H. 2004 Aspect-ratio dependence of the Nusselt number and boundary layer properties in Rayleigh–Bénard turbulent convection. MPhil thesis, The Chinese University of Hong Kong.Google Scholar
11. Ching, E. S. C. & Tam, W. S. 2006 Aspect-ratio dependence of heat transport by turbulent Rayleigh–Bénard convection. J. Turbul. 7, 72.CrossRefGoogle Scholar
12. Du, Y.-B. & Tong, P. 2000 Turbulent thermal convection in a cell with ordered rough boundaries. J. Fluid Mech. 407, 57–84.CrossRefGoogle Scholar
13. Dubrulle, B. 2001 Logarithmic corrections to scaling in turbulent thermal convection. Eur. Phys. J. B 21, 295–304.Google Scholar
14. Dubrulle, B. 2002 Scaling in large Prandtl number turbulent thermal convection. Eur. Phys. J. B 28, 361–367.CrossRefGoogle Scholar
15. Fleischer, A. S. & Goldstein, R. J. 2002 High-Rayleigh-number convection of pressurized gases in a horizontal enclosure. J. Fluid Mech. 469, 1–12.CrossRefGoogle Scholar
16. Funfschilling, D., Bodenschatz, E. & Ahlers, G. 2009 Search for the ‘ultimate state’ in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 103, 014503.CrossRefGoogle Scholar
17. Funfschilling, D., Brown, E., Nikolaenko, A. & Ahlers, G. 2005 Heat transport by turbulent Rayleigh–Bénard convection in cylindrical samples with aspect ratio one and larger. J. Fluid Mech. 536, 145–154.CrossRefGoogle Scholar
18. Gasteuil, Y., Shew, W. L., Gibert, M., Chilla, F., Castaing, B. & Pinton, J.-F. 2007 Lagrangian temperature, velocity, and local heat flux measurement in Rayleigh–Bénard convection. Phys. Rev. Lett. 99, 234302.CrossRefGoogle ScholarPubMed
19. Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.CrossRefGoogle Scholar
20. Grossmann, S. & Lohse, D. 2001 Thermal convection for large Prandtl numbers. Phys. Rev. Lett. 86, 3316–3319.CrossRefGoogle ScholarPubMed
21. Grossmann, S. & Lohse, D. 2003 On geometry effects in Rayleigh–Bénard convection. J. Fluid Mech. 486, 105–114.CrossRefGoogle Scholar
22. Grossmann, S. & Lohse, D. 2004 Fluctuations in turbulent Rayleigh–Bénard convection: the role of plumes. Phys. Fluids 16, 4462.CrossRefGoogle Scholar
23. Grossmann, S. & Lohse, D. 2011 Multiple scaling in the ultimate regime of thermal convection. Phys. Fluids 23, 045108.CrossRefGoogle Scholar
24. He, X.-Z., Funfschilling, D., Nobach, H., Bodenschatz, E. & Ahlers, G. 2012 Transition to the ultimate state of turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 108, 024502.CrossRefGoogle Scholar
25. Johnston, H. & Doering, C. R. 2009 Comparison of turbulent thermal convection between conditions of constant temperature and constant flux. Phys. Rev. Lett. 102, 064501.CrossRefGoogle ScholarPubMed
26. Kerr, R. M. 1996 Rayleigh number scaling in numerical convection. J. Fluid Mech. 310, 139–179.CrossRefGoogle Scholar
27. Kerr, R. M. & Herring, J. 2000 Prandtl number dependence of Nusselt number in direct numerical simulations. J. Fluid Mech. 491, 325–344.CrossRefGoogle Scholar
28. Lohse, D. & Xia, K.-Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42, 335–364.CrossRefGoogle Scholar
29. Maystrenko, A., Resagk, C. & Thess, A. 2007 Structure of the thermal boundary layer for turbulent Rayleigh–Bénard convection of air in a long rectangular enclosure. Phys. Rev. E 75, 066303.CrossRefGoogle Scholar
30. Niemela, J. J., Skrbek, L., Sreenivasan, K. R. & Donnelly, R. J. 2000 Turbulent convection at very high Rayleigh numbers. Nature 404, 837–840.CrossRefGoogle ScholarPubMed
31. Niemela, J. J. & Sreenivasan, K. R. 2003 Confined turbulent convection. J. Fluid Mech. 481, 355–384.CrossRefGoogle Scholar
32. Niemela, J. J. & Sreenivasan, K. R. 2006 Turbulent convection at high Rayleigh numbers and aspect ratio 4. J. Fluid Mech. 557, 411–422.CrossRefGoogle Scholar
33. Nikolaenko, A., Brown, E., Funfschilling, D. & Ahlers, G. 2005 Heat transport by turbulent Rayleigh–Bénard convection in cylindrical cells with aspect ratio one and less. J. Fluid Mech. 523, 251–260.CrossRefGoogle Scholar
34. van der Poel, E. P., Stevens, R. J. A. M. & Lohse, D. 2011 Connecting flow structures and heat flux in turbulent Rayleigh–Bénard convection. Phys. Rev. E 84, 045303(R).CrossRefGoogle ScholarPubMed
35. Press, W. H., Teukolsky, S., Vetterling, W. & Flannery, B. 1986 Numerical Recipes. Cambridge University Press.Google Scholar
36. du Puits, R., Resagk, C. & Thess, A. 2007 Breakdown of wind in turbulent thermal convection. Phys. Rev. E 75, 016302.CrossRefGoogle ScholarPubMed
37. Roche, P.-E., Castaing, B., Chabaud, B. & Hébral, B. 2002 Prandtl and Rayleigh numbers dependences in Rayleigh–Bénard convection. Europhys. Lett. 58, 693–698.CrossRefGoogle Scholar
38. Roche, P.-E., Gauthier, F., Chabaud, B. & Hébral, B. 2005 Ultimate regime of convection: robustness to poor thermal reservoirs. Phys. Fluids 17, 115107.CrossRefGoogle Scholar
39. Roche, P.-E., Gauthier, F., Kaiser, R. & Salort, J. 2010 On the triggering of the ultimate regime of convection. New J. Phys. 12, 085014.CrossRefGoogle Scholar
40. Shishkina, O. & Wagner, C. 2007 Local heat fluxes in turbulent Rayleigh–Bénard convection. Phys. Fluids 19, 085107.CrossRefGoogle Scholar
41. Shraiman, B. I. & Siggia, E. D. 1990 Heat transport in high-Rayleigh-number convection. Phys. Rev. A 42, 3650–3653.CrossRefGoogle ScholarPubMed
42. Silano, G., Sreenivasan, K. R. & Verzicco, R. 2010 Numerical simulations of Rayleigh–Bénard convection for Prandtl numbers between and and Rayleigh numbers between and . J. Fluid Mech. 662, 409–446.CrossRefGoogle Scholar
43. Song, H. & Tong, P. 2010 Scaling laws in turbulent Rayleigh–Bénard convection under different geometry. Europhys. Lett. 90, 44001.CrossRefGoogle Scholar
44. Stevens, R. J. A. M., Lohse, D. & Verzicco, R. 2011 Prandtl and Rayleigh number dependence of heat transport in high Rayleigh number thermal convection. J. Fluid Mech. 688, 31–43.CrossRefGoogle Scholar
45. Stevens, R. J. A. M., Verzicco, R. & Lohse, D. 2010 Radial boundary layer structure and Nusselt number in Rayleigh–Bénard convection. J. Fluid Mech. 643, 495–507.CrossRefGoogle Scholar
46. Sugiyama, K., Ni, R., Stevens, R. J. A. M., Chan, T.-S., Zhou, S.-Q., Xi, H.-D., Sun, C., Grossmann, S., Xia, K.-Q. & Lohse, D. 2010 Flow reversals in thermally driven turbulence. Phys. Rev. Lett. 105, 034503.CrossRefGoogle ScholarPubMed
47. Sun, C., Ren, L.-Y., Song, H. & Xia, K.-Q. 2005a Heat transport by turbulent Rayleigh–Bénard convection in 1 m diameter cylindrical cells of widely varying aspect ratio. J. Fluid Mech. 542, 165–174.CrossRefGoogle Scholar
48. Sun, C., Xi, H.-D. & Xia, K.-Q. 2005b Azimuthal symmetry, flow dynamics, and heat transport in turbulent thermal convection in a cylinder with an aspect ratio of 0.5. Phys. Rev. Lett. 95, 074502.CrossRefGoogle Scholar
49. Verzicco, R. 2004 Effects of nonperfect thermal sources in turbulent thermal convection. Phys. Fluids 16, 1965–1979.CrossRefGoogle Scholar
50. Verzicco, R. & Camussi, R. 2003 Numerical experiments on strongly turbulent thermal convection in a slender cylindrical cell. J. Fluid Mech. 477, 19–49.CrossRefGoogle Scholar
51. Wagner, S., Shishkina, O. & Wagner, C. 2012 Boundary layers and wind in cylindrical Rayleigh–Bénard cells. J. Fluid Mech. 697, 336–366.CrossRefGoogle Scholar
52. Weiss, S., Stevens, R. J. A. M., Zhong, J.-Q., Clercx, H. J. H., Lohse, D. & Ahlers, G. 2010 Finite-size effects lead to supercritical bifurcations in turbulent rotating Rayleigh–Bénard convection. Phys. Rev. Lett. 105, 224501.CrossRefGoogle ScholarPubMed
53. Xi, H.-D. & Xia, K.-Q. 2008 Azimuthal motion, reorientation, cessation, and reversal of the large-scale circulation in turbulent thermal convection: a comparative study in aspect ratio one and one-half geometries. Phys. Rev. E 78, 036326.CrossRefGoogle ScholarPubMed
54. Xia, K.-Q., Lam, S. & Zhou, S.-Q. 2002 Heat-flux measurement in high-Prandtl-number turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 88, 064501.CrossRefGoogle ScholarPubMed
55. Xia, K.-Q., Sun, C. & Cheung, Y.-H. 2008 Large scale velocity structures in turbulent thermal convection with widely varying aspect ratio. 14th International Symposium on Applications of Laser Techniques to Fluid Mechanics.Google Scholar
56. Xia, K.-Q., Sun, C. & Zhou, S.-Q. 2003 Particle image velocimetry measurement of the velocity field in turbulent thermal convection. Phys. Rev. E 68, 066303.CrossRefGoogle ScholarPubMed
57. Xu, X.-C., Bajaj, K. M. S. & Ahlers, G. 2000 Heat transport in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 84, 4357–4360.CrossRefGoogle ScholarPubMed
58. Zhou, Q., Stevens, R. J. A. M., Sugiyama, K., Grossmann, S., Lohse, D. & Xia, K.-Q. 2010 Prandtl–Blasius temperature and velocity boundary-layer profiles in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 664, 297–312.CrossRefGoogle Scholar
59. Zhou, Q. & Xia, K.-Q. 2008 Comparative experimental study of local mixing of active and passive scalars in turbulent thermal convection. Phys. Rev. E 77, 056312.CrossRefGoogle ScholarPubMed
60. Zhou, Q. & Xia, K.-Q. 2010a Measured instantaneous viscous boundary layer in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 104, 104301.CrossRefGoogle ScholarPubMed
61. Zhou, Q. & Xia, K.-Q. 2010b The mixing evolution and geometric properties of a passive scalar field in turbulent Rayleigh–Bénard convection. New J. Phys. 12, 083029.CrossRefGoogle Scholar
62. Zhou, S.-Q., Sun, C. & Xia, K.-Q. 2007 Measured oscillations of the velocity and temperature fields in turbulent Rayleigh–Bénard convection in a rectangular cell. Phys. Rev. E 76, 036301.CrossRefGoogle Scholar