Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T04:04:24.987Z Has data issue: false hasContentIssue false
  • English
  • Français

Approximate solutions to droplet dynamics in Hele-Shaw flows

Published online by Cambridge University Press:  23 August 2018

Yoav Green Open the ORCID record for Yoav Green [Opens in a new window]
Yoav Green*
Affiliation:
Harvard T.H. Chan School of Public Health, Boston, MA 02115, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For the past decade, the interaction force between droplets flowing in a Hele-Shaw cell has been modelled as a dipole. In this work, we use the recently derived analytical solution of Sarig et al. (J. Fluid Mech., vol. 800, 2016, pp. 264–277) of a two-droplet system, which satisfies the no-flux condition at both droplet interfaces, and compare it to results of the dipole model, which does not satisfy the no-flux condition. Unfortunately, the recently derived solution is given in terms of infinite Fourier series, making any additional straightforward analysis difficult. We derive simple approximations for these Fourier series. We show that at large spacing the approximations for the interactions reduce to the expected dipole-like solution. We also provide a new lower limit for the velocity for the case of almost touching droplets. For the case of large spacing, the derivation is extended to arbitrary droplet numbers – including an infinite lattice. We present a new correction for the dispersion relation for the perturbations. We investigate the effect of the number of droplets in a lattice, 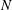$N$, on the resulting dynamics.

JFM classification

Low-Reynolds-number flows: Hele-Shaw flows Low-Reynolds-number flows: Low-Reynolds-number flows Micro-/Nano-fluid dynamics: Microfluidics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 853 , 25 October 2018 , pp. 253 - 270
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work was conducted primarily at the Faculty of Mechanical Engineering, Technion–Israel Institute of Technology, Technion City 3200003, Israel.

References

Beatus, T., Bar-Ziv, R. & Tlusty, T. 2007 Anomalous microfluidic phonons induced by the interplay of hydrodynamic screening and incompressibility. Phys. Rev. Lett. 99 (12), 124502.Google Scholar
Beatus, T., Bar-Ziv, R. H. & Tlusty, T. 2012 The physics of 2D microfluidic droplet ensembles. Phys. Rep. 516 (3), 103–145.Google Scholar
Beatus, T., Tlusty, T. & Bar-Ziv, R. 2006 Phonons in a one-dimensional microfluidic crystal. Nat. Phys. 2 (11), 743–748.Google Scholar
Beatus, T., Tlusty, T. & Bar-Ziv, R. 2009 Burgers shock waves and sound in a 2D microfluidic droplets ensemble. Phys. Rev. Lett. 103 (11), 114502.Google Scholar
Belloul, M., Engl, W., Colin, A., Panizza, P. & Ajdari, A. 2009 Competition between local collisions and collective hydrodynamic feedback controls traffic flows in microfluidic networks. Phys. Rev. Lett. 102 (19), 194502.Google Scholar
Bretherton, F. P. 1961 The motion of long bubbles in tubes. J. Fluid Mech. 10 (2), 166–188.Google Scholar
Champagne, N., Lauga, E. & Bartolo, D. 2011 Stability and non-linear response of 1D microfluidic-particle streams. Soft Matt. 7 (23), 11082–11085.Google Scholar
Champagne, N., Vasseur, R., Montourcy, A. & Bartolo, D. 2010 Traffic jams and intermittent flows in microfluidic networks. Phys. Rev. Lett. 105 (4), 044502.Google Scholar
Christopher, G. F., Noharuddin, N. N., Taylor, J. A. & Anna, S. L. 2008 Experimental observations of the squeezing-to-dripping transition in T-shaped microfluidic junctions. Phys. Rev. E 78 (3), 036317.Google Scholar
Crowdy, D. G., Surana, A. & Yick, K.-Y. 2007 The irrotational motion generated by two planar stirrers in inviscid fluid. Phys. Fluids 19 (1), 018103.Google Scholar
Currie, I. G. 1974 Fundamental Mechanics of Fluids. McGraw-Hill.Google Scholar
Desreumaux, N., Caussin, J.-B., Jeanneret, R., Lauga, E. & Bartolo, D. 2013 Hydrodynamic fluctuations in confined particle-laden fluids. Phys. Rev. Lett. 111 (11), 118301.Google Scholar
Garstecki, P., Gitlin, I., Diluzio, W., Whitesides, G. M., Kumacheva, E. & Stone, H. A. 2004 Formation of monodisperse bubbles in a microfluidic flow-focusing device. Appl. Phys. Lett. 85 (13), 2649–2651.Google Scholar
Gradshteyn, I. S. & Ryzhik, I. M. 2007 Table of Integrals, Series, and Products, 7th edn. Academic Press.Google Scholar
Green, C. C., Lustri, C. J. & McCue, S. W. 2017 The effect of surface tension on steadily translating bubbles in an unbounded Hele-Shaw cell. Proc. R. Soc. Lond. A 473 (2201), 20170050.Google Scholar
Hodges, S. R., Jensen, O. E. & Rallison, J. M. 2004 The motion of a viscous drop through a cylindrical tube. J. Fluid Mech. 501, 279–301.Google Scholar
Huerre, A., Theodoly, O., Leshansky, A. M., Valignat, M.-P., Cantat, I. & Jullien, M.-C. 2015 Droplets in microchannels: dynamical properties of the lubrication film. Phys. Rev. Lett. 115 (6), 064501.Google Scholar
Joanicot, M. & Ajdari, A. 2005 Droplet control for microfluidics. Science 309 (5736), 887–888.Google Scholar
Kittel, C. 1986 Introduction to Solid State Physics. Wiley.Google Scholar
Kopf-Sill, A. R. & Homsy, G. M. 1987 Narrow fingers in a Hele-Shaw cell. Phys. Fluids 30 (9), 2607–2609.Google Scholar
Landau, L. D. & Lifshitz, E. M. 1959 Fluid Mechanics. Pergamon.Google Scholar
Lewin, L. 1991 Structural Properties of Polylogarithms. American Mathematical Society.Google Scholar
Link, D. R., Anna, S. L., Weitz, D. A. & Stone, H. A. 2004 Geometrically mediated breakup of drops in microfluidic devices. Phys. Rev. Lett. 92 (5), 054503.Google Scholar
Liu, B., Goree, J. & Feng, Y. 2012 Waves and instability in a one-dimensional microfluidic array. Physical Review E 86 (4), 046309.Google Scholar
Maxworthy, T. 1986 Bubble formation, motion and interaction in a Hele-Shaw cell. J. Fluid Mech. 173, 95–114.Google Scholar
Pompano, R. R., Liu, W., Du, W. & Ismagilov, R. F. 2011 Microfluidics using spatially defined arrays of droplets in one, two, and three dimensions. Annu. Rev. Anal. Chem. 4 (1), 59–81.Google Scholar
Prosperetti, A. 2011 Advanced Mathematics for Applications. Cambridge University Press.Google Scholar
Saffman, P. G. & Taylor, G. 1958 The penetration of a fluid into a porous medium or Hele-Shaw cell containing a more viscous liquid. Proc. R. Soc. Lond. A 245 (1242), 312–329.Google Scholar
Sarig, I., Starosvetsky, Y. & Gat, A. 2016 Interaction forces between microfluidic droplets in a Hele-Shaw cell. J. Fluid Mech. 800, 264–277.Google Scholar
Shani, I., Beatus, T., Bar-Ziv, R. H. & Tlusty, T. 2014 Long-range orientational order in two-dimensional microfluidic dipoles. Nat. Phys. 10 (2), 140–144.Google Scholar
Shen, B., Leman, M., Reyssat, M. & Tabeling, P. 2014 Dynamics of a small number of droplets in microfluidic Hele-Shaw cells. Exp. Fluids 55 (5), 1728.Google Scholar
Squires, T. M. & Quake, S. R. 2005 Microfluidics: fluid physics at the nanoliter scale. Rev. Mod. Phys. 77 (3), 977–1026.Google Scholar
Stone, H. A., Stroock, A. D. & Ajdari, A. 2004 Engineering flows in small devices: microfluidics toward a lab-on-a-chip. Annu. Rev. Fluid Mech. 36 (1), 381–411.Google Scholar
Tanveer, S. 1986 The effect of surface tension on the shape of a Hele-Shaw cell bubble. Phys. Fluids 29 (11), 3537–3548.Google Scholar
Taylor, G. & Saffman, P. G. 1959 A note on the motion of bubbles in a Hele-Shaw cell and porous medium. Q. J. Mech. Appl. Maths 12 (3), 265–279.Google Scholar
Teletzke, G. F., Davis, H. T. & Scriven, L. E. 1988 Wetting hydrodynamics. Rev. Phys. Appl. 23 (6), 989–1007.Google Scholar
Uspal, W. E. & Doyle, P. S. 2012a Collective dynamics of small clusters of particles flowing in a quasi-two-dimensional microchannel. Soft Matt. 8 (41), 10676–10686.Google Scholar
Uspal, W. E. & Doyle, P. S. 2012b Scattering and nonlinear bound states of hydrodynamically coupled particles in a narrow channel. Phys. Rev. E 85 (1), 016325.Google Scholar