Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-28T17:20:52.754Z Has data issue: false hasContentIssue false
  • English
  • Français

Analysis of degenerate mechanisms triggering finite-amplitude thermo-acoustic oscillations in annular combustors

Published online by Cambridge University Press:  24 October 2019

Sandeep R. Murthy Open the ORCID record for Sandeep R. Murthy [Opens in a new window] ,
Taraneh Sayadi ,
Vincent Le Chenadec Open the ORCID record for Vincent Le Chenadec [Opens in a new window] ,
Peter J. Schmid Open the ORCID record for Peter J. Schmid [Opens in a new window]  and
Daniel J. Bodony Open the ORCID record for Daniel J. Bodony [Opens in a new window]
Sandeep R. Murthy*
Affiliation:
Department of Aerospace Engineering, University of Illinois at Urbana-Champaign, Urbana, USA
Taraneh Sayadi
Affiliation:
Jean le Rond d’Alembert Institute, Sorbonne University, 75252 Paris CEDEX 05, France
Vincent Le Chenadec
Affiliation:
Multi-Scale Modeling and Simulation Laboratory, University of Paris-Est, 77454 Marne-la-Vallée CEDEX 2, France
Peter J. Schmid
Affiliation:
Department of Mathematics, Imperial College London, London SW7 2AZ, UK
Daniel J. Bodony
Affiliation:
Department of Aerospace Engineering, University of Illinois at Urbana-Champaign, Urbana, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A simplified model is introduced to study finite-amplitude thermo-acoustic oscillations in 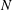$N$-periodic annular combustion devices. Such oscillations yield undesirable effects and can be triggered by a positive feedback between heat-release and pressure fluctuations. The proposed model, comprising the governing equations linearized in the acoustic limit, and with each burner modelled as a one-dimensional system with acoustic damping and a compact heat source, is used to study the instability caused by cross-sector coupling. The coupling between the sectors is included by solving the one-dimensional acoustic jump conditions at the locations where the burners are coupled to the annular chambers of the combustion device. The analysis takes advantage of the block-circulant structure of the underlying stability equations to develop an efficient methodology to describe the onset of azimuthally synchronized motion. A modal analysis reveals the dominance of global instabilities (encompassing the large-scale dynamics of the entire system), while a non-modal analysis reveals a strong response to harmonic excitation at forcing frequencies far from the eigenfrequencies, when the overall system is linearly stable. In all presented cases, large-scale, azimuthally synchronized (coupled) motion is observed. The relevance of the non-modal response is further emphasized by demonstrating the subcritical nature of the system’s Hopf point via an asymptotic expansion of a nonlinear model representing the compact heat source within each burner.

JFM classification

Instability: Nonlinear instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 881 , 25 December 2019 , pp. 384 - 419
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ananthkrishnan, N., Deo, S. & Culick, F. E. C. 2005 Reduced-order modeling and dynamics of nonlinear acoustic waves in a combustion chamber. Combust. Sci. Technol. 177 (2), 221–248.Google Scholar
Balasubramanian, K. & Sujith, R. I. 2008 Thermoacoustic instability in a Rijke tube: Non-normality and nonlinearity. Phys. Fluids 20 (4), 044103.Google Scholar
Balasubramanian, K. & Sujith, R. I. 2013 Non-normality and nonlinearity in combustionacoustic interaction in diffusion flames corrigendum. J. Fluid Mech. 733, 680.Google Scholar
Bauerheim, M., Parmentier, J.-F., Salas, P., Nicoud, F. & Poinsot, T. 2014 An analytical model for azimuthal thermoacoustic modes in an annular chamber fed by an annular plenum. Combust. Flame 161 (5), 1374–1389.Google Scholar
Bourgouin, J.-F., Durox, D., Moeck, J. P., Schuller, T. & Candel, S. 2015 Characterization and modeling of a spinning thermoacoustic instability in an annular combustor equipped with multiple matrix injectors. Trans. ASME J. Engng Gas Turbines Power 137 (2), 021503.Google Scholar
Candel, S. 1992 Combustion instabilities coupled by pressure waves and their active control. In Symposium (International) on Combustion, vol. 24, pp. 1277–1296. Elsevier.Google Scholar
Candel, S., Durox, D. & Schuller, T. 2004 Flame interactions as a source of noise and combustion instabilities. In 10th AIAA/CEAS Aeroacoustics Conference, 10–12 May, Manchester, UK. AIAA Paper 2004-2928.Google Scholar
Candel, S., Maistret, E., Darabiha, N., Poinsot, T., Veynante, D. & Lacas, F. 1988 Experimental and numerical studies of turbulent ducted flames. In Marble Symposium in Caltech, August, Pasadena, CA, USA. Marble Symposium Paper 1988-209.Google Scholar
Clavin, P., Pelcé, P. & He, L. 1990 One-dimensional vibratory instability of planar flames propagating in tubes. J. Fluid Mech. 216, 299–322.Google Scholar
Culick, F. E. C. 1989 Combustion instabilities in liquid-fueled propulsion systems an overview. In AGARD Conference Proceedings 450. NATO ASI Series Publication Coordination Office.Google Scholar
Culick, F. E. C. & Kuentzmann, P.2006 Unsteady motions in combustion chambers for propulsion systems. Tech. Rep. DTIC Document.Google Scholar
Dowling, A. P. 1995 The calculation of thermoacoustic oscillations. J. Sound Vib. 180 (4), 557–581.Google Scholar
Ducruix, S., Schuller, T., Durox, D. & Candel, S. 2005 Combustion instability mechanisms in premixed combustors. Progr. Astron. Aeron. 210, 179–212.Google Scholar
Engelborghs, K., Luzyanina, T. & Samaey, G. 2000 DDE-BIFTOOL: a Matlab package for bifurcation analysis of delay differential equations. TW Report 305, 1–36.Google Scholar
Fedkiw, R. P., Aslam, T., Merriman, B. & Osher, S. 1999 A non-oscillatory Eulerian approach to interfaces in multimaterial flows (the Ghost Fluid Method). J. Comput. Phys. 152 (2), 457–492.Google Scholar
Gelbert, G., Moeck, J. P., Paschereit, C. O. & King, R. 2012 Feedback control of unstable thermoacoustic modes in an annular Rijke tube. Control Engng Pract. 20 (8), 770–782.Google Scholar
Ghirardo, G., Di Giovine, C., Moeck, J. P. & Bothien, M. R. 2019 Thermoacoustics of can-annular combustors. Trans. ASME J. Engng Gas Turbines Power 141 (1), 011007.Google Scholar
Ghirardo, G., Juniper, M. P. & Moeck, J. P. 2015 Stability criteria for standing and spinning waves in annular combustors. In ASME Turbo Expo 2015: Turbine Technical Conference and Exposition, p. V04BT04A005. American Society of Mechanical Engineers.Google Scholar
Ghirardo, G., Juniper, M. P. & Moeck, J. P. 2016 Weakly nonlinear analysis of thermoacoustic instabilities in annular combustors. J. Fluid Mech. 805, 52–87.Google Scholar
Harrje, D. T.1972 Liquid propellant rocket combustion instability. Tech. Rep. NASA-SP-194. NASA.Google Scholar
Jahnke, C. C. & Culick, F. E. C. 1994 Application of dynamical systems theory to nonlinear combustion instabilities. J. Propul. Power 10 (4), 508–517.Google Scholar
Jarlebring, E.2008 The spectrum of delay-differential equations: computational analysis. PhD thesis, Inst. Comp. Math., TU Braunschweig, Germany.Google Scholar
Jegadeesan, V. & Sujith, R. I. 2013 Experimental investigation of noise induced triggering in thermoacoustic systems. Proc. Combust. Inst. 34 (2), 3175–3183.Google Scholar
Juniper, M. P. 2011 Triggering in the horizontal Rijke tube: non-normality, transient growth and bypass transition. J. Fluid Mech. 667, 272–308.Google Scholar
Juniper, M. P. 2012 Weakly nonlinear analysis of thermoacoustic oscillations. In 19th International Congress on Sound and Vibration, pp. 1–5. IIAV.Google Scholar
Kabiraj, L. & Sujith, R. I. 2012 Nonlinear self-excited thermoacoustic oscillations: intermittency and flame blowout. J. Fluid Mech. 713, 376–397.Google Scholar
Kopitz, J., Huber, A., Sattelmayer, T. & Polifke, W. 2005 Thermoacoustic stability analysis of an annular combustion chamber with acoustic low order modeling and validation against experiment. In ASME Turbo Expo 2005: Power for Land, Sea, and Air, pp. 583–593. American Society of Mechanical Engineers.Google Scholar
Laera, D., Campa, G. & Camporeale, S. M. 2017 A finite element method for a weakly nonlinear dynamic analysis and bifurcation tracking of thermo-acoustic instability in longitudinal and annular combustors. Appl. Energy 187, 216–227.Google Scholar
Lee, D. S. & Anderson, T. J. 1999 Measurements of fuel/air-acoustic coupling in lean premixed combustion systems. In 37th AIAA Aerospace Sciences Meeting and Exhibit, 11–14 January, Reno, NV, USA. AIAA Paper 1999-0450.Google Scholar
Lee, D.-H. & Lieuwen, T. C. 2003 Premixed flame kinematics in a longitudinal acoustic field. J. Prop. Power 19 (5), 837–846.Google Scholar
Lieuwen, T. C. & Yang, V. 2005 Combustion Instabilities in Gas Turbine Engines: Operational Experience, Fundamental Mechanisms, and Modeling. American Institute of Aeronautics and Astronautics.Google Scholar
Lord Rayleigh 1878 The explanation of certain acoustical phenomena. R. Inst. Proc. 8, 536–542.Google Scholar
Mariappan, S., Sujith, R. I. & Schmid, P. J. 2011 Non-normality of thermoacoustic interactions: an experimental investigation. In 47th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, 31 July–3 August, San Diego, CA, USA. AIAA Paper 2011-5555.Google Scholar
Mensah, G. A., Campa, G. & Moeck, J. P. 2016 Efficient computation of thermoacoustic modes in industrial annular combustion chambers based on Bloch-wave theory. Trans. ASME J. Engng Gas Turbines Power 138 (8), 081502.Google Scholar
Mensah, G. A., Magri, L., Orchini, A. & Moeck, J. P. 2019 Effects of asymmetry on thermoacoustic modes in annular combustors: a higher-order perturbation study. Trans. ASME J. Engng Gas Turbines Power 141 (4), 041030.Google Scholar
Mensah, G. A. & Moeck, J. P. 2015 Efficient computation of thermoacoustic modes in annular combustion chambers based on Bloch-wave theory. In ASME Turbo Expo 2015: Turbine Technical Conference and Exposition, p. V04BT04A036. American Society of Mechanical Engineers.Google Scholar
Moeck, J. P., Paul, M. & Paschereit, C. O. 2010 Thermoacoustic instabilities in an annular Rijke tube. In ASME Turbo Expo 2010: Power for Land, Sea, and Air, pp. 1219–1232. American Society of Mechanical Engineers.Google Scholar
Newell, A. C. & Whitehead, J. A. 1969 Finite bandwidth, finite amplitude convection. J. Fluid Mech. 38 (2), 279–303.Google Scholar
Nicoud, F. & Poinsot, T. 2005 Thermoacoustic instabilities: Should the Rayleigh criterion be extended to include entropy changes? Combust. Flame 142 (1), 153–159.Google Scholar
Noiray, N., Bothien, M. & Schuermans, B. 2011 Investigation of azimuthal staging concepts in annular gas turbines. Combust. Theor. Model. 15 (5), 585–606.Google Scholar
Noiray, N., Durox, D., Schuller, T. & Candel, S. 2008 A unified framework for nonlinear combustion instability analysis based on the flame describing function. J. Fluid Mech. 615, 139–167.Google Scholar
Noiray, N. & Schuermans, B. 2013 On the dynamic nature of azimuthal thermoacoustic modes in annular gas turbine combustion chambers. Proc. R. Soc. Lond. A 469 (2151), 20120535.Google Scholar
Oden, J. T. & Demkowicz, L. 2017 Applied Functional Analysis. CRC press.Google Scholar
Orchini, A., Mensah, G. A. & Moeck, J. P. 2019 Effects of nonlinear modal interactions on the thermoacoustic stability of annular combustors. Trans. ASME J. Engng Gas Turbines Power 141 (2), 021002.Google Scholar
Orchini, A., Rigas, G. & Juniper, M. P. 2016 Weakly nonlinear analysis of thermoacoustic bifurcations in the Rijke tube. J. Fluid Mech. 805, 523–550.Google Scholar
Parmentier, J.-F., Salas, P., Wolf, P., Staffelbach, G., Nicoud, F. & Poinsot, T. 2012 A simple analytical model to study and control azimuthal instabilities in annular combustion chambers. Comb. Flame 159 (7), 2374–2387.Google Scholar
Poinsot, T., Trouve, A. C., Veynante, D. P., Candel, S. & Esposito, E. J. 1987 Vortex-driven acoustically coupled combustion instabilities. J. Fluid Mech. 177, 265–292.Google Scholar
Poinsot, T. & Veynante, D. 2005 Theoretical and Numerical Combustion. RT Edwards, Inc.Google Scholar
Polifke, W., Paschereit, C. O. & Döbbeling, K. 2001 Constructive and destructive interference of acoustic and entropy waves in a premixed combustor with a choked exit. Intl J. Acoust. Vib. 6 (3), 135–146.Google Scholar
Salas, P.2013 Aspects numériques et physiques des instabilités thermoacoustiques dans les chambres de combustion annulaire. PhD thesis, Université Bordeaux I, Bordeaux, France.Google Scholar
Sattelmayer, T. & Polifke, W. 2003 Assessment of methods for the computation of the linear stability of combustors. Combust. Sci. Technol. 175 (3), 453–476.Google Scholar
Sayadi, T., Le Chenadec, V., Schmid, P. J., Richecoeur, F. & Massot, M. 2014 Thermoacoustic instability – a dynamical system and time domain analysis. J. Fluid Mech. 753, 448–471.Google Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows. Springer.Google Scholar
Schmid, P. J., Fosas de Pando, M. & Peake, N. 2017 Stability analysis for n-periodic array of fluid systems. Phys. Rev. Fluids 2 (11), 113902.Google Scholar
Sensiau, C., Nicoud, F. & Poinsot, T. 2008 Computation of azimuthal combustion instabilities in an helicopter combustion chamber. In 14th AIAA/CEAS Aeroacoustics Conference, 5–7 May, Vancouver, British Columbia, Canada. AIAA Paper 2008-2947.Google Scholar
Sipp, D. & Lebedev, A. 2007 Global stability of base and mean flows: a general approach and its applications to cylinder and open cavity flows. J. Fluid Mech. 593, 333–358.Google Scholar
Staffelbach, G., Gicquel, L. Y. M., Boudier, G. & Poinsot, T. 2009 Large eddy simulation of self excited azimuthal modes in annular combustors. Proc. Combust. Inst. 32 (2), 2909–2916.Google Scholar
Stow, S. R. & Dowling, A. P. 2001 Thermoacoustic oscillations in an annular combustor. In ASME Turbo Expo 2001: Power for Land, Sea, and Air, pp. 0037–0045. American Society of Mechanical Engineers.Google Scholar
Subramanian, P., Sujith, R. I. & Wahi, P. 2013 Subcritical bifurcation and bistability in thermoacoustic systems. J. Fluid Mech. 715, 210–238.Google Scholar
Sujith, R. I., Juniper, M. P. & Schmid, P. J. 2016 Non-normality and nonlinearity in thermoacoustic instabilities. Intl J. Spray Combust. Dyn. 8 (2), 119–146.Google Scholar
Trefethen, L. N. 2000 Spectral Methods in MatLab. Society for Industrial and Applied Mathematics.Google Scholar
Wolf, P., Staffelbach, G., Gicquel, L. Y. M., Müller, J.-D. & Poinsot, T. 2012 Acoustic and large eddy simulation studies of azimuthal modes in annular combustion chambers. Combust. Flame 159 (11), 3398–3413.Google Scholar
Worth, N. A. & Dawson, J. R. 2013a Modal dynamics of self-excited azimuthal instabilities in an annular combustion chamber. Combust. Flame 160 (11), 2476–2489.Google Scholar
Worth, N. A. & Dawson, J. R. 2013b Self-excited circumferential instabilities in a model annular gas turbine combustor: global flame dynamics. Proc. Combust. Inst. 34 (2), 3127–3134.Google Scholar