Article contents
Analogies and differences between the stability of an isolated pancake vortex and a columnar vortex in stratified fluid
Published online by Cambridge University Press: 11 May 2016
Abstract
In order to understand the dynamics of pancake shaped vortices in stably stratified fluids, we perform a linear stability analysis of an axisymmetric vortex with Gaussian angular velocity in both the radial and axial directions with an aspect ratio of  ${\it\alpha}$. The results are compared to those for a columnar vortex (
${\it\alpha}$. The results are compared to those for a columnar vortex (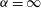 ${\it\alpha}=\infty$) in order to identify the instabilities. Centrifugal instability occurs when
${\it\alpha}=\infty$) in order to identify the instabilities. Centrifugal instability occurs when 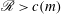 $\mathscr{R}>c(m)$ where
$\mathscr{R}>c(m)$ where 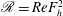 $\mathscr{R}=ReF_{h}^{2}$ is the buoyancy Reynolds number,
$\mathscr{R}=ReF_{h}^{2}$ is the buoyancy Reynolds number, 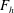 $F_{h}$ the Froude number,
$F_{h}$ the Froude number, 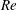 $Re$ the Reynolds number and
$Re$ the Reynolds number and 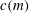 $c(m)$ a constant which differs for the three unstable azimuthal wavenumbers
$c(m)$ a constant which differs for the three unstable azimuthal wavenumbers 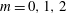 $m=0,1,2$. The maximum growth rate depends mostly on
$m=0,1,2$. The maximum growth rate depends mostly on 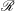 $\mathscr{R}$ and is almost independent of the aspect ratio
$\mathscr{R}$ and is almost independent of the aspect ratio  ${\it\alpha}$. For sufficiently large buoyancy Reynolds number, the axisymmetric mode is the most unstable centrifugal mode whereas for moderate
${\it\alpha}$. For sufficiently large buoyancy Reynolds number, the axisymmetric mode is the most unstable centrifugal mode whereas for moderate 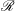 $\mathscr{R}$, the mode
$\mathscr{R}$, the mode 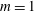 $m=1$ is the most unstable. Shear instability for
$m=1$ is the most unstable. Shear instability for 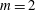 $m=2$ develops only when
$m=2$ develops only when 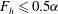 $F_{h}\leqslant 0.5{\it\alpha}$. By considering the characteristics of shear instability for a columnar vortex with the same parameters, this condition is shown to be such that the vortex is taller than the minimum wavelength of shear instability in the columnar case. For larger Froude number
$F_{h}\leqslant 0.5{\it\alpha}$. By considering the characteristics of shear instability for a columnar vortex with the same parameters, this condition is shown to be such that the vortex is taller than the minimum wavelength of shear instability in the columnar case. For larger Froude number 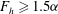 $F_{h}\geqslant 1.5{\it\alpha}$, the isopycnals overturn and gravitational instability can operate. Just below this threshold, the azimuthal wavenumbers
$F_{h}\geqslant 1.5{\it\alpha}$, the isopycnals overturn and gravitational instability can operate. Just below this threshold, the azimuthal wavenumbers 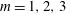 $m=1,2,3$ are unstable to baroclinic instability. A simple model shows that baroclinic instability develops only above a critical vertical Froude number
$m=1,2,3$ are unstable to baroclinic instability. A simple model shows that baroclinic instability develops only above a critical vertical Froude number 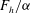 $F_{h}/{\it\alpha}$ because of confinement effects.
$F_{h}/{\it\alpha}$ because of confinement effects.
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 12
- Cited by



