Published online by Cambridge University Press: 12 December 2016
Under Stokesian conditions, a neutrally buoyant non-Brownian spheroid in simple shear flow rotates indefinitely in any of a one-parameter family of closed (Jeffery) orbits characterized by an orbit constant 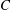 $C$. The limiting values,
$C$. The limiting values, 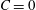 $C=0$ and
$C=0$ and 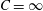 $C=\infty$, correspond to spinning and tumbling modes respectively. Hydrodynamics alone does not determine the distribution of spheroid orientations across Jeffery orbits in the absence of interactions, and the rheology of a dilute suspension of spheroids remains indeterminate. A combination of inertia and stochastic orientation fluctuations eliminates the indeterminacy. The steady-state Jeffery-orbit distribution arising from a balance of inertia and thermal fluctuations is shown to be of the Boltzmann equilibrium form, with a potential that depends on
$C=\infty$, correspond to spinning and tumbling modes respectively. Hydrodynamics alone does not determine the distribution of spheroid orientations across Jeffery orbits in the absence of interactions, and the rheology of a dilute suspension of spheroids remains indeterminate. A combination of inertia and stochastic orientation fluctuations eliminates the indeterminacy. The steady-state Jeffery-orbit distribution arising from a balance of inertia and thermal fluctuations is shown to be of the Boltzmann equilibrium form, with a potential that depends on  $C$, the particle aspect ratio (
$C$, the particle aspect ratio ( $\unicode[STIX]{x1D705}$), and a dimensionless shear rate (
$\unicode[STIX]{x1D705}$), and a dimensionless shear rate (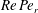 $Re\,Pe_{r}$,
$Re\,Pe_{r}$, 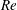 $Re$ and
$Re$ and 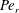 $Pe_{r}$ being the Reynolds and rotary Péclet numbers), and therefore lends itself to a novel thermodynamic interpretation in
$Pe_{r}$ being the Reynolds and rotary Péclet numbers), and therefore lends itself to a novel thermodynamic interpretation in 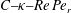 $C{-}\unicode[STIX]{x1D705}{-}Re\,Pe_{r}$ space. In particular, the transition of the potential from a single to a double-well structure, below a critical
$C{-}\unicode[STIX]{x1D705}{-}Re\,Pe_{r}$ space. In particular, the transition of the potential from a single to a double-well structure, below a critical  $\unicode[STIX]{x1D705}$, has similarities to a thermodynamic phase transition, and the small-
$\unicode[STIX]{x1D705}$, has similarities to a thermodynamic phase transition, and the small- $C$ and large-
$C$ and large-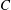 $C$ minima are therefore identified with spinning and tumbling phases. The hysteretic dynamics within the two-phase tumbling–spinning envelope renders the rheology sensitively dependent on the precise shear rate history, the signature in simple shear flow being a multivalued viscosity at a given shear rate. The tumbling–spinning transition identified here is analogous to the coil–stretch transition in the polymer physics literature. It should persist under more general circumstances, and has implications for the suspension stress response in inhomogeneous shearing flows.
$C$ minima are therefore identified with spinning and tumbling phases. The hysteretic dynamics within the two-phase tumbling–spinning envelope renders the rheology sensitively dependent on the precise shear rate history, the signature in simple shear flow being a multivalued viscosity at a given shear rate. The tumbling–spinning transition identified here is analogous to the coil–stretch transition in the polymer physics literature. It should persist under more general circumstances, and has implications for the suspension stress response in inhomogeneous shearing flows.