Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kondakov, Vasily G.
Karabasov, Sergey A.
and
Goloviznin, Vasily
2013.
On the effect of Mach number on subsonic jet noise sources in the Goldstein acoustic analogy model.
Faranosov, Georgy A.
Goloviznin, Vasily M.
Karabasov, Sergey A.
Kondakov, Vasily G.
Kopiev, Victor F.
and
Zaitsev, Mihail A.
2013.
CABARET method on unstructured hexahedral grids for jet noise computation.
Computers & Fluids,
Vol. 88,
Issue. ,
p.
165.
Lele, Sanjiva K.
and
Nichols, Joseph W.
2014.
A second golden age of aeroacoustics?.
Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 372,
Issue. 2022,
p.
20130321.
Semiletov, Vasily
and
Karabasov, Sergey A.
2014.
Adjoint Linearised Euler solver for Goldstein acoustic analogy equations for 3D non-uniform flow sound scattering problems: verification and capability study.
Engel, Rafael C.
Silva, Carlos R.I.
and
Deschamps, Cesar J.
2014.
Application of RANS-based method to predict acoustic noise of chevron nozzles.
Applied Acoustics,
Vol. 79,
Issue. ,
p.
153.
Kreitzman, Jordan R.
and
Nichols, Joseph W.
2015.
Acoustic source analysis of a supersonic rectangular chevron jet.
Sun, Chunhua
Ning, Zhi
Lv, Ming
Yan, Kai
and
Fu, Juan
2015.
Time–frequency analysis of acoustic and unsteadiness evaluation in effervescent sprays.
Chemical Engineering Science,
Vol. 127,
Issue. ,
p.
115.
Karabasov, Sergey A.
and
Sandberg, Richard D.
2015.
Influence of Free Stream Effects on Jet Noise Generation and Propagation within the Goldstein Acoustic Analogy Approach for Fully Turbulent Jet Inflow Boundary Conditions.
International Journal of Aeroacoustics,
Vol. 14,
Issue. 3-4,
p.
413.
Semiletov, Vasily
Karabasov, Sergey A.
Chintagunta, Abhishek
and
Markesteijn, Anton P.
2015.
Empiricism-free noise calculation from LES solution based on Goldstein generalized acoustic analogy: volume noise sources and meanflow effects.
Korolev, Yury
Karabasov, Sergey A.
and
Toropov, Vassili
2015.
Automatic Optimizer vs Human Optimizer for Low-Order Jet Noise Modelling.
Semiletov, Vasily A
and
Karabasov, Sergey A
2017.
Similarity scaling of jet noise sources for low-order jet noise modelling based on the Goldstein generalised acoustic analogy.
International Journal of Aeroacoustics,
Vol. 16,
Issue. 6,
p.
476.
Markesteijn, Anton P.
Semiletov, Vasily
Karabasov, Sergey A.
Tan, Dominic J.
Wong, Marcus
Honnery, Damon
and
Edgington-Mitchell, Daniel M.
2017.
Supersonic Jet Noise: an Investigation into Noise Generation Mechanisms using Large Eddy Simulation and High-Resolution PIV Data.
Leib, Stewart J.
Ingraham, Daniel
and
Bridges, James E.
2017.
Evaluating Source Terms of the Generalized Acoustic Analogy using the Jet Engine Noise REduction (JENRE) Code.
Goldstein, M. E.
and
Leib, S. J.
2018.
Azimuthal Source Noncompactness and Mode Coupling in Sound Radiation from High-Speed Axisymmetric Jets.
AIAA Journal,
Vol. 56,
Issue. 10,
p.
3915.
Semiletov, Vasily A.
and
Karabasov, Sergey A.
2018.
A volume integral implementation of the Goldstein generalised acoustic analogy for unsteady flow simulations.
Journal of Fluid Mechanics,
Vol. 853,
Issue. ,
p.
461.
Afsar, Mohammed Z.
Sescu, Adrian
and
Leib, Stewart J.
2019.
Modelling and prediction of the peak-radiated sound in subsonic axisymmetric air jets using acoustic analogy-based asymptotic analysis.
Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 377,
Issue. 2159,
p.
20190073.
Markesteijn, A. P.
and
Karabasov, S. A.
2019.
Simulations of co-axial jet flows on graphics processing units: the flow and noise analysis.
Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 377,
Issue. 2159,
p.
20190083.
Afsar, M. Z.
Sescu, A.
and
Sassanis, V.
2019.
Effect of non-parallel mean flow on the acoustic spectrum of heated supersonic jets: Explanation of “jet quietening”.
Physics of Fluids,
Vol. 31,
Issue. 10,
Markesteijn, Anton P.
Gryazev, Vasily
Karabasov, Sergey A.
Ayupov, Ruslan Sh.
Benderskiy, Leonid A.
and
Lyubimov, Dmitriy A.
2020.
Flow and Noise Predictions of Coaxial Jets.
AIAA Journal,
Vol. 58,
Issue. 12,
p.
5280.
Spieser, Étienne
and
Bailly, Christophe
2020.
Sound propagation using an adjoint-based method.
Journal of Fluid Mechanics,
Vol. 900,
Issue. ,
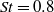 $\mathit{St}= 0. 8$ to
$\mathit{St}= 0. 8$ to 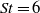 $\mathit{St}= 6$, which was shown to best correspond to the validity range of the acoustic source model for the LES data available, is found between noise predictions using the acoustic analogy model and those of a previously conducted LES–ILEE (isotropic linearized Euler equation) control surface method for the nominally laminar inflow jet case. The acoustic analogy is used to determine the source length scales which contribute to noise at different radiated angles to the jet, how they are distributed and how they change with change of inflow conditions. For the vortex pairing frequency, using a new acoustic source decomposition technique based on the correlation length scale, two types of noise sources are found. One source, which corresponds to the peak source amplitude, is located at the upstream end of the jet and is associated with the vortex pairing. The other one, which is the dominant source, is associated with jet mixing at the end of the jet potential core. It is also shown that boundary layer forcing leads to a reduction in the contribution to the noise of the large source length scales in comparison with the fully laminar case.
$\mathit{St}= 6$, which was shown to best correspond to the validity range of the acoustic source model for the LES data available, is found between noise predictions using the acoustic analogy model and those of a previously conducted LES–ILEE (isotropic linearized Euler equation) control surface method for the nominally laminar inflow jet case. The acoustic analogy is used to determine the source length scales which contribute to noise at different radiated angles to the jet, how they are distributed and how they change with change of inflow conditions. For the vortex pairing frequency, using a new acoustic source decomposition technique based on the correlation length scale, two types of noise sources are found. One source, which corresponds to the peak source amplitude, is located at the upstream end of the jet and is associated with the vortex pairing. The other one, which is the dominant source, is associated with jet mixing at the end of the jet potential core. It is also shown that boundary layer forcing leads to a reduction in the contribution to the noise of the large source length scales in comparison with the fully laminar case.