Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Limbourg, Raphaël
and
Nedić, Jovan
2021.
On the asymptotic matching procedure predicting the formation number.
Physics of Fluids,
Vol. 33,
Issue. 11,
Limbourg, Raphaël
and
Nedić, Jovan
2021.
An extended model for orifice starting jets.
Physics of Fluids,
Vol. 33,
Issue. 6,
Choi, Daehyun
and
Park, Hyungmin
2022.
Flow–structure interaction of a starting jet through a flexible circular nozzle.
Journal of Fluid Mechanics,
Vol. 949,
Issue. ,
Baskaran, Mrudhula
and
Mulleners, Karen
2022.
Lagrangian analysis of bio-inspired vortex ring formation.
Flow,
Vol. 2,
Issue. ,
2023.
The circulation growth of non-impulsive starting jet.
Physics of Fluids,
Vol. 35,
Issue. 5,
Francescangeli, Diego
and
Mulleners, Karen
2023.
Strength and timing of primary and secondary vortices generated by a rotating plate.
Experiments in Fluids,
Vol. 64,
Issue. 7,
Barrere, N.
Brum, J.
Anzibar, M.
Rinderknecht, F.
Sarasúa, L. G.
and
Cabeza, C.
2023.
Lagrangian mixing of pulsatile flows in constricted tubes.
Physics of Fluids,
Vol. 35,
Issue. 2,
Chen, Hongsheng
2023.
Granular vortex ring formed by penetration into loose granular medium: Structure identification.
Communications in Nonlinear Science and Numerical Simulation,
Vol. 127,
Issue. ,
p.
107542.
Chashechkin, Yuli D.
and
Ilinykh, Andrey Yu.
2023.
Intrusive and Impact Modes of a Falling Drop Coalescence with a Target Fluid at Rest.
Axioms,
Vol. 12,
Issue. 4,
p.
374.
2024.
Measurement in Fluid Mechanics.
p.
436.
Gao, Lei
Wang, Xin
and
Yu, Simon C. M.
2024.
Propulsive characteristics of single-pulsed jets with tube and orifice openings.
Physics of Fluids,
Vol. 36,
Issue. 1,
Zheng, Haojun
Gao, Lei
and
Yu, Simon C.M.
2025.
Formation process of a two-dimensional starting jet.
Journal of Fluid Mechanics,
Vol. 1007,
Issue. ,
Goyal, A.
and
Nedić, J.
2025.
Starting vortex strength in an impulsively started airfoil.
Physics of Fluids,
Vol. 37,
Issue. 3,
Li, Jin-Feng
Zhang, Xiao-Bing
and
New, T. H.
2025.
Formation and flow characteristics of low-Reynolds number synthetic jets.
Physics of Fluids,
Vol. 37,
Issue. 3,
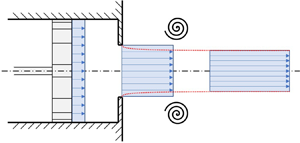
 $D_0/D_p$ is studied using time-resolved particle image velocimetry. The invariants of the motion in their non-dimensional form are computed and presented in the non-dimensional time space
$D_0/D_p$ is studied using time-resolved particle image velocimetry. The invariants of the motion in their non-dimensional form are computed and presented in the non-dimensional time space  $t^*=U_0 t/D_0$, where the subscript 0 refers to the exhaust quantities. The classic slug-flow model is revisited and extended to account for the contraction of the flow when fluid is being pushed out through the orifice. Accordingly, a new time scale in terms of the contracted quantities (subscript
$t^*=U_0 t/D_0$, where the subscript 0 refers to the exhaust quantities. The classic slug-flow model is revisited and extended to account for the contraction of the flow when fluid is being pushed out through the orifice. Accordingly, a new time scale in terms of the contracted quantities (subscript  $\star$) is defined as
$\star$) is defined as  $T^*=U_\star t/D_\star$. Results show that the modified slug-flow model unifies the formation number of orifices and straight nozzles with a value of approximately 4.
$T^*=U_\star t/D_\star$. Results show that the modified slug-flow model unifies the formation number of orifices and straight nozzles with a value of approximately 4.


