Hostname: page-component-669899f699-7tmb6 Total loading time: 0 Render date: 2025-04-25T13:58:41.768Z Has data issue: false hasContentIssue false
  • English
  • Français

An experimental study of flow near an advancing contact line: a rigorous test of theoretical models

Published online by Cambridge University Press:  29 November 2024

Charul Gupta Open the ORCID record for Charul Gupta [Opens in a new window] ,
Anjishnu Choudhury Open the ORCID record for Anjishnu Choudhury [Opens in a new window] ,
Lakshmana D. Chandrala Open the ORCID record for Lakshmana D. Chandrala [Opens in a new window]  and
Harish N. Dixit Open the ORCID record for Harish N. Dixit [Opens in a new window]
Charul Gupta
Affiliation:
Department of Mechanical & Aerospace Engineering, Indian Institute of Technology Hyderabad, Telangana 502284, India
Anjishnu Choudhury
Affiliation:
PMMH, CNRS, ESPCI Paris, Université PSL, Sorbonne Université, Université de Paris, F-75005 Paris, France
Lakshmana D. Chandrala
Affiliation:
Department of Mechanical & Aerospace Engineering, Indian Institute of Technology Hyderabad, Telangana 502284, India
Harish N. Dixit*
Affiliation:
Department of Mechanical & Aerospace Engineering, Indian Institute of Technology Hyderabad, Telangana 502284, India Center for Interdisciplinary Programs, Indian Institute of Technology Hyderabad, Telangana 502284, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

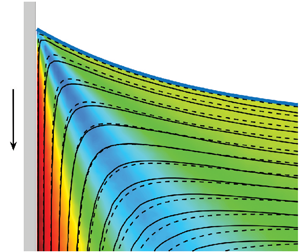
The flow near a moving contact line depends on the dynamic contact angle, viscosity ratio and capillary number. We report experiments involving immersing a plate into a liquid bath, concurrently measuring the interface shape, interfacial velocity and fluid flow using digital image processing and particle image velocimetry. All experiments were performed at low plate speeds to maintain small Reynolds and capillary numbers for comparison with viscous theories. The dynamic contact angle, measured in the viscous phase, was kept below $90^{\circ }$ and the viscosity ratio, $\lambda < 1$. This region of parameter space is largely unexplored for advancing contact lines. An important aim of the present study is to provide new experimental data against which new contact line models can be developed. The flow field is directly compared against the prediction from the viscous theory of Huh & Scriven (J. Colloid Interface Sci., vol. 35, issue 1, 1971, pp. 85–101) but with a slight modification involving the curved interface. Remarkable agreement is found between experiments and theory across a wide parameter range. The prediction for interfacial speed from Huh & Scriven is also in excellent agreement with experiments except in the vicinity of the contact line. Material points along the interface were found to rapidly slow down near the contact line, thus alleviating the singularity at the moving contact line. To the best of our knowledge, such a detailed test of theoretical models has not been performed before and we hope the present study will spur new modelling efforts in the field.

JFM classification

Interfacial Flows (free surface): Contact lines Low-Reynolds-number flows: Lubrication theory Interfacial Flows (free surface): Capillary flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1000 , 10 December 2024 , A45
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Blake, T.D. & Haynes, J.M. 1969 Kinetics of liquid liquid displacement. J. Colloid Interface Sci. 30 (3), 421–423.CrossRefGoogle Scholar
Bonn, D., Eggers, J., Indekeu, J., Meunier, J. & Rolley, E. 2009 Wetting and spreading. Rev. Mod. Phys. 81 (2), 739.CrossRefGoogle Scholar
Chan, T.S., Kamal, C., Snoeijer, J.H., Sprittles, J.E. & Eggers, J. 2020 Cox–Voinov theory with slip. J. Fluid Mech. 900, A8.CrossRefGoogle Scholar
Chan, T.S., Srivastava, S., Marchand, A., Andreotti, B., Biferale, L., Toschi, F. & Snoeijer, J.H. 2013 Hydrodynamics of air entrainment by moving contact lines. Phys. Fluids 25 (7), 074105.CrossRefGoogle Scholar
Chen, Q., Ramé, E. & Garoff, S. 1997 The velocity field near moving contact lines. J. Fluid Mech. 337, 49–66.CrossRefGoogle Scholar
Cox, R.G. 1986 The dynamics of the spreading of liquids on a solid surface. Part 1. Viscous flow. J. Fluid Mech. 168, 169–194.CrossRefGoogle Scholar
De Gennes, P.-G. 1985 Wetting: statics and dynamics. Rev. Mod. Phys. 57 (3), 827.CrossRefGoogle Scholar
Dussan V., E.B. 1976 The moving contact line: the slip boundary condition. J. Fluid Mech. 77, 665–684.CrossRefGoogle Scholar
Dussan V., E.B. & Davis, S.H. 1974 On the motion of a fluid interface along a solid surface. J. Fluid Mech. 65 (1), 7195.CrossRefGoogle Scholar
Dussan V., E.B., Ramé, E. & Garoff, S. 1991 On identifying the appropriate boundary conditions at a moving contact line: an experimental investigation. J. Fluid Mech. 230, 97–116.CrossRefGoogle Scholar
Febres, M. & Legendre, D. 2017 Existence of moffatt vortices at a moving contact line between two fluids. Phys. Rev. Fluids 2 (11), 114002.CrossRefGoogle Scholar
Fuentes, J. & Cerro, R.L. 2005 Flow patterns and interfacial velocities near a moving contact line. Exp. Fluids 38, 503–510.CrossRefGoogle Scholar
Hoffman, R.L. 1975 A study of the advancing interface. I. Interface shape in liquid–gas systems. J. Colloid Interface Sci. 50 (2), 228–241.CrossRefGoogle Scholar
Huh, C. & Scriven, L.E. 1971 Hydrodynamic model of steady movement of a solid/liquid/fluid contact line. J. Colloid Interface Sci. 35 (1), 85–101.CrossRefGoogle Scholar
Joseph, P. & Tabeling, P. 2005 Direct measurement of the apparent slip length. Phys. Rev. E 71 (3), 035303.CrossRefGoogle ScholarPubMed
Kirkinis, E. & Davis, S.H. 2013 Hydrodynamic theory of liquid slippage on a solid substrate near a moving contact line. Phys. Rev. Lett. 110 (23), 234503.CrossRefGoogle Scholar
Kirkinis, E. & Davis, S.H. 2014 Moffatt vortices induced by the motion of a contact line. J. Fluid Mech. 746, R3.CrossRefGoogle Scholar
Kulkarni, Y., Fullana, T. & Zaleski, S. 2023 Stream function solutions for some contact line boundary conditions: Navier slip, super slip and the generalized Navier boundary condition. Proc. R. Soc. A 479 (2278), 20230141.CrossRefGoogle Scholar
Le Grand, N., Daerr, A. & Limat, L. 2005 Shape and motion of drops sliding down an inclined plane. J. Fluid Mech. 541, 293–315.CrossRefGoogle Scholar
Moffatt, H.K. 1964 Viscous and resistive eddies near a sharp corner. J. Fluid Mech. 18 (1), 1–18.CrossRefGoogle Scholar
Ramé, E. & Garoff, S. 1996 Microscopic and macroscopic dynamic interface shapes and the interpretation of dynamic contact angles. J. Colloid Interface Sci. 177 (1), 234–244.CrossRefGoogle ScholarPubMed
Rio, E., Daerr, A., Andreotti, B. & Limat, L. 2005 Boundary conditions in the vicinity of a dynamic contact line: experimental investigation of viscous drops sliding down an inclined plane. Phys. Rev. Lett. 94 (2), 024503.CrossRefGoogle ScholarPubMed
Sheng, P. & Zhou, M. 1992 Immiscible-fluid displacement: contact-line dynamics and the velocity-dependent capillary pressure. Phys. Rev. A 45 (8), 5694.CrossRefGoogle ScholarPubMed
Shikhmurzaev, Y.D. 1993 The moving contact line on a smooth solid surface. Intl J. Multiphase Flow 19 (4), 589–610.CrossRefGoogle Scholar
Shikhmurzaev, Y.D. 1997 Moving contact lines in liquid/liquid/solid systems. J. Fluid Mech. 334, 211–249.CrossRefGoogle Scholar
Sibley, D.N., Nold, A. & Kalliadasis, S. 2015 The asymptotics of the moving contact line: cracking an old nut. J. Fluid Mech. 764, 445–462.CrossRefGoogle Scholar
Snoeijer, J.H. 2006 Free-surface flows with large slopes: beyond lubrication theory. Phys. Fluids 18 (2), 021701.CrossRefGoogle Scholar
Snoeijer, J.H. & Andreotti, B. 2013 Moving contact lines: scales, regimes, and dynamical transitions. Annu. Rev. Fluid Mech. 45, 269–292.CrossRefGoogle Scholar
Supplementary material: File

Gupta et al. supplementary material 1

Gupta et al. supplementary material
Download Gupta et al. supplementary material 1(File)
File 277.2 KB
Supplementary material: File

Gupta et al. supplementary material 2

Gupta et al. supplementary material
Download Gupta et al. supplementary material 2(File)
File 3.6 MB