Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-01-09T22:09:07.806Z Has data issue: false hasContentIssue false
  • English
  • Français

An experimental investigation of divergent bow waves simulated by a two-dimensional plus temporal wave marker technique

Published online by Cambridge University Press:  26 August 2009

MOSTAFA SHAKERI ,
MOHAMMADREZA TAVAKOLINEJAD  and
JAMES H. DUNCAN
MOSTAFA SHAKERI
Affiliation:
Department of Mechanical Engineering, University of Maryland, College Park, MD 20742, USA
MOHAMMADREZA TAVAKOLINEJAD
Affiliation:
Department of Mechanical Engineering, University of Maryland, College Park, MD 20742, USA
JAMES H. DUNCAN*
Affiliation:
Department of Mechanical Engineering, University of Maryland, College Park, MD 20742, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Divergent ship bow waves were simulated experimentally with a two-dimensional wavemaker that employs a flexible wave board. The wavemaker was programmed so that the wave board created a time sequence of shapes that simulated the line of intersection between one side of the hull of a slender ship model moving at constant speed and an imaginary vertical plane oriented normal to the ship model track. The time history of the water surface shape was measured with a cinematic laser-induced fluorescence technique for eight Froude numbers (FD = U/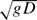, where U is the forward speed of the equivalent three-dimensional ship model, g the acceleration of gravity and D the ship model draft). The waves produced ranged from small-amplitude non-breaking waves at the lowest Froude numbers to plunging breakers at the highest Froude numbers. These waves are strongly forced and at the higher Froude numbers begin breaking before leaving the wave board. The time histories of various geometric characteristics of the water surface shape including the hull contact line, the wave crest, the plunging jet and the splash zone, which is here defined as both the turbulent zone on the front face of the wave in the spilling breakers and the turbulent zone generated ahead of the jet impact point in the plunging breakers, were measured. The phase speed of the primary wave generated during each run ranged from 2.56Uwl (where Uwl is the maximum speed of the wave board at the undisturbed water level in the tank) at the lowest Froude number to about 1.7Uwl at the three highest Froude numbers. The maximum heights of the primary wave, the contact point on the wavemaker and the splash zone increased in a nearly linear fashion with increasing FD. In the cases with plunging jets, the jet tip trajectory was parabolic with a vertical acceleration ranging from 0.6g at FD = 1.467 to 0.8g at FD = 1.817 (the highest Froude number).

Type
Papers
Information
Journal of Fluid Mechanics , Volume 634 , 10 September 2009 , pp. 217 - 243
Copyright
Copyright © Cambridge University Press 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Baba, E. 1969 A new component of viscous resistance of ships. J. Soc. Nav. Arch. Jpn 125, 9–34.CrossRefGoogle Scholar
Bonmarin, P. 1989 Geometric properties of deep-water breaking waves. J. Fluid Mech. 209, 405–433.CrossRefGoogle Scholar
Chen, G. & Kharif, C. 1999 Two-dimensional Navier–Stokes simulation of breaking waves. Phys. Fluids 11 (1), 121–133.CrossRefGoogle Scholar
Dommermuth, D. G., O'Shea, T. T., Wyatt, D. C., Ratcliffe, T., Weymouth, G. D., Hendrikson, K. L., Yue, D. K.-P., Sussman, M., Adams, P. & Valenciano, M. 2007 An application of Cartesian-grid and volume-of-fluid methods to numerical ship hydrodynamics. In Ninth International Conference on Numerical Ship Hydrodynamics, Ann Arbor, MI.Google Scholar
Dommermuth, D. G., O'Shea, T. T., Wyatt, D. C., Sussman, M., Weymouth, G. D. & Yue, D. K. P. 2006 Numerical simulation of ship waves using Cartesian-grid and volume-of-fluid methods. In 26th Symposium on Naval Hydrodynamics, Rome, Italy.Google Scholar
Dong, R. R., Katz, J. & Huang, T. T. 1997 On the structure of bow waves on a ship model. J. Fluid Mech. 346 77–115.CrossRefGoogle Scholar
Landrini, M., Colagrossi, A. & Tulin, M. P. 2001 Breaking bow and stern waves: numerical simulations. In 16th International Workshop on Water Waves and Floating Bodies, Hiroshima, Japan.Google Scholar
Longuet-Higgins, M. S. 1995 On the disintegration of the jet in a plunging breaker. J. Phys. Oceanogr. 25 (10), 2458–2462.2.0.CO;2>CrossRefGoogle Scholar
Miller, R. L. 1976 Role of vortices in surf zone prediction: sedimentation and wave forces. In Beach and Nearshore Sedimentation, pp. 92–113. Society of Economic Paleontologists and Mineralogists, ed. Davis, R. A. and Ethington, R. L..CrossRefGoogle Scholar
Miyata, H. & Inui, T. 1984 Nonlinear ship waves. Adv. Appl. Mech. 24, 215–288.CrossRefGoogle Scholar
New, A. L., McIver, P. & Peregrine, D. H. 1985 Computations of overturning waves. J. Fluid Mech. 150, 233–251.CrossRefGoogle Scholar
Noblesse, F., Delhommeau, G., Guilbaud, M., Hendrix, D. & Yang, C. 2008 Simple analytical relations for ship bow waves. J. Fluid Mech. 600, 105–132.CrossRefGoogle Scholar
Noblesse, F., Hendrix, D., Faul, L. & Slutsky, J. 2006 Simple analytical expressions for the height, location, and steepness of a ship bow wave. J. Ship Res. 50, 360–370.CrossRefGoogle Scholar
Ogilvie, T. F. 1972 The wave generated by a fine ship bow. In Proceedings of the Ninth Symposium on Naval Hydrodynamics (ed. Brard, R. & Castera, C.), pp. 1483–1524. Department of the Navy.Google Scholar
Olivieri, A., Pistani, F., Wilson, R., Campana, E. F. & Stern, F. 2007 Scars and vortices induced by ship bow and shoulder wave breaking. J. Fluids Engng 129, 1445–1459.CrossRefGoogle Scholar
Rapp, R. J. & Melville, W. K. 1990 Laboratory measurements of deep-water breaking waves. Phil. Trans. R. Soc. Lond. A 331, 735–800.Google Scholar
Shakeri, M. 2005 An experimental 2D+T investigation of breaking bow waves. PhD dissertation, Department of Mechanical Engineering, University of Maryland, MD.Google Scholar
Shakeri, M., Maxeiner, E., Fu, T. & Duncan, J. H. 2009 An experimental examination of the 2D+T technique. J. Ship Res. 53 (2), 59–71.CrossRefGoogle Scholar
Song, W. & Maruo, H. 1993 Bow impact and deck wetness: simulations based on nonlinear slender body theory. In Proceedings of the Third International Offshore and Polar Engineering Conference, vol. 3, pp. 34–38. Publisher: International Society of Offshore and Polar Engineers.Google Scholar
Standing, R. G. 1974 Phase and amplitude discrepancies in the surface wave due to a wedge-ended hull form. J. Fluid Mech. 62 625–642.CrossRefGoogle Scholar
Tulin, M. P. 1957 The theory of slender surface planing at high speeds. Schiffstechnik, 4, Heft 21, 125–133.Google Scholar
Tulin, M. P. & Hsu, C. C. 1986 Theory of high speed displacement ships with transom sterns. J. Ship Res. 21-1.Google Scholar
Tulin, M. P. & Wu, M. 1996 Divergent bow waves. In Proceedings of the 21th Symposium on Naval Hydrodynamics, pp. 661–679.Google Scholar
Van Dorn, W. G. & Pazan, S. E. 1975 Laboratory investigation of wave breaking. Part 2. Deep water waves. Rep. 75-21. Scripps Institution of Oceanography. Rep. 71. Advanced Ocean Engineering Laboratory.CrossRefGoogle Scholar
Waniewski, T. A., Brennen, C. E. & Raichlen, F. 2002 Bow wave dynamics. J. Ship Res. 46, 1–15.CrossRefGoogle Scholar
Supplementary material: File

Shakeri supplementary material

Waveboard profiles

Download Shakeri supplementary material(File)
File 101.9 KB