Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-25T13:11:42.380Z Has data issue: false hasContentIssue false
  • English
  • Français

An exceptional point switches stability of a thermoacoustic experiment

Published online by Cambridge University Press:  11 June 2021

Abdulla Ghani Open the ORCID record for Abdulla Ghani [Opens in a new window]  and
Wolfgang Polifke Open the ORCID record for Wolfgang Polifke [Opens in a new window]
Abdulla Ghani*
Affiliation:
Department of Mechanical Engineering and Transport Systems, Technical University of Berlin, 10623Berlin, Germany
Wolfgang Polifke
Affiliation:
Department of Mechanical Engineering, Technical University of Munich, D-85748Garching, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

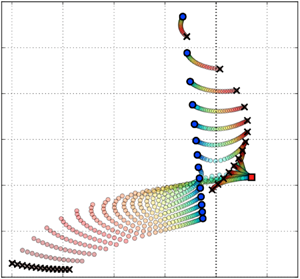
We identify an exceptional point in the numerical stability map of a combustion experiment operated with laminar premixed flames. A low-order model of the experiment allows one to investigate the interplay between the system modes and an exceptional point. The latter is located in the unstable region of the complex eigenvalue plane. Under gradual variation of the operating parameters, the branch-switching characteristic of the exceptional point can facilitate abrupt changes between strong instability and stable operation. The results also indicate that intrinsic thermoacoustic feedback plays an important role in the stability characteristics of this experiment.

JFM classification

Nonlinear Dynamical Systems: Low-dimensional models
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 920 , 10 August 2021 , R3
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Aguilar, J.G & Juniper, M.P. 2020 Thermoacoustic stabilization of a longitudinal combustor using adjoint methods. Phys. Rev. Fluids 5 (8), 083902.CrossRefGoogle Scholar
Albayrak, A., Steinbacher, T., Komarek, T. & Polifke, W. 2018 Convective scaling of intrinsic thermo-acoustic eigenfrequencies of a premixed swirl combustor. Trans. ASME: J. Engng Gas Turbines Power 140 (4), 41–51.Google Scholar
Aurégan, Y. & Pagneux, V. 2017 PT-symmetric scattering in flow duct acoustics. Phys. Rev. Lett. 118 (17), 174301.CrossRefGoogle ScholarPubMed
Bomberg, S., Emmert, T. & Polifke, W. 2015 Thermal versus acoustic response of velocity sensitive premixed flames. Proc. Combust. Inst. 35 (3), 3185–3192.CrossRefGoogle Scholar
Brear, M.J., Nicoud, F., Talei, M., Giauque, A. & Hawkes, E.R. 2012 Disturbance energy transport and sound production in gaseous combustion. J. Fluid Mech. 707, 53–73.CrossRefGoogle Scholar
Candel, S. 2002 Combustion dynamics and control: progress and challenges. Proc. Combust. Inst. 29 (1), 1–28.CrossRefGoogle Scholar
Cartarius, H., Main, J. & Wunner, G. 2007 Exceptional points in atomic spectra. Phys. Rev. Lett. 99 (17), 173003.CrossRefGoogle ScholarPubMed
Chu, B.-T. 1953 On the generation of pressure waves at a plane flame front. Symp. (Intl) Combust. 4 (1), 603–612.CrossRefGoogle Scholar
Courtine, E., Selle, L. & Poinsot, T. 2015 DNS of intrinsic thermoacoustic modes in laminar premixed flames. Combust. Flame 162 (11), 4331–4341.CrossRefGoogle Scholar
Doppler, J., Mailybaev, A.A., Böhm, J., Kuhl, U., Girschik, A., Libisch, F., Milburn, T.J., Rabl, P., Moiseyev, N. & Rotter, S. 2016 Dynamically encircling an exceptional point for asymmetric mode switching. Nature 537 (7618), 76.CrossRefGoogle ScholarPubMed
Dowling, A.P. 1997 Nonlinear self-excited oscillations of a ducted flame. J. Fluid Mech. 346, 271–290.CrossRefGoogle Scholar
Emmert, T., Bomberg, S., Jaensch, S. & Polifke, W. 2017 Acoustic and intrinsic thermoacoustic modes of a premixed combustor. Proc. Combust. Inst. 36 (3), 3835–3842.CrossRefGoogle Scholar
Emmert, T., Bomberg, S. & Polifke, W. 2015 Intrinsic thermoacoustic instability of premixed flames. Combust. Flame 162 (1), 75–85.CrossRefGoogle Scholar
Emmert, T., Meindl, M., Jaensch, S. & Polifke, W. 2016 Linear state space interconnect modeling of acoustic systems. Acta Acust. United Acust. 102 (5), 824–833.CrossRefGoogle Scholar
Feng, L., Wong, Z.J., Ma, R.-M., Wang, Y. & Zhang, X. 2014 Single-mode laser by parity-time symmetry breaking. Science 346 (6212), 972–975.CrossRefGoogle ScholarPubMed
Gavin, B., Miedlar, A. & Polizzi, E. 2018 Feast eigensolver for nonlinear eigenvalue problems. J. Comput. Sci. 27, 107–117.CrossRefGoogle Scholar
Ghani, A. & Poinsot, T. 2017 Flame quenching at walls: A source of sound generation. Flow Turbul. Combust. 99 (1), 173–184.CrossRefGoogle Scholar
Ghani, A., Steinbacher, T., Albayrak, A. & Polifke, W. 2019 Intrinsic thermoacoustic feedback loop in turbulent spray flames. Combust. Flame 205, 22–32.CrossRefGoogle Scholar
Goldzak, T., Mailybaev, A.A. & Moiseyev, N. 2018 Light stops at exceptional points. Phys. Rev. Lett. 120 (1), 013901.CrossRefGoogle ScholarPubMed
Heiss, W.D. 2012 The physics of exceptional points. J. Phys. A 45 (44), 444016.CrossRefGoogle Scholar
Hoeijmakers, M., Kornilov, V., Arteaga, I.L., de Goey, P. & Nijmeijer, H. 2014 Intrinsic instability of flame–acoustic coupling. Combust. Flame 161 (11), 2860–2867.CrossRefGoogle Scholar
Hoeijmakers, M., Kornilov, V., Arteaga, I.L., de Goey, P. & Nijmeijer, H. 2016 Flame dominated thermoacoustic instabilities in a system with high acoustic losses. Combust. Flame 169, 209–215.CrossRefGoogle Scholar
Juniper, M.P. & Sujith, R.I. 2018 Sensitivity and nonlinearity of thermoacoustic oscillations. Annu. Rev. Fluid Mech. 50, 661–689.CrossRefGoogle Scholar
Keller, J.J. 1995 Thermoacoustic oscillations in combustion chambers of gas turbines. AIAA J. 33 (12), 2280–2287.CrossRefGoogle Scholar
Kraus, C., Selle, L. & Poinsot, T. 2018 Coupling heat transfer and large eddy simulation for combustion instability prediction in a swirl burner. Combust. Flame 191, 239–251.CrossRefGoogle Scholar
Latinne, O., Kylstra, N.J., Dörr, M., Purvis, J., Terao-Dunseath, M., Joachain, C.J., Burke, P.G. & Noble, C.J. 1995 Laser-induced degeneracies involving autoionizing states in complex atoms. Phys. Rev. Lett. 74 (1), 46.CrossRefGoogle ScholarPubMed
Levine, H. & Schwinger, J. 1948 On the radiation of sound from an unflanged circular pipe. Phys. Rev. 73 (4), 383.CrossRefGoogle Scholar
Lieuwen, T. & Yang, V. 2005 Combustion instabilities in gas turbine engines. operational experience, fundamental mechanisms and modeling. Progress in Astronautics and Aeronautics, vol. 210. AIAA.Google Scholar
Magri, L. 2019 Adjoint methods as design tools in thermoacoustics. Appl. Mech. Rev. 71 (2), 020801.CrossRefGoogle Scholar
Mensah, G.A., Magri, L., Silva, C.F., Buschmann, P.E. & Moeck, J.P. 2018 Exceptional points in the thermoacoustic spectrum. J. Sound Vib. 433, 124–128.CrossRefGoogle Scholar
Miri, M.-A. & Alu, A. 2019 Exceptional points in optics and photonics. Science 363 (6422), eaar7709.CrossRefGoogle ScholarPubMed
Moeck, J.P., Oevermann, M., Klein, R., Paschereit, C. & Schmidt, H. 2009 A two-way coupling for modeling thermoacoustic instabilities in a flat flame Rijke tube. Proc. Combust. Inst. 32, 1199–1207.CrossRefGoogle Scholar
Morgans, A.S. & Dowling, A.P. 2007 Model-based control of combustion instabilities. J. Sound Vib. 299 (1–2), 261–282.CrossRefGoogle Scholar
Mukherjee, N.K. 2018 Analytic description of flame intrinsic instability in one-dimensional model of open–open combustors with ideal and non-ideal end boundaries. Intl J. Spray Combust. 10 (4), 287–314.CrossRefGoogle Scholar
Munjal, M.L. 1987 Acoustics of ducts and mufflers with application to exhaust and ventilation system design. John Wiley & Sons.Google Scholar
Murugesan, M., Singaravelu, B., Kushwaha, A.K. & Mariappan, S. 2018 Onset of flame-intrinsic thermoacoustic instabilities in partially premixed turbulent combustors. Intl J. Spray Combust. Dyn. 10 (3), 171–184.CrossRefGoogle Scholar
Noiray, N. 2007 Analyse linéaire et non-linéaire des instabilités de combustion: application aux systèmes à injection multipoints et stratégies de contrôle. PhD thesis, Laboratoire d’énergétique moléculaire et macroscopique, combustion (Gif-sur-Yvette, Essonne).Google Scholar
Noiray, N., Durox, D., Schuller, T. & Candel, S. 2007 Passive control of combustion instabilities involving premixed flames anchored on perforated plates. Proc. Combust. Inst. 31, 1283–1290.CrossRefGoogle Scholar
Noiray, N., Durox, D., Schuller, T. & Candel, S. 2008 A unified framework for nonlinear combustion instability analysis based on the flame describing function. J. Fluid Mech. 615, 139–167.CrossRefGoogle Scholar
Orchini, A., Silva, C.F., Mensah, G.A. & Moeck, J.P. 2020 Thermoacoustic modes of intrinsic and acoustic origin and their interplay with exceptional points. Combust. Flame 211, 83–95.CrossRefGoogle Scholar
Poinsot, T. 2017 Prediction and control of combustion instabilities in real engines. Proc. Combust. Inst. 36 (1), 1–28.CrossRefGoogle Scholar
Rayleigh, Lord 1878 The explanation of certain acoustic phenomena. Nature 18, 319–321.CrossRefGoogle Scholar
Schaefer, F., Guo, S. & Polifke, W. 2021 The impact of exceptional points on the reliability of thermoacoustic stability analysis. Trans. ASME: J. Engng Gas Turbines Power 143 (2), 021010.Google Scholar
Schuermans, B. 2003 Modeling and control of thermoacoustic instabilities. PhD thesis, Ecole Polytechnique Federale de Lausanne.Google Scholar
Seyranian, A.P., Kirillov, O.N. & Mailybaev, A.A. 2005 Coupling of eigenvalues of complex matrices at diabolic and exceptional points. J. Phys. A 38 (8), 1723.CrossRefGoogle Scholar
Silva, C., Yong, K.J. & Magri, L. 2019 Thermoacoustic modes of quasi-one-dimensional combustors in the region of marginal stability. Trans. ASME: J. Engng Gas Turbines Power 141 (2), 021022.Google Scholar
Strahle, W.C. 1971 On combustion generated noise. J. Fluid Mech. 49, 399–414.CrossRefGoogle Scholar
Subramanian, P., Blumenthal, R.S., Polifke, W. & Sujith, R.I. 2015 Distributed time lag response functions for the modelling of combustion dynamics. Combust. Theor. Model. 19 (2), 223–237.CrossRefGoogle Scholar
Wiersig, J. 2020 Review of exceptional point-based sensors. Photon. Res. 8 (9), 1457–1467.CrossRefGoogle Scholar