Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-26T15:28:09.576Z Has data issue: false hasContentIssue false
  • English
  • Français

An example where lubrication theory comes short: hydraulic jumps in a flow down an inclined plate

Published online by Cambridge University Press:  29 December 2014

E. S. Benilov  and
V. N. Lapin
E. S. Benilov*
Affiliation:
Department of Mathematics, University of Limerick, Ireland
V. N. Lapin
Affiliation:
School of Mathematics, University of Leeds, Leeds LS2 9JT, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We examine two-dimensional flows of a viscous liquid on an inclined plate. If the upstream depth 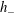$h_{-}$ of the liquid is larger than its downstream depth 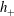$h_{+}$, a smooth hydraulic jump (bore) forms and starts propagating down the slope. If the inclination angle of the plate is small, the bore can be described by the so-called lubrication theory. In this work we demonstrate that bores with 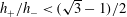$h_{+}/h_{-}<(\sqrt{3}-1)/2$ either are unstable or do not exist as steady solutions of the governing equation (physically, these two possibilities are difficult to distinguish). The instability/evolution occurs near a stagnation point and, generally, causes overturning – sometimes on the scale of the whole bore, sometimes on a shorter, local scale. The overturning occurs because the flow advects disturbances towards the stagnation point and, thus, ‘compresses’ them, increasing the slope of the free surface. Interestingly, this effect is not captured by the lubrication theory, which formally yields a well-behaved stable solution for all values of 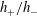$h_{+}/h_{-}$.

JFM classification

Interfacial Flows (free surface): Interfacial Flows (free surface) Low-Reynolds-number flows: Lubrication theory Waves/Free-surface Flows: Wave breaking
Type
Papers
Information
Journal of Fluid Mechanics , Volume 764 , 10 February 2015 , pp. 277 - 295
Check for updates
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bayly, B. J., Holm, D. D. & Lifschitz, A. 1996 Three-dimensional stability of elliptical vortex columns in external strain flows. Phil. Trans. R. Soc. Lond. A 354, 895–950.Google Scholar
Benilov, E. S. 2004 Explosive instability in a linear system with neutrally stable eigenmodes. Part 2. Multi-dimensional disturbances. J. Fluid Mech. 501, 105–124.CrossRefGoogle Scholar
Benilov, E. S. 2014 A depth-averaged model for hydraulic jumps on an inclined plate. Phys. Rev. E 89, 053013.Google Scholar
Benilov, E. S. & Lapin, V. N. 2011 Shock waves in Stokes flows down an inclined plate. Phys. Rev. E 83, 06632.Google ScholarPubMed
Benilov, E. S., Lapin, V. N. & O’Brien, S. B. G. 2012 On rimming flows with shocks. J. Engng. Maths 75, 49–62.CrossRefGoogle Scholar
Benilov, E. S., O’Brien, S. B. G. & Sazonov, I. A. 2003 A new type of instability: explosive disturbances in a liquid film inside a rotating horizontal cylinder. J. Fluid Mech. 497, 201–224.CrossRefGoogle Scholar
Benney, D. J. 1966 Long waves on liquid films. J. Math. Phys. 45, 150–155.CrossRefGoogle Scholar
Bertozzi, A. L. & Brenner, M. P. 1997 Linear stability and transient growth in driven contact lines. Phys. Fluids 9, 530–539.CrossRefGoogle Scholar
Bertozzi, A. L. & Shearer, M. 2000 Existence of undercompressive travelling waves in thin film equations. SIAM J. Math. Anal. 33, 194–213.CrossRefGoogle Scholar
Bertozzi, A. L., Münch, A., Fanton, X. & Cazabat, A. M. 1998 Contact line stability and ‘undercompressive shocks’ in driven thin film flow. Phys. Rev. Lett. 81, 5169–5172.CrossRefGoogle Scholar
Bertozzi, A. L., Münch, A., Shearer, M. & Zumbrun, K. 2001 Stability of compressive and undercompressive thin film travelling waves. Eur. J. Appl. Maths 12, 253–291.CrossRefGoogle Scholar
Chang, H.-C. & Demekhin, E. A. 2002 Complex Waves Dynamics on Thin Films. Elsevier.Google Scholar
Friedlander, S. & Vishik, M. M. 1991 Instability criteria for the flow of an inviscid incompressible fluid. Phys. Rev. Lett. 66, 2204–2206.CrossRefGoogle ScholarPubMed
Homsy, G. M. 1974 Model equations for wavy viscous film flow. Lect. Appl. Math. 15, 191–194.Google Scholar
Jeong, J.-T. & Moffatt, H. K. 1992 Free-surface cusps associated with flow at low Reynolds number. J. Fluid Mech. 241, 1–22.CrossRefGoogle Scholar
Joseph, D. D., Nelson, J., Renardy, M. & Renardy, Y. 1991 Two-dimensional cusped interfaces. J. Fluid Mech. 223, 383–409.CrossRefGoogle Scholar
Kalliadasis, S., Demekhin, E. A., Ruyer-Quil, C. & Velarde, M. G. 2003 Thermocapillary instability and wave formation on a film falling down a uniformly heated plane. J. Fluid Mech. 492, 303–338.CrossRefGoogle Scholar
Leblanc, S. 1997 Stability of stagnation points in rotating flows. Phys. Fluids 9, 3566–3569.CrossRefGoogle Scholar
Lebovitz, N. R. & Lifschitz, A. 1996 Short-wavelength instabilities of Riemann ellipsoids. Phil. Trans. R. Soc. Lond. A 354, 927–950.Google Scholar
Lifschitz, A. 1991 Short wavelength instabilities of incompressible 3-dimensional flows and generation of vorticity. Phys. Lett. A 157, 481–487.CrossRefGoogle Scholar
Lifschitz, A. 1995 On the stability of certain motions of an ideal incompressible fluid. Adv. Pure Appl. Math. 15, 404–436.Google Scholar
Lifschitz, A. & Hameiri, E. 1991 Local stability conditions in fluid dynamics. Phys. Fluids A 3, 2644–2651.CrossRefGoogle Scholar
Lin, S. P. 1974 Finite amplitude side-band stability of a viscous fluid. J. Fluid Mech. 63, 417–429.CrossRefGoogle Scholar
Mavromoustaki, A., Matar, O. K. & Craster, R. V. 2010 Shock-wave solutions in two-layer channel flow. I. One-dimensional flows. Phys. Fluids 22, 112102.CrossRefGoogle Scholar
Mei, C. C. 1966 Nonlinear gravity waves in a thin sheet of viscous fluid. J. Math. Phys. 45, 266–288.CrossRefGoogle Scholar
Mekias, H. & Vanden-Broeck, J.-M. 1991 Subcritical flow with a stagnation point due to a source beneath a free surface. Phys. Fluids 3, 2652–2658.CrossRefGoogle Scholar
Nepomnyashchy, A. A. 1974 Stability of the wavy regimes in the film flowing down an inclined plane. Fluid Dyn. 9, 354–359.CrossRefGoogle Scholar
Nepomnyashchy, A. A. 1999 Solitons in viscous flows. In Fluid Dynamics at Interfaces (ed. Shyy, W. & Narayanan, R.), pp. 85–98. Cambridge University Press.Google Scholar
Peixinho, J., Mirbod, P. & Morris, J. F. 2012 Free surface flow between two horizontal concentric cylinders. Eur. Phys. J. E 35, 1–9.Google ScholarPubMed
Pozrikidis, C. 1998 Numerical studies of cusp formation at fluid interfaces in Stokes flow. J. Fluid Mech. 357, 29–57.CrossRefGoogle Scholar
Pudasaini, S. P. & Hutter, K. 2007 Dynamics of Rapid Flows of Dense Granular Avalanches. Springer.Google Scholar
Pumir, A., Manneville, P. & Pomeau, Y. 1983 On solitary waves running down an inclined plane. J. Fluid Mech. 135, 27–50.CrossRefGoogle Scholar
Saprykin, S., Demekhin, E. A. & Kalliadasis, S. 2005 Two-dimensional wave dynamics in thin films. I. Stationary solitary pulses. Phys. Fluids 15, 117105.Google Scholar
Scheid, B., Delacotte, J., Dollet, B., Rio, E., Restagno, F., van Nierop, E. A., Cantat, I., Langevin, D. & Stone, H. A. 2010 The role of surface rheology in liquid film formation. Europhys. Lett. 90, 24002.CrossRefGoogle Scholar
Scheid, B., Ruyer-Quil, C., Thiele, U., Kabov, O. A., Legros, J. C. & Colinet, P. 2005 Validity domain of the Benney equation including the Marangoni effect for closed and open flows. J. Fluid Mech. 527, 303–335.CrossRefGoogle Scholar
Thoroddsen, S. T. & Tan, Y. K. 2004 Free-surface entrainment into a rimming flow containing surfactants. Phys. Fluids 16, L13–L16.CrossRefGoogle Scholar