Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-23T14:28:16.586Z Has data issue: false hasContentIssue false
  • English
  • Français

An exact representation of the nonlinear triad interaction terms in spectral space

Published online by Cambridge University Press:  28 April 2014

Lawrence C. Cheung  and
Tamer A. Zaki
Lawrence C. Cheung*
Affiliation:
Department of Mechanical Engineering, Imperial College London, London SW7 2AZ, UK
Tamer A. Zaki*
Affiliation:
Department of Mechanical Engineering, Imperial College London, London SW7 2AZ, UK
*
‡Present address: GE Global Research, Niskayuna, NY 12309, USA.
†Present address: Johns Hopkins University, Baltimore, MD 21218, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

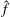Spectral analysis of the Navier–Stokes equations requires treatment of the convolution of pairs of Fourier transforms $\hat{f}$ and 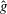$\hat{g}$. An exact, tractable representation of the nonlinear terms in spectral space is introduced, and relies on the definition and manipulation of a combination matrix. A spectral energy equation is derived where the nonlinear triad interactions are expressed using the combination matrix. The formulation is applied to the problem of homogeneous, isotropic turbulence. By finding the solution in an appropriate canonical basis, the energy spectrum in the inertial range 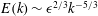$E(k)\sim \epsilon ^{2/3}k^{-5/3}$ is derived from the Navier–Stokes equations without invoking dimensional scaling arguments.

JFM classification

Turbulent Flows: Homogeneous turbulence Turbulent Flows: Isotropic turbulence Turbulent Flows: Turbulence theory
Type
Papers
Information
Journal of Fluid Mechanics , Volume 748 , 10 June 2014 , pp. 175 - 188
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Corrsin, S. 1951 On the spectrum of isotropic temperature fluctuations in isotropic turbulence. J. Appl. Phys. 22, 469–473.Google Scholar
Domaradzki, J. A. 1992 Nonlocal triad interactions and the dissipation range of isotropic turbulence. Phys. Fluids A 4 (9), 2037–2045.CrossRefGoogle Scholar
Domaradzki, J. A. & Rogallo, R. S. 1990 Local energy transfer and nonlocal interactions in homogeneous, isotropic turbulence. Phys. Fluids A 2, 413.Google Scholar
Durbin, P. A. & Reif, B. P. 2001 Statistical Theory and Modeling for Turbulent Flows. John Wiley & Sons.Google Scholar
Heisenberg, W. 1948 On the theory of statistical and isotropic turbulence. Proc. R. Soc. Lond. A 195 (1042), 402–406.Google Scholar
Kolmogorov, A. N. 1941a Dissipation of energy in the locally isotropic turbulence. Dokl. Akad. Nauk SSSR 32, 19–21.Google Scholar
Kolmogorov, A. N. 1941b The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Dokl. Akad. Nauk SSSR 30, 299–303.Google Scholar
Kraichnan, R. H. 1964 Kolmogorov’s hypotheses and Eulerian turbulence theory. Phys. Fluids 7 (11), 1723–1734.Google Scholar
Lesieur, M. 2008 Turbulence in Fluids. Springer.CrossRefGoogle Scholar
Lesieur, M., Montmory, C. & Chollet, J.-P. 1987 The decay of kinetic energy and temperature variance in three-dimensional isotropic turbulence. Phys. Fluids 30 (5), 1278–1286.Google Scholar
Métais, O. & Lesieur, M. 1992 Spectral large-eddy simulation of isotropic and stably stratified turbulence. J. Fluid Mech. 239 (1), 157–194.CrossRefGoogle Scholar
Ohkitani, K. & Kida, S. 1992 Triad interactions in a forced turbulence. Phys. Fluids A 4 (4), 794–802.CrossRefGoogle Scholar
Orszag, S. A. 1970 Analytical theories of turbulence. J. Fluid Mech. 41 (part 2), 363–386.Google Scholar
Praskovsky, A. A., Gledzer, E. B., Karyakin, M. Y. & Zhou, Y. 1993 The sweeping decorrelation hypothesis and energy-inertial scale interaction in high Reynolds number flows. J. Fluid Mech. 248, 493–511.Google Scholar
Sreenivasan, K. R. 1995 On the universality of the Kolmogorov constant. Phys. Fluids 7 (11), 2778–2784.Google Scholar
Sreenivasan, K. R. & Antonia, R. 1997 The phenomenology of small-scale turbulence. Annu. Rev. Fluid Mech. 29 (1), 435–472.Google Scholar
Tennekes, H. 1975 Eulerian and Lagrangian time microscales in isotropic turbulence. J. Fluid Mech. 67, 561–567.Google Scholar
Waleffe, F. 1992 The nature of triad interactions in homogeneous turbulence. Phys. Fluids A 4, 350.Google Scholar
Waleffe, F. 1993 Inertial transfers in the helical decomposition. Phys. Fluids A 5, 677.Google Scholar
Yeung, P., Brasseur, J. G. & Wang, Q. 1995 Dynamics of direct large-small scale couplings in coherently forced turbulence: concurrent physical-and Fourier-space views. J. Fluid Mech. 283, 43–96.Google Scholar
Yeung, P. K. & Zhou, Y. 1997 Universality of the Kolmogorov constant in numerical simulations of turbulence. Phys. Rev. 56 (2), 1746–1752.Google Scholar
Zhou, Y. 1993a Degrees of locality of energy transfer in the inertial range. Phys. Fluids A 5 (5), 1092–1094.Google Scholar
Zhou, Y. 1993b Interacting scales and energy transfer in isotropic turbulence. Phys. Fluids A 5 (10), 2511–2524.Google Scholar
Zhou, Y. 2010 Renormalization group theory for fluid and plasma turbulence. Phys. Rep. 488 (1), 1–49.Google Scholar
Zhou, Y., Matthaeus, W. H. & Dmitruk, P. 2004 Colloquium: magnetohydrodynamic turbulence and time scales in astrophysical and space plasmas. Rev. Mod. Phys. 76 (4), 1015–1035.Google Scholar
Zhou, Y., Praskovsky, A. A. & Vahala, G. 1993 A non-Gaussian phenomenological model for higher-order spectra in turbulence. Phys. Lett. A 178, 138–142.Google Scholar
Zhou, Y. & Rubinstein, R. 1996 Sweeping and straining effects in sound generation by high Reynolds number isotropic turbulence. Phys. Fluids 8 (3), 647–649.Google Scholar