Published online by Cambridge University Press: 15 December 2016
An entrainment model for lazy turbulent plumes is proposed, the resulting solutions of the plume conservation equations are developed and the implications for plume behaviour are considered and compared with the available experimental data. Indeed, the applicability of the classic solutions of the conservation equations subject to source conditions that produce lazy plumes, i.e. those with suitably high source Richardson number, contains an essential weakness: the underlying assumption of a constant entrainment coefficient. While entrainment models prescribing the dependence of the entrainment coefficient on the local Richardson number have been proposed for forced plumes, corresponding formulations for lazy plumes have not until now been considered. In the context of saline plumes, the model is applied directly. For hot gaseous plumes, we use a modified definition of buoyancy flux to recover a constant buoyancy flux in a non-stratified environment, despite the specific heat varying with the temperature. After a brief review of existing forced-plume formulations of entrainment, a power-law variation is adopted for the lazy plume. The plume equations are solved for the parameter 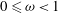 $0\leqslant \unicode[STIX]{x1D714}<1$, where
$0\leqslant \unicode[STIX]{x1D714}<1$, where  $\unicode[STIX]{x1D714}$ denotes the exponent of the power law. The cases of pure plumes and lazy plumes are then analysed in more detail; to the best of our knowledge this represents the first modelling of variable entrainment for lazy plumes. Specifically, it is shown that classic plume theory is recovered for
$\unicode[STIX]{x1D714}$ denotes the exponent of the power law. The cases of pure plumes and lazy plumes are then analysed in more detail; to the best of our knowledge this represents the first modelling of variable entrainment for lazy plumes. Specifically, it is shown that classic plume theory is recovered for 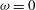 $\unicode[STIX]{x1D714}=0$, while for
$\unicode[STIX]{x1D714}=0$, while for 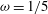 $\unicode[STIX]{x1D714}=1/5$ the plume equations may be solved using usual functions (notably polynomials) only. The results of the models for these cases are very similar, which advocates the idea of selecting systematically
$\unicode[STIX]{x1D714}=1/5$ the plume equations may be solved using usual functions (notably polynomials) only. The results of the models for these cases are very similar, which advocates the idea of selecting systematically 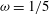 $\unicode[STIX]{x1D714}=1/5$, instead of
$\unicode[STIX]{x1D714}=1/5$, instead of 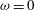 $\unicode[STIX]{x1D714}=0$, for cases where the effect of variation of entrainment is weak, since the new model leads to simple calculations. In the case of very lazy plumes, it is shown that, provided that a relevant value of
$\unicode[STIX]{x1D714}=0$, for cases where the effect of variation of entrainment is weak, since the new model leads to simple calculations. In the case of very lazy plumes, it is shown that, provided that a relevant value of 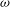 $\unicode[STIX]{x1D714}$ is chosen, the new model reproduces the available experimental results well.
$\unicode[STIX]{x1D714}$ is chosen, the new model reproduces the available experimental results well.