Hostname: page-component-669899f699-swprf Total loading time: 0 Render date: 2025-04-25T17:35:07.821Z Has data issue: false hasContentIssue false
  • English
  • Français

An atomistic model for the thermal resistance of a liquid–solid interface

Published online by Cambridge University Press:  11 January 2022

N.G. Hadjiconstantinou Open the ORCID record for N.G. Hadjiconstantinou [Opens in a new window]  and
M.M. Swisher Open the ORCID record for M.M. Swisher [Opens in a new window]
N.G. Hadjiconstantinou*
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
M.M. Swisher
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

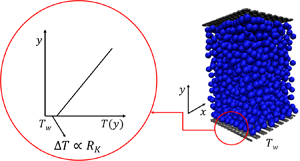
The thermal resistance associated with the interface between a solid and a liquid is analysed from an atomistic point of view. Partial evaluation of the associated Green–Kubo integral elucidates the various factors governing heat transport across the interface and leads to a quantitative model for the thermal resistance in terms of atomistic-level system parameters. The model is validated using molecular dynamics simulations.

JFM classification

Micro-/Nano-fluid dynamics: Microscale transport
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 934 , 10 March 2022 , R2
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

Alosious, S., Kannam, S.K., Sathian, S.P. & Todd, B.D. 2019 Prediction of Kapitza resistance at fluid–solid interfaces. J. Chem. Phys. 151, 194502.CrossRefGoogle ScholarPubMed
Alosious, S., Kannam, S.K., Sathian, S.P. & Todd, B.D. 2021 Nanoconfinement effects on the Kapitza resistance at water-CNT interfaces. Langmuir 37, 2355–2361.CrossRefGoogle ScholarPubMed
Barrat, J.-L. & Chiaruttini, F. 2003 Kapitza resistance at the liquid–solid interface. Mol. Phys. 101, 1605–1610.CrossRefGoogle Scholar
Bugel, M. & Galliero, G. 2008 Thermal conductivity of the Lennard-Jones fluid: an empirical correlation. Chem. Phys. 352, 249–257.CrossRefGoogle Scholar
Cahill, D.G., Ford, W.K., Goodson, K.E., Mahan, G.P., Majumdar, A., Maris, H.J., Merlin, R. & Phillpot, S.R. 2003 Nanoscale thermal transport. J. Appl. Phys. 93, 793–818.CrossRefGoogle Scholar
Egelstaff, P.A. 1994 An Introduction to the Liquid State. Clarendon Press.Google Scholar
Gordiz, K. & Henry, A. 2016 Phonon transport at crystalline Si/Ge interfaces: the role of interfacial modes of vibration. Sci. Rep. 6, 23139.CrossRefGoogle ScholarPubMed
Guo, Y., Surblys, D., Matsubara, H., Kawagoe, Y. & Ohara, T. 2020 Molecular dynamics study on the effect of long-chain surfactant adsorption on interfacial heat transfer between a polymer liquid and silica surface. J. Chem. Phys. C 124, 27558–27570.CrossRefGoogle Scholar
Hadjiconstantinou, N.G. 2006 The limits of Navier–Stokes theory and kinetic extensions for describing small-scale gaseous hydrodynamics. Phys. Fluids 18, 111301.CrossRefGoogle Scholar
Hadjiconstantinou, N.G. 2021 An atomistic model for the Navier slip condition. J. Fluid Mech. 912, A26.CrossRefGoogle Scholar
Hadjiconstantinou, N.G., Garcia, A.L., Bazant, M.Z. & He, G. 2003 Statistical error in particle simulations of hydrodynamic phenomena. J. Comp. Phys. 187, 274–297.CrossRefGoogle Scholar
Hansen, J.-P. & McDonald, I.R. 2013 Theory of Simple Liquids. Academic Press.Google Scholar
Heyes, D.M. 1988 Transport coefficients of Lennard-Jones fluids: a molecular dynamics and effective-hard-sphere treatment. Phys. Rev. B 37, 5677–5696.CrossRefGoogle ScholarPubMed
Heyes, D.M., Dini, D., Castigliola, L. & Dyre, J.C. 2019 Transport coefficients of the Lennard-Jones fluid close to the freezing line. J. Chem. Phys. 151, 204502.CrossRefGoogle Scholar
Hu, H. & Sun, Y. 2012 Effect of nanopatterns on Kapitza resistance at a water-gold interface during boiling: a molecular dynamics study. J. Appl. Phys. 112, 053508.CrossRefGoogle Scholar
Kavokine, N., Netz, R.R. & Bocquet, L. 2021 Fluids at the nanoscale: from continuum to subcontinuum transport. Annu. Rev. Fluid Mech. 53, 377–410.CrossRefGoogle Scholar
Kim, B.H., Beskok, A. & Kagin, T. 2008 Molecular dynamics simulations of thermal resistance at the liquid–solid interface. J. Chem. Phys. 129, 174701.CrossRefGoogle Scholar
Peraud, J.-P.M. & Hadjiconstantinou, N.G. 2016 Extending the range of validity of Fourier's law into the kinetic transport regime via asymptotic solution of the phonon Boltzmann transport equation. Phys. Rev. B 93, 045424.CrossRefGoogle Scholar
Plimpton, S. 1995 Fast parallel algorithms for short-range molecular dynamics. J. Comp. Phys. 117, 1–19.CrossRefGoogle Scholar
Ramos-Alvarado, B., Kumar, S. & Peterson, G.P. 2016 Solid–liquid thermal transport and its relationship with wettability and the interfacial liquid structure. J. Phys. Chem. Lett. 7, 3497–3501.CrossRefGoogle ScholarPubMed
Sone, Y. 2007 Molecular Gas Dynamics: Theory, Techniques, and Applications. Birkhauser.CrossRefGoogle Scholar
Song, G. & Min, C. 2013 Temperature dependence of thermal resistance at solid/liquid interface. Mol. Phys. 111, 903–908.CrossRefGoogle Scholar
Swartz, E.T. & Pohl, R.O. 1989 Thermal boundary resistance. Rev. Mod. Phys. 61, 605–668.CrossRefGoogle Scholar
Wang, G.J. & Hadjiconstantinou, N.G. 2017 Molecular mechanics and structure of the fluid–solid interface in simple fluids. Phys. Rev. Fluids 2, 094201.CrossRefGoogle Scholar
Wang, G.J. & Hadjiconstantinou, N.G. 2019 A universal molecular-kinetic scaling relation for slip of a simple fluid at a solid boundary. Phys. Rev. Fluids 4, 064291.CrossRefGoogle Scholar
Wang, Y. & Keblinski, P. 2011 Role of wetting and nanoscale roughness on thermal conductance at liquid–solid interface. Appl. Phys. Lett. 99, 073112.CrossRefGoogle Scholar
Zwanzig, R. & Mountain, R.D. 1965 High-frequency elastic moduli of simple fluids. J. Chem. Phys. 43, 4464–4471.CrossRefGoogle Scholar