Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-23T11:16:58.814Z Has data issue: false hasContentIssue false
  • English
  • Français

Amplitude modulation of streamwise velocity fluctuations in the roughness sublayer: evidence from large-eddy simulations

Published online by Cambridge University Press:  26 January 2016

William Anderson
William Anderson*
Affiliation:
Department of Mechanical Engineering, The University of Texas at Dallas, Richardson, TX, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Recent studies have demonstrated that large- and very-large-scale motions in the logarithmic region of turbulent boundary layers ‘amplitude modulate’ dynamics of the near-wall region (Marusic et al., Science, vol. 329, 2010, pp. 193–196; Mathis et al., J. Fluid Mech., vol. 628, 2009a, pp. 311–337). These contributions prompted development of a predictive model for near-wall dynamics (Mathis et al., J. Fluid Mech., vol. 681, 2011, pp. 537–566) that has promising implications for large-eddy simulations of wall turbulence at high Reynolds numbers (owing to the presence of smaller scales as the wall is approached). Existing studies on the existence of amplitude modulation in wall-bounded turbulence have addressed smooth-wall flows, though high Reynolds number rough-wall flows are ubiquitous. Under such conditions, the production of element-scale vortices ablates the viscous wall region and a new near-wall layer emerges: the roughness sublayer. 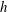The roughness sublayer depth scales with aggregate roughness element height, $h$, and is typically 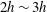$2h\sim 3h$. Above the roughness sublayer, Townsend’s hypothesis dictates that turbulence in the logarithmic layer is unaffected by the roughness sublayer (beyond its role in setting the friction velocity and thus inducing a deficit in the mean streamwise velocity known as the roughness function). Here, we present large-eddy simulation results of turbulent channel flow over rough walls. We follow the decoupling procedure outlined in Mathis et al. (J. Fluid Mech., vol. 628, 2009a, 311–337) and present evidence that outer-layer dynamics amplitude modulate the roughness sublayer. Below the roughness element height, we report enormous sensitivity to the streamwise–spanwise position at which flow statistics are measured, owing to spatial heterogeneities in the roughness sublayer imparted by roughness elements. For 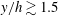$y/h\gtrsim 1.5$ (i.e. above the cubes, but within the roughness sublayer), topography dependence rapidly declines.

JFM classification

Geophysical and Geological Flows: Atmospheric flows Turbulent Flows: Turbulence modelling Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 789 , 25 February 2016 , pp. 567 - 588
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahn, J., Lee, J. H., Lee, J., Kang, J.-H. & Sung, H. J. 2015 Direct numerical simulation of a $30r$ long turbulent pipe flow at $Re_{{\it\tau}}=3008$ . Phys. Fluids 27, 065110.Google Scholar
Albertson, J. & Parlange, M. 1999 Surface length scales and shear stress: implications for land–atmosphere interaction over complex terrain. Water Resour. Res. 35, 2121–2132.Google Scholar
Anderson, W. 2012 An immersed boundary method wall model for high-Reynolds number channel flow over complex topography. Int. J. Numer. Methods Fluids 71, 1588–1608.CrossRefGoogle Scholar
Anderson, W. & Chamecki, M. 2014 Numerical study of turbulent flow over complex aeolian dune fields: the White Sands National Monument. Phys. Rev. E 89, 013005.Google ScholarPubMed
Anderson, W., Li, Q. & Bou-Zeid, E. 2015 Numerical simulation of flow over urban-like topographies and evaluation of turbulence temporal attributes. J. Turbulence 16, 809–831.CrossRefGoogle Scholar
Anderson, W. & Meneveau, C. 2010 A large-eddy simulation model for boundary-layer flow over surfaces with horizontally resolved but vertically unresolved roughness elements. Boundary-Layer Meteorol. 137, 397–415.Google Scholar
Anderson, W. & Meneveau, C. 2011 A dynamic large-eddy simulation model for boundary layer flow over multiscale, fractal-like surfaces. J. Fluid Mech. 679, 288–314.Google Scholar
Bai, K., Meneveau, C. & Katz, J. 2012 Near-wake turbulent flow structure and mixing length downstream of a fractal-tree. Boundary-Layer Meteorol. 143, 285–308.Google Scholar
Bailey, B. N. & Stoll, R. 2013 Turbulence in sparse, organized vegetative canopies: a large-eddy simulation study. Boundary-Layer Meteorol. 147, 369–400.Google Scholar
Balakumar, B. J. & Adrian, R. J. 2007 Large- and very-large-scale motions in channel and boundary-layer flows. Phil. Trans. R. Soc. Lond. A 365, 665–681.Google ScholarPubMed
Balaras, E. & Benocci, C.1994 Subgrid-scale models in finite-difference simulations of complex wall bounded flows. In AGARD CP 551. AGARD, Neuilly-sur-Seine, France, p. 2.15.Google Scholar
Balaras, E., Benocci, C. & Piomelli, U. 1996 Two layer approximate boundary conditions for large-eddy simulations. AIAA J. 34, 11119.Google Scholar
Bandyopadhyay, P. R. & Hussain, A. K. M. F. 1984 The coupling between scales in shear flows. Phys. Fluids 27, 2221–2228.Google Scholar
Belcher, S. E., Harman, I. N. & Finnigan, J. J. 2012 The wind in the willows: flows in forest canopies in complex terrain. Annu. Rev. Fluid Mech. 44, 479–504.Google Scholar
Bohm, M., Finnigan, J. J. & Raupach, M. R.2000 Dispersive fluxes and canopy flows: just how important are they? In Proc. 24th Conf. on Agricultural and Forest Meteorology. American Meteorological Society, Davis, CA, pp. 106–107.Google Scholar
Bons, J. P., Taylor, R. P., McClain, S. T. & Rivir, R. B. 2001 The many faces of turbine surface roughness. Trans. ASME J. Turbomach. 123, 739–748.CrossRefGoogle Scholar
Bou-Zeid, E., Meneveau, C. & Parlange, M. B. 2005 A scale-dependent Lagrangian dynamic model for large eddy simulation of complex turbulent flows. Phys. Fluids 17, 025105.Google Scholar
Calaf, M., Meneveau, C. & Meyers, J. 2010 Large eddy simulation study of fully developed wind-turbine array boundary layers. Phys. Fluids 22, 015110.Google Scholar
Calaf, M., Parlange, M. B. & Meneveau, C. 2011 Large eddy simulation study of scalar transport in fully developed wind-turbine array boundary layers. Phys. Fluids 23, 126603.CrossRefGoogle Scholar
Castro, I. P. 2007 Rough-wall boundary layers: mean flow universality. J. Fluid Mech. 585, 469–485.CrossRefGoogle Scholar
Chan, L., MacDonald, M., Chung, D., Hutchins, N. & Ooi, A. 2015 A systematic investigation of roughness height and wavelength in turbulent pipe flow in the transitionally rough regime. J. Fluid Mech. 771, 743–777.Google Scholar
Cheng, H. & Castro, I. P. 2002 Near wall flow over urban-like roughness. Boundary-Layer Meteorol. 104, 229–259.CrossRefGoogle Scholar
Chester, S., Meneveau, C. & Parlange, M. B. 2007 Modelling of turbulent flow over fractal trees with renormalized numerical simulation. J. Comput. Phys. 225, 427–448.Google Scholar
Coceal, O., Dobre, A., Thomas, T. G. & Belcher, S. E. 2007 Structure of turbulent flow over regular arrays of cubical roughness. J. Fluid Mech. 589, 375–409.Google Scholar
Deardorff, J. W. 1970 A numerical study of three-dimensional turbulent channel flow at large Reynolds numbers. J. Fluid Mech. 41, 453–480.Google Scholar
Deardorff, J. W. 1974 Three dimensional numerical study of turbulence in an entraining mixed layer. Boundary-Layer Meteorol. 7, 199–226.CrossRefGoogle Scholar
Dennis, D. J. C. & Nickels, T. B. 2011a Experimental measurement of large-scale three-dimensional structures in a turbulent boundary layer. Part 1. Vortex packets. J. Fluid Mech. 673, 180–217.CrossRefGoogle Scholar
Dennis, D. J. C. & Nickels, T. B. 2011b Experimental measurement of large-scale three-dimensional structures in a turbulent boundary layer. Part 2. Long structures. J. Fluid Mech. 673, 218–244.Google Scholar
Fang, J. & Porté-Agel, F. 2015 Large-eddy simulation of very-large-scale motions in the neutrally stratified atmospheric boundary layer. Boundary-Layer Meteorol. 155, 397–416.CrossRefGoogle Scholar
Finnigan, J. 2000 Turbulence in plant canopies. Annu. Rev. Fluid Mech. 32, 519–571.Google Scholar
Finnigan, J. J., Shaw, R. H. & Patton, E. G. 2009 Turbulence structure above a vegetation canopy. J. Fluid Mech. 637, 387–424.CrossRefGoogle Scholar
Flack, K. A. & Schultz, M. P. 2010 Review of hydraulic roughness scales in the fully rough regime. Trans. ASME J. Fluids Eng. 132, 041203.Google Scholar
Ganapathisubramani, B., Longmire, E. K. & Marusic, I. 2003 Characteristics of vortex packets in turbulent boundary layers. J. Fluid Mech. 478, 35–46.Google Scholar
Garratt, J. R. 1994 The Atmospheric Boundary Layer. Cambridge University Press.Google Scholar
Ghisalberti, M. 2009 Obstructed shear flows: similarities across systems and scales. J. Fluid Mech. 641, 51–61.Google Scholar
Graham, J. & Meneveau, C. 2012 Modeling turbulent flow over fractal trees using renormalized numerical simulation: alternate formulations and numerical experiments. Phys. Fluids 24, 125105.CrossRefGoogle Scholar
Grass, A. J. 1971 Structural features of turbulent flow over smooth and rough boundaries. J. Fluid Mech. 50, 233–255.CrossRefGoogle Scholar
Harmon, I. & Finnigan, J. J. 2007 A simple unified theory for flow in the canopy and roughness sublayer. Boundary-Layer Meteorol. 123, 339–364.Google Scholar
Hellström, L. H. O., Ganapathisubramania, B. & Smits, A. J. 2015 The evolution of large-scale motions in turbulent pipe flow. J. Fluid Mech. 779, 701–715.Google Scholar
Hong, J., Katz, J., Meneveau, C. & Schultz, M. 2012 Coherent structures and associated subgrid-scale energy transfer in a rough-wall channel flow. J. Fluid Mech. 712, 92–128.Google Scholar
Hong, J., Katz, J. & Schultz, M. 2011 Near-wall turbulence statistics and flow structures over three-dimensional roughness in a turbulent channel flow. J. Fluid Mech. 667, 1–37.CrossRefGoogle Scholar
Hutchins, N. & Marusic, I. 2007a Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Hutchins, N. & Marusic, I. 2007b Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. Lond. A 365, 647–664.Google ScholarPubMed
Hutchins, N., Nickels, T. B., Marusic, I. & Chong, M. S. 2009 Hot-wire spatial resolution issues in wall-bounded turbulence. J. Fluid Mech. 635, 103–136.CrossRefGoogle Scholar
Jimenez, J. 2004 Turbulent flow over rough wall. Annu. Rev. Fluid Mech. 36, 173–196.Google Scholar
Kim, K. C. & Adrian, R. J. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11, 417–422.Google Scholar
Krogstad, P.-A. & Antonia, R. A. 1994 Structure of turbulent boundary layers on smooth and rough walls. J. Fluid Mech. 277, 1–21.CrossRefGoogle Scholar
Leonardi, S. & Castro, I. P. 2010 Channel flow over large cube roughness: a direct numerical simulation study. J. Fluid Mech. 651, 519–539.CrossRefGoogle Scholar
Leonardi, S., Orlandi, P. & Antonia, R. A. 2007 Properties of $d$ - and $k$ -type roughness in a turbulent channel flow. Phys. Fluids 19, 125101.Google Scholar
Leonardi, S., Orlandi, P., Smalley, R. J., Djenidi, L. & Antonia, R. A. 2003 Direct numerical simulations of turbulent channel flow with transverse square bars on one wall. J. Fluid Mech. 491, 229–238.Google Scholar
Lundquist, K. A., Chow, F. K. & Lundquist, J. K. 2010 An immersed boundary method for the weather research and forecasting model. Mon. Weather Rev. 138, 796–817.Google Scholar
Marusic, I. & Heuer, W. D. C. 2007 Reynolds number invariance of the structure angle in wall turbulence. Phys. Rev. Lett. 99, 114501.Google Scholar
Marusic, I., Kunkel, G. J. & Porté-Agel, F. 2001 Experimental study of wall boundary conditions for large-eddy simulation. J. Fluid Mech. 446, 309–320.CrossRefGoogle Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2010 Predictive model for wall-bounded turbulent flow. Science 329, 193–196.CrossRefGoogle ScholarPubMed
Mason, P. J. 1994 Large-eddy simulation: a critical review of the technique. Q. J. R. Meteorol. Soc. 120, 1–26.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009a Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.CrossRefGoogle Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2011 A predictive inner–outer model for streamwise turbulence statistics in wall-bounded flows. J. Fluid Mech. 681, 537–566.Google Scholar
Mathis, R., Marusic, I., Chernyshenko, S. I. & Hutchins, N. 2013 Estimating wall-shear-stress fluctuations given an outer region input. J. Fluid Mech. 715, 163–180.CrossRefGoogle Scholar
Mathis, R., Monty, J. P., Hutchins, N. & Marusic, I. 2009b Comparison of large-scale amplitude modulation in turbulent boundary layers, pipes, and channel flows. Phys. Fluids 21, 111703.Google Scholar
Mejia-Alvarez, R. & Christensen, K. T. 2010 Low-order representations of irregular surface roughness and their impact on a turbulent boundary layer. Phys. Fluids 22, 015106.CrossRefGoogle Scholar
Meneveau, C. & Katz, J. 2000 Scale-invariance and turbulence models for large-eddy simulation. Annu. Rev. Fluid Mech. 32, 1–32.Google Scholar
Mittal, R. & Iaccarino, G. 2005 Immersed boundary methods. Annu. Rev. Fluid Mech. 37, 239–261.Google Scholar
Moeng, C.-H. 1984 A large-eddy-simulation model for the study of planetary boundary-layer turbulence. J. Atmos. Sci. 41, 2052–2062.Google Scholar
Nadeem, M., Lee, J. H., Lee, J. & Sung, H. J. 2015 Turbulent boundary layers over sparsely-spaced rod-roughened walls. Int. J. Heat Fluid Flow 56, 16–27.Google Scholar
Piomelli, U. 2008 Wall-layer models for large-eddy simulations. Prog. Aerosp. Sci. 44, 437–446.Google Scholar
Piomelli, U. & Balaras, E. 2002 Wall-layer models for large-eddy simulation. Annu. Rev. Fluid Mech. 34, 349–374.CrossRefGoogle Scholar
Piomelli, U., Ferziger, J., Moin, P. & Kim, J. 1989 New approximate boundary conditions for large eddy simulations of wall-bounded flows. Phys. Fluids A 1, 1061.Google Scholar
Pope, S. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Porté-Agel, F., Meneveau, C. & Parlange, M. B. 2000 A scale-dependent dynamic model for large-eddy simulation: application to a neutral atmospheric boundary layer. J. Fluid Mech. 415, 261–284.CrossRefGoogle Scholar
Rao, K. N., Narasimha, R. & Narayanan, M. A. B. 1971 The bursting phenomena in a turbulent boundary layer. J. Fluid Mech. 48, 339–352.Google Scholar
Raupach, M. R., Antonia, R. A. & Rajagopalan, S. 1991 Rough-wall turbulent boundary layers. Appl. Mech. Rev. 44, 1–25.CrossRefGoogle Scholar
Sagaut, P. 2002 Large Eddy Simulation for Incompressible Flows. Springer.Google Scholar
Schultz, M. P. 2007 Effects of coating roughness and biofouling on ship resistance and powering. Biofouling 23, 331–341.CrossRefGoogle ScholarPubMed
Scotti, A., Meneveau, C. & Lilly, D. K. 1993 Generalized Smagorinsky model for anisotropic grids. Phys. Fluids 5, 2306–2308.CrossRefGoogle Scholar
Smagorinsky, J. S. 1963 General circulation experiments with the primitive equations. Mon. Weather Rev. 91, 99–164.2.3.CO;2>CrossRefGoogle Scholar
Stevens, R. J. A. M., Wilczek, M. & Meneveau, C. 2014 Large-eddy simulation study of the logarithmic law for second- and higher-order moments in turbulent wall-bounded flow. J. Fluid Mech. 757, 888–907.Google Scholar
Talluru, K. M., Baidya, R., Hutchins, N. & Marusic, I. 2014 Amplitude modulation of all three velocity components in turbulent boundary layers. J. Fluid Mech. 746, R1,1–11.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Tseng, Y.-H., Meneveau, C. & Parlange, M. B. 2006 Modeling flow around bluff bodies and predicting urban dispersion using large-eddy simulation. Environ. Sci. Technol. 40, 2653–2662.CrossRefGoogle ScholarPubMed
Volino, R. J., Schultz, M. P. & Flack, K. A. 2007 Turbulence structure in rough- and smooth-wall boundary layers. J. Fluid Mech. 592, 263–293.Google Scholar
Wilczek, M., Stevens, R. J. A. M. & Meneveau, C. 2015 Spatio-temporal spectra in the logarithmic layer of wall turbulence: large-eddy simulations and simple models. J. Fluid Mech. 769, R1.Google Scholar
Wu, Y. & Christensen, K. T. 2007 Outer-layer similarity in the presence of a practical rough-wall topology. Phys. Fluids 19, 085108.CrossRefGoogle Scholar
Wu, Y. & Christensen, K. T. 2010 Spatial structure of a turbulent boundary layer with irregular surface roughness. J. Fluid Mech. 655, 380–418.CrossRefGoogle Scholar
Xie, Z.-T., Coceal, O. & Castro, I. P. 2008 Large-eddy simulation of flows over random urban-like obstacles. Boundary-Layer Meteorol. 129, 1–23.Google Scholar
Yang, X. I. A., Sadique, J., Mittal, R. & Meneveau, C. 2015 Integral wall model for large eddy simulations of wall-bounded turbulent flows. Phys. Fluids 27, 025112.CrossRefGoogle Scholar
Yuan, J. & Piomelli, U. 2014 Roughness effects on the Reynolds stress budgets in near-wall turbulence. J. Fluid Mech. 760, R1.CrossRefGoogle Scholar