Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-26T14:43:31.443Z Has data issue: false hasContentIssue false
  • English
  • Français

Amplification of random wave run-up on the front face of a box driven by tertiary wave interactions

Published online by Cambridge University Press:  02 May 2019

W. Zhao Open the ORCID record for W. Zhao [Opens in a new window] ,
P. H. Taylor ,
H. A. Wolgamot  and
R. Eatock Taylor
W. Zhao*
Affiliation:
Faculty of Engineering and Mathematical Sciences, The University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia
P. H. Taylor
Affiliation:
Faculty of Engineering and Mathematical Sciences, The University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia
H. A. Wolgamot
Affiliation:
Faculty of Engineering and Mathematical Sciences, The University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia
R. Eatock Taylor
Affiliation:
Department of Engineering Science, University of Oxford, OxfordOX1 3PJ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Wave run-up phenomena driven by nonlinear wave interactions with a fixed rectangular box are investigated. Experiments are carried out in different types of uni-directional waves with normal incidence. Significant wave run-ups featuring tertiary interaction effects, similar to those reported by Molin et al. (J. Fluid Mech., vol. 528, 2005, pp. 323–354) for a fixed vertical plate, are observed in regular wave tests. Transient wave group tests are conducted for comparison, to facilitate the analysis of the tertiary interactions in irregular waves. The most striking observation is that the wave surface elevations at the centre of the front face of the fixed box can reach 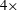$4\times$ the incident waves even in irregular waves, much larger than the 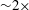${\sim}2\times$ predicted from linear theory and observed for the transient groups. The extra amplification builds up slowly and is localized on the weather side of the box. It is believed to result from tertiary interactions between the incident and reflected wave fields upstream, which induce a local lensing effect and thus wave focusing on the weather side. These interactions, though a nonlinear process, occur at the first harmonic quantities rather than high harmonics. Supporting evidence is extracted from random wave runs using NewWave analysis, where surface amplifications and phase lag – both key characteristics of tertiary wave interactions – are identified. The identification of these tertiary interactions in irregular waves is new, and may be of practical importance.

JFM classification

Waves/Free-surface Flows: Wave scattering
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 869 , 25 June 2019 , pp. 706 - 725
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bingham, H. B., Fuhrman, D. R., Jamois, E. & Kimmoun, O. 2004 Nonlinear wave interaction with bottom-mounted structures by a high-order Boussinesq method. In Proceedings of the 18th International Workshop on Water Waves and Floating Bodies, March 28–31, Cortona, Italy, http://www.iwwwfb.org/Abstracts/iwwwfb19/iwwwfb19_03.pdf.Google Scholar
Boccotti, P. 1983 Some new results on statistical properties of wind waves. Appl. Ocean Res. 5 (3), 134–140.Google Scholar
Faltinsen, O. M., Newman, J. N. & Vinje, T. 1995 Nonlinear wave loads on a slender vertical cylinder. J. Fluid Mech. 289, 179–198.Google Scholar
Fitzgerald, C. J., Taylor, P. H., Eatock Taylor, R., Grice, J. & Zang, J. 2014 Phase manipulation and the harmonic components of ringing forces on a surface-piercing column. Proc. R. Soc. Lond. A 470 (2168), 20130847.Google Scholar
Grice, J. R., Taylor, P. H. & Eatock Taylor, R. 2013 Near-trapping effects for multi-column structures in deterministic and random waves. Ocean Engng 58, 60–77.Google Scholar
Jamois, E., Fuhrman, D. R., Bingham, H. B. & Molin, B. 2006 A numerical study of nonlinear wave run-up on a vertical plate. Coast. Engng 53 (11), 929–945.Google Scholar
Jonathan, P. & Taylor, P. H. 1997 On irregular, nonlinear waves in a spread sea. J. Offshore Mech. Arctic Engng 119 (1), 37–41.Google Scholar
Lindgren, G. 1970 Some properties of a normal process near a local maximum. Ann. Math. Statist. 41, 1870–1883.Google Scholar
Longuet-Higgins, M. S. & Phillips, O. M. 1962 Phase velocity effects in tertiary wave interactions. J. Fluid Mech. 12 (3), 333–336.Google Scholar
Malenica, S. & Molin, B. 1995 Third-harmonic wave diffraction by a vertical cylinder. J. Fluid Mech. 302, 203–229.Google Scholar
Molin, B., Kimmoun, O., Liu, Y., Remy, F. & Bingham, H. B. 2010 Experimental and numerical study of the wave run-up along a vertical plate. J. Fluid Mech. 654, 363–386.Google Scholar
Molin, B., Kimmoun, O., Remy, F. & Chatjigeorgiou, I. K. 2014 Third-order effects in wave–body interaction. Eur. J. Mech. (B/Fluids) 47, 132–144.Google Scholar
Molin, B., Remy, F. & Kimmoun, O. 2007 Second-order wave interaction with a vertical plate. J. Engng Maths 58 (1–4), 109–119.Google Scholar
Molin, B., Remy, F., Kimmoun, O. & Ferrant, P. 2003 Third-order interactions and wave run-up. In Proceedings of the 18th International Workshop on Water Waves and Floating Bodies, April 6–9, Le Croisic, France, http://www.iwwwfb.org/Abstracts/iwwwfb18/iwwwfb18_36.pdf.Google Scholar
Molin, B., Remy, F., Kimmoun, O. & Jamois, E. 2005 The role of tertiary wave interactions in wave-body problems. J. Fluid Mech. 528, 323–354.Google Scholar
Ohl, C. O. G., Eatock Taylor, R., Taylor, P. H. & Borthwick, A. G. L. 2001 Water wave diffraction by a cylinder array. Part 1. Regular waves. J. Fluid Mech. 442, 1–32.Google Scholar
Phillips, O. M. 1981 Wave interactions – the evolution of an idea. J. Fluid Mech. 106, 215–227.Google Scholar
Santo, H., Taylor, P. H., Moreno, E. C., Stansby, P., Eatock Taylor, R., Sun, L. & Zang, J. 2017 Extreme motion and response statistics for survival of the three-float wave energy converter M4 in intermediate water depth. J. Fluid Mech. 813, 175–204.Google Scholar
Sun, L., Eatock Taylor, R. & Taylor, P. H. 2015 Wave driven free surface motion in the gap between a tanker and an FLNG barge. Appl. Ocean Res. 51, 331–349.Google Scholar
Zhao, W., Taylor, P. H., Wolgamot, H. A. & Eatock Taylor, R. 2018a Identifying linear and nonlinear coupling between fluid sloshing in tanks, roll of a barge and external free-surface waves. J. Fluid Mech. 844, 403–434.Google Scholar
Zhao, W., Taylor, P. H., Wolgamot, H. A. & Eatock Taylor, R. 2018b Linear viscous damping in random wave excited gap resonance at laboratory scale – NewWave analysis and reciprocity. J. Fluids Struct. 80, 59–76.Google Scholar
Zhao, W., Wolgamot, H. A., Taylor, P. H. & Eatock Taylor, R. 2017 Gap resonance and higher harmonics driven by focused transient wave groups. J. Fluid Mech. 812, 905–939.Google Scholar