Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-22T22:25:53.779Z Has data issue: false hasContentIssue false
  • English
  • Français

Air entrainment in dynamic wetting: Knudsen effects and the influence of ambient air pressure

Published online by Cambridge University Press:  25 March 2015

James E. Sprittles Open the ORCID record for James E. Sprittles [Opens in a new window]
James E. Sprittles*
Affiliation:
Mathematics Institute, University of Warwick, Coventry CV4 7AL, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

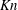Recent experiments on coating flows and liquid drop impact both demonstrate that wetting failures caused by air entrainment can be suppressed by reducing the ambient gas pressure. Here, it is shown that non-equilibrium effects in the gas can account for this behaviour, with ambient pressure reductions increasing the mean free path of the gas and hence the Knudsen number $\mathit{Kn}$. These effects first manifest themselves through Maxwell slip at the boundaries of the gas, so that for sufficiently small 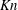$\mathit{Kn}$ they can be incorporated into a continuum model for dynamic wetting flows. The resulting mathematical model contains flow structures on the nano-, micro- and millimetre scales and is implemented into a computational platform developed specifically for such multiscale phenomena. The coating flow geometry is used to show that for a fixed gas–liquid–solid system (a) the increased Maxwell slip at reduced pressures can substantially delay air entrainment, i.e. increase the ‘maximum speed of wetting’, (b) unbounded maximum speeds are obtained, as the pressure is reduced only when slip at the gas–liquid interface is allowed for, and (c) the observed behaviour can be rationalised by studying the dynamics of the gas film in front of the moving contact line. A direct comparison with experimental results obtained from a dip-coating process shows that the model recovers most trends but does not accurately predict some of the high viscosity data at reduced pressures. This discrepancy occurs because the gas flow enters the ‘transition regime’, so that more complex descriptions of its non-equilibrium nature are required. Finally, by collapsing onto a master curve experimental data obtained for drop impact in a reduced pressure gas, it is shown that the same physical mechanisms are also likely to govern splash suppression phenomena.

JFM classification

Materials Processing Flows: Coating Interfacial Flows (free surface): Contact lines Rarefied Gas Flow: Rarefied Gas Flow
Type
Papers
Information
Journal of Fluid Mechanics , Volume 769 , 25 April 2015 , pp. 444 - 481
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agarwal, A. & Prabhu, S. V. 2008 Survey on measurement of tangential momentum accommodation coefficient. J. Vac. Sci. Technol. A 26, 634–645.Google Scholar
Allen, M. D. & Raabe, O. G. 1982 Re-evaluation of Millikan’s oil drop data for the motion of small particles in air. J. Aerosol Sci. 6, 537–547.CrossRefGoogle Scholar
Andrews, M. K. & Harris, P. D. 1995 Damping and gas viscosity measurements using a microstructure. Sensors Actuators A 49, 103–108.CrossRefGoogle Scholar
Benkreira, H. & Ikin, J. B. 2010 Dynamic wetting and gas viscosity effects. Chem. Engng Sci. 65, 1790–1796.CrossRefGoogle Scholar
Benkreira, H. & Khan, M. I. 2008 Air entrainment in dip coating under reduced air pressures. Chem. Engng Sci. 63, 448–459.CrossRefGoogle Scholar
Bird, G. A. 1994 Molecular Gas Dynamics and the Direct Simulation of Gas Flows. Clarendon.CrossRefGoogle Scholar
Blake, T. D. 2006 The physics of moving wetting lines. J. Colloid Interface Sci. 299, 1–13.Google Scholar
Blake, T. D., Clarke, A. & Ruschak, K. J. 1994 Hydrodynamic assist of wetting. AIChE J. 40, 229–242.Google Scholar
Blake, T. D. & De Coninck, J. 2002 The influence of solid–liquid interactions on dynamic wetting. Adv. Colloid Interface Sci. 96, 21–36.CrossRefGoogle ScholarPubMed
Blake, T. D., Dobson, R. A. & Ruschak, K. J. 2004 Wetting at high capillary numbers. J. Colloid Interface Sci. 279, 198–205.CrossRefGoogle ScholarPubMed
Blake, T. D. & Haynes, J. M. 1969 Kinetics of liquid/liquid displacement. J. Colloid Interface Sci. 30, 421–423.Google Scholar
Blake, T. D. & Ruschak, K. J. 1979 A maximum speed of wetting. Nature 282, 489–491.Google Scholar
Blake, T. D. & Shikhmurzaev, Y. D. 2002 Dynamic wetting by liquids of different viscosity. J. Colloid Interface Sci. 253, 196–202.CrossRefGoogle ScholarPubMed
Bouwhuis, W., van der Veen, R. C. A., Tran, T., Keij, D. L., Winkels, K. G., Peters, I. R., van der Meer, D., Sun, C., Snoeijer, J. H. & Lohse, D. 2012 Maximal air bubble entrainment at liquid-drop impact. Phys. Rev. Lett. 109, 264501.CrossRefGoogle ScholarPubMed
Burley, R. & Kennedy, B. S. 1976 An experimental study of air entrainment at a solid/liquid/gas interface. Chem. Engng Sci. 31, 901–911.CrossRefGoogle Scholar
Bussmann, M., Chandra, S. & Mostaghimi, J. 2000 Modeling the splash of a droplet impacting a solid surface. Phys. Fluids 12, 3121–3132.Google Scholar
Cercignani, C. 2000 Rarefied Gas Dynamics: From Basic Concepts to Actual Calculations. Cambridge University Press.Google Scholar
Chan, T. S., Srivastava, S., Marchand, A., Andreotti, B., Biferale, L., Toschi, F. & Snoeijer, J. H. 2013 Hydrodynamics of air entrainment by moving contact lines. Phys. Fluids 25, 074105.CrossRefGoogle Scholar
Chapman, S. & Cowling, T. G. 1970 The Mathematical Theory of Non-Uniform Gases: An Account of the Kinetic Theory of Viscosity, Thermal conduction and Diffusion in Gases. Cambridge University Press.Google Scholar
Clarke, A. 2002 Coating on a rough surface. AIChE J. 48, 2149–2156.Google Scholar
Clarke, A. & Stattersfield, E. 2006 Direct evidence supporting nonlocal hydrodynamic influence on the dynamic contact angle. Phys. Fluids 18, 048106.Google Scholar
Cox, R. G. 1986 The dynamics of the spreading of liquids on a solid surface. Part 1. Viscous flow. J. Colloid Interface Sci. 168, 169–194.Google Scholar
De Coninck, J. & Blake, T. D. 2008 Wetting and molecular dynamics simulations of simple fluids. Annu. Rev. Mater. Res. 38, 1–22.Google Scholar
Dejaguin, B. V. & Levi, S. M. 1964 Film Coating Theory. Focal.Google Scholar
Derby, B. 2010 Inkjet printing of functional and structural materials: fluid property requirements, feature stability and resolution. Annu. Rev. Mater. Res. 40, 395–414.Google Scholar
Driscoll, M. M. & Nagel, S. R. 2011 Ultrafast interference imaging of air in splashing dynamics. Phys. Rev. Lett. 107, 154502.Google Scholar
Duchemin, L. & Josserand, C. 2012 Rarefied gas correction for the bubble entrapment singularity in drop impacts. C. R. Méc. 340, 797–803.Google Scholar
Duez, C., Ybert, C., Clanet, C. & Bocquet, L. 2007 Making a splash with water repellency. Nat. Phys. 3, 180–183.Google Scholar
Dussan, E. B. V. 1976 The moving contact line: the slip boundary condition. J. Fluid Mech. 77, 665–684.Google Scholar
Dussan, E. B. V. 1977 Immiscible liquid displacement in a capillary tube: the moving contact line. AIChE J. 23, 131–133.Google Scholar
Dussan, E. B. V. & Davis, S. H. 1974 On the motion of a fluid–fluid interface along a solid surface. J. Fluid Mech. 65, 71–95.CrossRefGoogle Scholar
Dussan, E. B. V., Ramé, E. & Garoff, S. 1991 On identifying the appropriate boundary conditions at a moving contact line: an experimental investigation. J. Fluid Mech. 230, 97–116.Google Scholar
Eggers, J. 2004 Hydrodynamic theory of forced dewetting. Phys. Rev. Lett. 93, 094502.Google Scholar
Eggers, J., Fontelos, M. A., Josserand, C. & Zaleski, S. 2010 Drop dynamics after impact on a solid wall: theory and simulations. Phys. Fluids 22, 062101.CrossRefGoogle Scholar
Gad-el-Hak, M.(Ed.) 2006 Flow physics. In MEMS: Introduction and Fundamentals, 4-1–36, CRC.Google Scholar
Hadjiconstantinou, N. G. 2003 Comment on Cercignani’s second-order slip coefficient. Phys. Fluids 15, 2352–2354.CrossRefGoogle Scholar
Hocking, L. M. 1976 A moving fluid interface on a rough surface. J. Fluid Mech. 76, 801–807.Google Scholar
Hoffman, R. L. 1975 A study of the advancing interface. I. Interface shape in liquid–gas systems. J. Colloid Interface Sci. 50, 228–241.Google Scholar
Huh, C. & Mason, S. G. 1977 The steady movement of a liquid meniscus in a capillary tube. J. Fluid Mech. 81, 401–409.Google Scholar
Huh, C. & Scriven, L. E. 1971 Hydrodynamic model of steady movement of a solid/liquid/fluid contact line. J. Colloid Interface Sci. 35, 85–101.Google Scholar
Jacqmin, D. 2002 Very, very fast wetting. J. Fluid Mech. 455, 347–358.Google Scholar
Kistler, S. F. 1993 Hydrodynamics of wetting. In Wettability (ed. Berg, J. C.), pp. 311–429. Marcel Dekker.Google Scholar
Kistler, S. F. & Scriven, L. E. 1983 Coating flows. In Computational Analysis of Polymer Processing (ed. Pearson, J. R. A. & Richardson, S. M.), pp. 243–299. Applied Science Publishers.Google Scholar
Kolinski, J. M., Mahadevan, L. & Rubinstein, S. M. 2014 Drops can bounce from perfectly hydrophilic surfaces. Europhys. Lett. 108, 24001.Google Scholar
Kolinski, J. M., Rubinstein, S. M., Mandre, S., Brenner, M. P., Weitz, D. A. & Mahadevan, L. 2012 Skating on a film of air: drops impacting on a surface. Phys. Rev. Lett. 108, 074503.Google Scholar
Koplik, J. & Banavar, J. R. 1995 Continuum deductions from molecular hydrodynamics. Annu. Rev. Fluid Mech. 27, 257–292.Google Scholar
Lauga, E., Brenner, M. & Stone, H. A. 2007 Microfluidics: the no-slip boundary condition. In Springer Handbook of Experimental Fluid Mechanics, pp. 1219–1240. Springer.Google Scholar
Liu, Y., Tan, P. & Xu, L. 2015 Kelvin–Helmholtz instability in an ultrathin air film causes drop splashing on smooth surfaces. Proceedings of the National Academy of Sciences.Google Scholar
Lockerby, D. A., Reese, J. M., Emerson, D. R. & Barber, R. W. 2004 Velocity boundary condition at solid walls in rarefied gas calculations. Phys. Rev. E 70, 017303.Google Scholar
Lockerby, D. A., Reese, J. M. & Gallis, M. A. 2005a Capturing the Knudsen layer in continuum-fluid models of nonequilibrium gas flows. AIAA J. 43, 1391–1393.Google Scholar
Lockerby, D. A., Reese, J. M. & Gallis, M. A. 2005b The usefulness of higher-order constitutive relations for describing the Knudsen layer. Phys. Fluids 17, 100609.Google Scholar
Mandre, S. & Brenner, M. P. 2012 The mechanism of a splash on a dry solid surface. J. Fluid Mech. 690, 148–172.Google Scholar
Mani, M., Mandre, S. & Brenner, M. P. 2010 Events before droplet splashing on a solid surface. J. Fluid Mech. 647, 163–185.Google Scholar
Marchand, A., Chan, T. S., Snoeijer, J. H. & Andreotti, B. 2012 Air entrainment by contact lines of a solid plate plunged into a viscous fluid. Phys. Rev. Lett. 108, 204501.Google Scholar
Maxwell, J. C. 1867 On the dynamical theory of gases. Phil. Trans. R. Soc. Lond. 157, 49–88.Google Scholar
Maxwell, J. C. 1879 On stresses in rarified gases arising from inequalities of temperature. Phil. Trans. R. Soc. Lond. 170, 231–256.Google Scholar
Millikan, R. A. 1923 The general law of fall of a small spherical body through a gas, and its bearing upon the nature of molecular reflection from surfaces. Phys. Rev. 22, 1–23.Google Scholar
Mues, W., Hens, J. & Boiy, L. 1989 Observation of a dynamic wetting process using laser-Doppler velocimetry. AIChE J. 35, 1521–1526.Google Scholar
Navier, C. L. M. H. 1823 Mémoire sur les lois mouvement des fluides. Mém. Présentés par Divers Savants Acad. Sci. Inst. Fr. 6, 389–440.Google Scholar
Ngan, C. G. & Dussan, E. B. V. 1982 On the nature of the dynamic contact angle: an experimental study. J. Fluid Mech. 118, 27–40.Google Scholar
Ramé, E. & Garoff, S. 1996 Microscopic and macroscopic dynamic interface shapes and the interpretation of dynamic contact angles. J. Colloid Interface Sci. 177, 234–244.CrossRefGoogle ScholarPubMed
Rein, M. 1993 Phenomena of liquid drop impact on solid and liquid surfaces. Fluid Dyn. Res. 12, 61–93.Google Scholar
Rein, M. & Delplanque, J.-P. 2008 The role of air entrainment on the outcome of drop impact on a solid surface. Acta Mechanica 201, 105–118.Google Scholar
Riboux, G. & Gordillo, J. M. 2014 Experiments of drops impacting a smooth solid surface: a model of the critical impact speed for drop splashing. Phys. Rev. Lett. 113, 024507.Google Scholar
de Ruiter, J., Lagraauw, R., Ende, D. & Mugele, F. 2015 Wettability-independent bouncing on flat surfaces mediated by thin air films. Nat. Phys. 11, 48–53.Google Scholar
de Ruiter, J., Oh, J. M., Ende, D. & Mugele, F. 2012 Dynamics of collapse of air films in drop impact. Phys. Rev. Lett. 108, 074505.Google Scholar
Ruschak, K. J. 1980 A method for incorporating free boundaries with surface tension in finite element fluid-flow simulators. Intl J. Numer. Meth. Engng 15, 639–648.Google Scholar
Schroll, R. D., Josserand, C., Zaleski, S. & Zhang, W. W. 2010 Impact of a viscous liquid drop. Phys. Rev. Lett. 104, 034504.Google Scholar
Shikhmurzaev, Y. D. 1997 Moving contact lines in liquid/liquid/solid systems. J. Fluid Mech. 334, 211–249.Google Scholar
Shikhmurzaev, Y. D. 2006 Singularities at the moving contact line. Mathematical, physical and computational aspects. Physica D 217, 121–133.CrossRefGoogle Scholar
Shikhmurzaev, Y. D. 2007 Capillary Flows with Forming Interfaces. Chapman & Hall/CRC.CrossRefGoogle Scholar
Simmons, J. A., Sprittles, J. E. & Shikhmurzaev, Y. D. 2015 The formation of a bubble from a submerged orifice. Eur. J. Mech. (B/Fluids). (in press).Google Scholar
Simpkins, P. G. & Kuck, V. J. 2003 On air entrainment in coatings. J. Colloid Interface Sci. 263, 562–571.Google Scholar
Smith, F. T., Li, L. & Wu, G. X. 2003 Air cushioning with a lubrication/inviscid balance. J. Fluid Mech. 482, 291–318.Google Scholar
Snoeijer, J. H. & Andreotti, B. 2013 Moving contact lines: scales, regimes, and dynamical transitions. Annu. Rev. Fluid Mech. 45, 269–292.CrossRefGoogle Scholar
Snoeijer, J. H., Andreotti, B., Delon, G. & Fermigier, M. 2007 Relaxation of a dewetting contact line. Part 1. A full-scale hydrodynamic calculation. J. Fluid Mech. 579, 63–83.Google Scholar
Snoeijer, J. H., Delon, G., Fermigier, M. & Andreotti, B. 2006 Avoided critical behavior in dynamically forced wetting. Phys. Rev. Lett. 96, 174504.Google Scholar
Sprittles, J. E. & Shikhmurzaev, Y. D. 2012a Coalescence of liquid drops: different models versus experiment. Phys. Fluids 24, 122105.Google Scholar
Sprittles, J. E. & Shikhmurzaev, Y. D. 2012b The dynamics of liquid drops and their interaction with solids of varying wettabilities. Phys. Fluids 24, 082001.Google Scholar
Sprittles, J. E. & Shikhmurzaev, Y. D. 2012c A finite element framework for describing dynamic wetting phenomena. Intl J. Numer. Meth. Fluids 68, 1257–1298.Google Scholar
Sprittles, J. E. & Shikhmurzaev, Y. D. 2013 Finite element simulation of dynamic wetting flows as an interface formation process. J. Comput. Phys. 233, 34–65.Google Scholar
Sprittles, J. E. & Shikhmurzaev, Y. D. 2014a Dynamics of liquid drops coalescing in the inertial regime. Phys. Rev. E 89, 063006.Google Scholar
Sprittles, J. E. & Shikhmurzaev, Y. D. 2014b A parametric study of the coalescence of liquid drops in a viscous gas. J. Fluid Mech. 753, 279–306.Google Scholar
Sundararajakumar, R. R. & Koch, D. L. 1996 Non-continuum lubrication flows between particles colliding in a gas. J. Fluid Mech. 313, 283–308.Google Scholar
Tanner, L. H. 1979 The spreading of silicone drops on horizontal surfaces. J. Phys. D: Appl. Phys. 12, 1473–1484.Google Scholar
Thoroddsen, S. T., Etoh, T. G. & Takehara, K. 2005 The air bubble entrapped under a drop impacting on a solid surface. J. Fluid Mech. 545, 203–212.Google Scholar
Vandre, E., Carvalho, M. S. & Kumar, S. 2012 Delaying the onset of dynamic wetting failure through meniscus confinement. J. Fluid Mech. 707, 496–520.CrossRefGoogle Scholar
Vandre, E., Carvalho, M. S. & Kumar, S. 2013 On the mechanism of wetting failure during fluid displacement along a moving substrate. Phys. Fluids 25, 102103.Google Scholar
Vandre, E., Carvalho, M. S. & Kumar, S. 2014 Characteristics of air entrainment during dynamic wetting failure along a planar substrate. J. Fluid Mech. 747, 119–140.Google Scholar
Velarde, M. G. 2011 Discussion and debate: wetting and spreading science – quo vadis? In The European Physical Journal Special Topics (ed. Velarde, M. G.), vol. 197. Springer.Google Scholar
Voinov, O. V. 1976 Hydrodynamics of wetting. Fluid Dyn. 11, 714–721.Google Scholar
Weinstein, S. J. & Ruschak, K. J. 2004 Coating flows. Annu. Rev. Fluid Mech. 36, 29–53.Google Scholar
Wilson, M. C. T., Summers, J. L., Shikhmurzaev, Y. D., Clarke, A. & Blake, T. D. 2006 Nonlocal hydrodynamic influence on the dynamic contact angle: slip models versus experiment. Phys. Rev. E 83, 041606.Google Scholar
Xu, L. 2007 Liquid drop splashing on smooth, rough, and textured surfaces. Phys. Rev. E 75, 056316.Google Scholar
Xu, L., Zhang, W. & Nagel, S. R. 2005 Drop splashing on a dry smooth surface. Phys. Rev. Lett. 94, 184505.Google Scholar
Yarin, A. L. 2006 Drop impact dynamics: splashing, spreading, receding, bouncing. Annu. Rev. Fluid Mech. 38, 159–192.Google Scholar