Article contents
Air entrainment and bubble statistics in breaking waves
Published online by Cambridge University Press: 19 July 2016
Abstract
We investigate air entrainment and bubble statistics in three-dimensional breaking waves through novel direct numerical simulations of the two-phase air–water flow, resolving the length scales relevant for the bubble formation problem, the capillary length and the Hinze scale. The dissipation due to breaking is found to be in good agreement with previous experimental observations and inertial scaling arguments. The air entrainment properties and bubble size statistics are investigated for various initial characteristic wave slopes. For radii larger than the Hinze scale, the bubble size distribution, can be described by 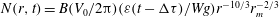 $N(r,t)=B(V_{0}/2{\rm\pi})({\it\varepsilon}(t-{\rm\Delta}{\it\tau})/Wg)r^{-10/3}r_{m}^{-2/3}$ during the active breaking stages, where
$N(r,t)=B(V_{0}/2{\rm\pi})({\it\varepsilon}(t-{\rm\Delta}{\it\tau})/Wg)r^{-10/3}r_{m}^{-2/3}$ during the active breaking stages, where 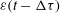 ${\it\varepsilon}(t-{\rm\Delta}{\it\tau})$ is the time-dependent turbulent dissipation rate, with
${\it\varepsilon}(t-{\rm\Delta}{\it\tau})$ is the time-dependent turbulent dissipation rate, with 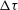 ${\rm\Delta}{\it\tau}$ the collapse time of the initial air pocket entrained by the breaking wave,
${\rm\Delta}{\it\tau}$ the collapse time of the initial air pocket entrained by the breaking wave, 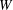 $W$ a weighted vertical velocity of the bubble plume,
$W$ a weighted vertical velocity of the bubble plume, 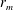 $r_{m}$ the maximum bubble radius,
$r_{m}$ the maximum bubble radius, 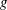 $g$ gravity,
$g$ gravity, 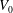 $V_{0}$ the initial volume of air entrained,
$V_{0}$ the initial volume of air entrained,  $r$ the bubble radius and
$r$ the bubble radius and 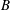 $B$ a dimensionless constant. The active breaking time-averaged bubble size distribution is described by
$B$ a dimensionless constant. The active breaking time-averaged bubble size distribution is described by 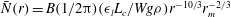 $\bar{N}(r)=B(1/2{\rm\pi})({\it\epsilon}_{l}L_{c}/Wg{\it\rho})r^{-10/3}r_{m}^{-2/3}$, where
$\bar{N}(r)=B(1/2{\rm\pi})({\it\epsilon}_{l}L_{c}/Wg{\it\rho})r^{-10/3}r_{m}^{-2/3}$, where 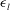 ${\it\epsilon}_{l}$ is the wave dissipation rate per unit length of breaking crest,
${\it\epsilon}_{l}$ is the wave dissipation rate per unit length of breaking crest, 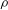 ${\it\rho}$ the water density and
${\it\rho}$ the water density and 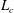 $L_{c}$ the length of breaking crest. Finally, the averaged total volume of entrained air,
$L_{c}$ the length of breaking crest. Finally, the averaged total volume of entrained air, 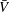 $\bar{V}$, per breaking event can be simply related to
$\bar{V}$, per breaking event can be simply related to 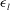 ${\it\epsilon}_{l}$ by
${\it\epsilon}_{l}$ by 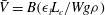 $\bar{V}=B({\it\epsilon}_{l}L_{c}/Wg{\it\rho})$, which leads to a relationship for a characteristic slope,
$\bar{V}=B({\it\epsilon}_{l}L_{c}/Wg{\it\rho})$, which leads to a relationship for a characteristic slope, 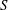 $S$, of
$S$, of 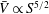 $\bar{V}\propto S^{5/2}$. We propose a phenomenological turbulent bubble break-up model based on earlier models and the balance between mechanical dissipation and work done against buoyancy forces. The model is consistent with the numerical results and existing experimental results.
$\bar{V}\propto S^{5/2}$. We propose a phenomenological turbulent bubble break-up model based on earlier models and the balance between mechanical dissipation and work done against buoyancy forces. The model is consistent with the numerical results and existing experimental results.
JFM classification
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 187
- Cited by



