Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-01-09T21:42:21.586Z Has data issue: false hasContentIssue false
  • English
  • Français

Air cushioning and bubble entrapment in three-dimensional droplet impacts

Published online by Cambridge University Press:  13 April 2010

PETER D. HICKS  and
RICHARD PURVIS
PETER D. HICKS*
Affiliation:
School of Mathematics, University of East Anglia, Norwich NR4 7TJ, UK
RICHARD PURVIS
Affiliation:
School of Mathematics, University of East Anglia, Norwich NR4 7TJ, UK
*
†Present address: Department of Mathematics, University College London, Gower Street, London WC1E 6BT, UK. Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Droplet deformation by air cushioning prior to impact is considered. A model is presented coupling the free-surface deformation of a droplet with the pressure field in the narrow air layer generated as a droplet approaches an impact. The model is based upon the density and viscosity in the air being small compared with those in the liquid. 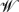Additionally, the Reynolds number, defined using the droplet radius ℛ and approach velocity l, is such that lubrication forces dominate in the air layer. In the absence of significant surface tension or compressibility effects, these assumptions lead to coupled nonlinear integro-differential equations describing the evolution of a droplet free surface approaching a solid wall through air, with or without topography.

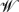The problem is studied numerically with a boundary-element method in the inviscid droplet coupled with a finite-difference method in the lubricating air. In normal impacts, air cushioning will be shown to deflect the free surface upwards, delaying the moment of touchdown and trapping a bubble. The volume of the bubble is found to be (μg4/3ℛ5/3/ρl4/3l4/3)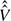, where μg is the gas viscosity and ρl is the liquid density and the numerically computed pre-factor 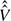= 94.48. Bubble volumes predicted by this relationship are shown to be in good agreement with experimental observations. In oblique impact or impact with a moving surface with sufficient horizontal motion a bubble is not trapped beneath the approaching droplet. In this case, the region of touchdown is initially crescent shaped with air effects accelerating the moment of touchdown.

Type
Papers
Information
Journal of Fluid Mechanics , Volume 649 , 25 April 2010 , pp. 135 - 163
Copyright
Copyright © Cambridge University Press 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Chandra, S. & Avedisian, C. T. 1991 On the collision of a droplet with a solid surface. Proc. R. Soc. Lond. A 432, 13.Google Scholar
van Dam, D. B. & Le Clerc, C. 2004 Experimental study of the impact of an ink-jet printed droplet on a solid substrate. Phys. Fluids 16 (9), 3403–3414.CrossRefGoogle Scholar
Dell'Aversana, P., Tontodonato, V. & Carotenuto, L. 1997 Suppression of coalescence and of wetting: the shape of the interstitial film. Phys. Fluids 9 (9), 2475–2485.CrossRefGoogle Scholar
Gopinath, A. & Koch, D. L. 2002 Collision and rebound of small droplets in an incompressible continuum gas. J. Fluid Mech. 454, 145–201.CrossRefGoogle Scholar
Gueyffier, D., Li, J., Nadim, A., Scardovelli, R. & Zaleski, S. 1999 Approximate factorization for time-dependent partial differential equations. J. Comput. Phys. 152, 423–456.CrossRefGoogle Scholar
Howison, S. D., Ockendon, J. R. & Oliver, J. M. 2002 Deep- and shallow-water slamming at small and zero deadrise angles. J. Engng Math. 42, 373–388.CrossRefGoogle Scholar
Howison, S. D., Ockendon, J. R., Oliver, J. M., Purvis, R. & Smith, F. T. 2005 Droplet impact on a thin fluid layer. J. Fluid Mech. 542, 1–23.CrossRefGoogle Scholar
Howison, S. D., Ockendon, J. R. & Wilson, S. K. 1991 Incompressible water-entry problems at small deadrise angles. J. Fluid Mech. 222, 215–230.CrossRefGoogle Scholar
Iafrati, A. 2007 Air–water interaction in breaking waves. In Proceedings of the International Conference on Violent Flows (ed. Kashiwagi, M.), vol. VF-2007, pp. 83–93.Google Scholar
Josserand, C. & Zaleski, S. 2003 Droplet splashing on a thin liquid film. Phys. Fluids 15 (6), 1650–1657.CrossRefGoogle Scholar
King, A. C. & Tuck, E. O. 1993 Thin fluid layers supported by surface traction. J. Fluid Mech. 251, 709–718.CrossRefGoogle Scholar
King, A. C., Tuck, E. O. & Vanden-Broeck, J. M. 1993 Air-blown waves on thin viscous sheets. Phys. Fluids A 5, 973–978.CrossRefGoogle Scholar
Korobkin, A. A. 1997 Asymptotic theory of liquid–solid impact. Phil. Trans. R. Soc. Lond. A 355, 507–522.CrossRefGoogle Scholar
Korobkin, A. A. 1999 Shallow water impact problems. J. Engng Math. 35, 233–250.CrossRefGoogle Scholar
Korobkin, A. A., Ellis, A. S. & Smith, F. T. 2008 Trapping of air in impact between a body and shallow water. J. Fluid Mech. 611, 365–394.CrossRefGoogle Scholar
Lesser, M. B. & Field, J. E. 1983 The impact of compressible liquids. Annu. Rev. Fluid Mech. 15, 97–122.CrossRefGoogle Scholar
Liow, J. L. 2001 Splash formation by spherical drops. J. Fluid Mech. 427, 73–105.Google Scholar
Mandre, S., Mani, M. & Brenner, M. P. 2009 Precursors to splashing of liquid droplets on a solid surface. Phys. Rev. Lett. 102 (13), 134502.CrossRefGoogle ScholarPubMed
Mehdi-Nejad, V., Mostaghimi, J. & Chandra, S. 2003 Air bubble entrapment under an impacting droplet. Phys. Fluids 15, 173–183.CrossRefGoogle Scholar
Miozzi, M., Lugni, C., Brocchini, M. & Faltinsen, O. M. 2007 The role of the air-entrapment in the flip-through evolution. In Proceedings of the International Conference on Violent Flows, vol. VF-2007, pp. 327–335.Google Scholar
Neitzel, G. P. & Dell'Aversana, P. 2002 Noncoalescence and nonwetting behaviour of liquids. Annu. Rev. Fluid Mech. 34, 267–289.CrossRefGoogle Scholar
Nethercote, W. C. E., Mackay, M. & Menon, B. 1986 Some warship slamming investigations. Tech Memo 86/206. DREA.Google Scholar
Oliver, J. M. 2002 Water entry and related problems. PhD thesis, University of Oxford.Google Scholar
Oliver, J. M. 2007 Second-order wagner theory for two-dimensional water-entry problems at small deadrise angles. J. Fluid Mech. 572, 59–85.CrossRefGoogle Scholar
Prosperetti, A. & Oguz, H. N. 1993 The impact of drops on liquid surfaces and the underwater noise of rain. Annu. Rev. Fluid Mech. 25, 577–602.CrossRefGoogle Scholar
Protière, S., Boudaoud, A. & Couder, Y. 2006 Particle–wave association on a fluid interface. J. Fluid Mech. 554, 85–108.CrossRefGoogle Scholar
Purvis, R. & Smith, F. T. 2004 a Air–water interactions near droplet impact. Eur. J. Appl. Math. 15, 853–871.CrossRefGoogle Scholar
Purvis, R. & Smith, F. T. 2004 b Large droplet impact on water layers. Paper 2004–0414. AIAA. In 42nd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV.CrossRefGoogle Scholar
Smith, F. T., Li, L. & Wu, G. X. 2003 Air cushioning with a lubrication/inviscid balance. J. Fluid Mech. 482, 291–318.CrossRefGoogle Scholar
Smith, F. T., Ovenden, N. C. & Purvis, R. 2006 Industrial and biomedical applications. In One Hundred Years of Boundary Layer Research (ed. Meier, G. E. A., Sreenivasan, K. R. & Heinemann, H.-J.) pp. 291–300, Proceedings of IUTAM Symposium, Kluwer Academic.CrossRefGoogle Scholar
Smith, F. T. & Purvis, R. 2005 Air effects on droplet impact. Paper 2005-5184. AIAA. In 4th AIAA Theoretical Fluid Mechanics Meeting, Toronto, ON, Canada.Google Scholar
Smith, M. K. & Neitzel, G. P. 2006 Multiscale modelling in the numerical computation of isothermal non-wetting. J. Fluid Mech. 554, 67–83.CrossRefGoogle Scholar
Thoroddsen, S. T., Etoh, T. G. & Takehara, K. 2003 Air entrapment under an impacting drop. J. Fluid Mech. 478, 125–134.CrossRefGoogle Scholar
Thoroddsen, S. T., Etoh, T. G., Takehara, K., Ootsuka, N. & Hatsuki, Y. 2005 The air bubble entrapped under a drop impacting on a solid surface. J. Fluid Mech. 545, 203–212.CrossRefGoogle Scholar
Vanden-Broeck, J.-M. 2001 Damped waves generated by a moving pressure distribution. Eur. J. Appl. Maths. 12, 387–400.Google Scholar
Vanden-Broeck, J.-M. & Smith, F. T. 2008 Surface tension effects on interaction between two fluids near a wall. Quart. J. Mech. Appl. Math. 61 (2), 117–128.CrossRefGoogle Scholar
Ward, S. N. 2001 Landslide tsunami. J. Geophys. Res. 100, 24487–24498.Google Scholar
Ward, S. N. & Day, S. 2001 Cumbre Vieja Volcano – potential collapse and tsunami at La Palma, Canary Islands. Geophys. Res. Lett. 28 (17), 3397–3400.CrossRefGoogle Scholar
Wilson, S. K. 1991 A mathematical model for the initial stages of fluid impact in the presence of a cushioning fluid layer. J. Engng Math. 25 (3), 265–285.CrossRefGoogle Scholar