Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-01-09T21:46:40.946Z Has data issue: false hasContentIssue false
  • English
  • Français

Aero-optics of subsonic turbulent boundary layers

Published online by Cambridge University Press:  24 February 2012

Kan Wang  and
Meng Wang
Kan Wang
Affiliation:
Institute for Flow Physics and Control, Department of Aerospace and Mechanical Engineering, University of Notre Dame, Notre Dame, IN 46556, USA
Meng Wang*
Affiliation:
Institute for Flow Physics and Control, Department of Aerospace and Mechanical Engineering, University of Notre Dame, Notre Dame, IN 46556, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

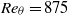Compressible large-eddy simulations are carried out to study the aero-optical distortions caused by Mach 0.5 flat-plate turbulent boundary layers at Reynolds numbers of , 1770 and 3550, based on momentum thickness. The fluctuations of refractive index are calculated from the density field, and wavefront distortions of an optical beam traversing the boundary layer are computed based on geometric optics. The effects of aperture size, small-scale turbulence, different flow regions and beam elevation angle are examined and the underlying flow physics is analysed. It is found that the level of optical distortion decreases with increasing Reynolds number within the Reynolds-number range considered. The contributions from the viscous sublayer and buffer layer are small, while the wake region plays a dominant role, followed by the logarithmic layer. By low-pass filtering the fluctuating density field, it is shown that small-scale turbulence is optically inactive. Consistent with previous experimental findings, the distortion magnitude is dependent on the propagation direction due to anisotropy of the boundary-layer vortical structures. Density correlations and length scales are analysed to understand the elevation-angle dependence and its relation to turbulence structures. The applicability of Sutton’s linking equation to boundary-layer flows is examined, and excellent agreement between linking equation predictions and directly integrated distortions is obtained when the density length scale is appropriately defined.

JFM classification

Boundary Layers: Boundary Layers Compressible Flows: Compressible Flows Turbulent Flows: Turbulence simulation
Type
Papers
Information
Journal of Fluid Mechanics , Volume 696 , 10 April 2012 , pp. 122 - 151
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Adrian, R. J. 2007 Haripin vortex organization in wall turbulence. Phys. Fluids 19, 1–16.CrossRefGoogle Scholar
2. Bodony, D. 2006 Analysis of sponge zones for computational fluid mechanics. J. Comput. Phys. 212, 681–702.CrossRefGoogle Scholar
3. Buckner, A., Gordeyev, S. & Jumper, E. J. 2005 Optical aberrations caused by transonic attached boundary layers: underlying flow structure. AIAA Paper 2005–0752.CrossRefGoogle Scholar
4. Cassady, P. E., Birch, S. F. & Terry, P. J. 1989 Aero-optical analysis of compressible flow over an open cavity. AIAA J. 27, 758–762.Google Scholar
5. Choi, H. & Moin, P. 1990 On the space–time characteristics of wall-pressure fluctuations. Phys. Fluids A 2, 1450–1460.CrossRefGoogle Scholar
6. Cress, J. 2010 Optical aberrations caused by coherent structures in a subsonic, compressible, turbulent boundary layer. PhD thesis, University of Notre Dame.Google Scholar
7. Cress, J., Gordeyev, S. & Jumper, E. J. 2010 Aero-optical measurements in a heated, subsonic, turbulent boundary layer. AIAA Paper 2010–0434.Google Scholar
8. Cress, J., Gordeyev, S., Post, M. & Jumper, E. J. 2008 Aero-optical measurements in a turbulent, subsonic boundary layer at different elevation angles. AIAA Paper 2008–4214.Google Scholar
9. DeGraaff, D. & Eaton, J. 2000 Reynolds-number scaling of the flat-plate turbulent boundary layer. J. Fluid Mech. 422, 319–346.CrossRefGoogle Scholar
10. Fitzgerald, E. J. & Jumper, E. J. 2004 The optical distortion mechanism in a nearly incompressible free shear layer. J. Fluid Mech. 512, 153–189.CrossRefGoogle Scholar
11. Garnier, E., Adams, N. & Sagaut, P. 2009 Large Eddy Simulation for Compressible Flows. Springer.Google Scholar
12. Geary, J. M. 1995 Introduction to Wavefront Sensors. SPIE Press.Google Scholar
13. Gilbert, K. G. & Otten, L. J.  (Eds) 1982 Aero-Optical Phenomena, Progress in Astronautics and Aeronautics. AIAA.Google Scholar
14. Gladstone, J. H. & Dale, T. P. 1863 Researches on the refraction, dispersion, and sensitivities of liquids. Phil. Trans. R. Soc. Lond. 153, 317–343.Google Scholar
15. Gordeyev, S. & Jumper, E. J. 2010 Fluid dynamics and aero-optics of turrets. Prog. Aerosp. Sci. 46, 388–400.CrossRefGoogle Scholar
16. Gordeyev, S., Jumper, E. J. & Hayden, T. 2011 Aero-optics of supersonic boundary layers. AIAA Paper 2011–1325.CrossRefGoogle Scholar
17. Gordeyev, S., Jumper, E. J., Ng, T. T. & Cain, A. B. 2003 Aero-optical characteristics of compressible subsonic turbulent boundary layer. AIAA Paper 2003–3606.Google Scholar
18. Havener, G. 1992 Optical wave front variance: a study on analytic models in use today. AIAA Paper 92–0654.CrossRefGoogle Scholar
19. Hugo, R. J. & Jumper, E. J. 2000 Applicability of the aero-optic linking equation to a high coherent, transitional shear layer. Appl. Opt. 39, 4392–4401.CrossRefGoogle Scholar
20. Israeli, M. & Orszag, S. 1981 Approximation of radiation boundary conditions. J. Comput. Phys. 41, 115–135.Google Scholar
21. Jumper, E. J. & Fitzgerald, E. J. 2001 Recent advances in aero-optics. Prog. Aerosp. Sci. 37, 299–339.CrossRefGoogle Scholar
22. Liepmann, H. W. 1952 Deflection and diffusion of a light ray passing through a boundary layer. Tech. Rep. SM-14397. Douglas Aircraft Company, Santa Monica Division, Santa Monica, CA.Google Scholar
23. Lilly, D. K. 1992 A proposed modification of the Germano subgrid-scale closure method. Phys. Fluids 4, 633–635.CrossRefGoogle Scholar
24. Lund, T. S., Wu, X. & Squires, K. 1998 Generation of turbulent inflow data for spatially-developing boundary layer simulations. J. Comput. Phys. 140, 233–258.CrossRefGoogle Scholar
25. Mahajan, V. N. 1983 Strehl ratio for primary aberrations in terms of their aberration variance. J. Opt. Soc. Am. 73, 860–861.CrossRefGoogle Scholar
26. Malley, M. M., Sutton, G. W. & Kincheloe, N. 1992 Beam-jitter measurements of turbulent aero-optical path differences. Appl. Opt. 31, 4440–4443.CrossRefGoogle ScholarPubMed
27. Mani, A., Moin, P. & Wang, M. 2009 Computational study of optical distortions by separated shear layers and turbulent wakes. J. Fluid Mech. 625, 273–298.CrossRefGoogle Scholar
28. Mani, A., Wang, M. & Moin, P. 2006 Statistical description of free-space propagation for highly aberrated optical beams. J. Opt. Soc. Am. A 23, 3027–3035.Google Scholar
29. Mani, A., Wang, M. & Moin, P. 2008 Resolutions requirements for aero-optical simulations. J. Comput. Phys. 227, 9008–9020.Google Scholar
30. Moin, P., Squires, K., Cabot, W. & Lee, S. 1991 A dynamic subgrid-scale model for compressible turbulence and scalar transport. Phys. Fluids 11, 2746–2757.Google Scholar
31. Monin, A. S. & Yaglom, A. M. 1975 Statistical Fluid Mechanics: Mechanics of Turbulence, vol. II. MIT.Google Scholar
32. Robinson, S. K. 1991 Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech. 23, 601–639.Google Scholar
33. Shoeybi, M., Svard, M., Ham, F. E. & Moin, P. 2010 An adaptive implicit-explicit scheme for the DNS and LES of compressible flows on unstructured grids. J. Comput. Phys. 229, 5944–5965.Google Scholar
34. Steinmetz, W. J. 1982 Second moments of optical degradation due to a thin turbulent layer. In Aero-Optical Phenomena (ed. Gilbert, K. G. & Otten, L. J. ), Progress in Astronautics and Aeronautics , vol. 80, pp. 78–100. AIAA.Google Scholar
35. Sutton, G. W. 1985 Aero-optical foundations and applications. AIAA J. 23, 1525–1537.CrossRefGoogle Scholar
36. Tromeur, E., Garnier, E. & Sagaut, P. 2006a Analysis of the Sutton model for aero-optical properties of compressible boundary layers. J. Fluids Engng-Trans. ASME 128, 239–246.CrossRefGoogle Scholar
37. Tromeur, E., Garnier, E. & Sagaut, P. 2006b Large-eddy simulation of aero-optical effects in a spatially developing turbulent boundary layer. J. Turbul. 7, 1–28.CrossRefGoogle Scholar
38. Tromeur, E., Garnier, E., Sagaut, P. & Basdevant, C. 2003 Large eddy simulation of aero-optical effects in a turbulent boundary layer. J. Turbul. 4, 1–22.CrossRefGoogle Scholar
39. Truman, C. R. 1992 The influence of turbulent structure on optical phase distortion through turbulent shear flows. AIAA Paper 92–2817.Google Scholar
40. Truman, C. R. & Lee, M. J. 1990 Effects of organized turbulence structures on the phase distortion in a coherent optical beam propagation through a turbulence shear flow. Phys. Fluids 2, 851–857.CrossRefGoogle Scholar
41. Tsai, Y. P. & Christiansen, W. H. 1990 Two-dimensional numerical simulation of shear-layer optics. AIAA J. 28, 2092–2097.CrossRefGoogle Scholar
42. Tyson, R. K. 1997 Principles of Adaptive Optics, 2nd edn. Academic.Google Scholar
43. Urbin, G. & Knight, D. 2001 Large-eddy simulation of a supersonic boundary layer using an unstructured grid. AIAA J. 39, 1288–1295.Google Scholar
44. Wang, M., Mani, A. & Gordeyev, S. 2012 Physics and computation of aero-optics. Annu. Rev. Fluid Mech. 44, 299–321.CrossRefGoogle Scholar
45. Wittich, D., Gordeyev, S. & Jumper, E. J. 2007 Revised scaling of optical distortions caused by compressible, subsonic turbulent boundary layers. AIAA Paper 2007-4009.Google Scholar
46. Wyckham, C. M. & Smits, A. 2009 Aero-optic distortion in transonic and hypersonic turbulent boundary layers. AIAA J. 47, 2158–2168.CrossRefGoogle Scholar
47. Zubair, F. R. & Catrakis, H. J. 2007 Aero-optical resolution robustness in turbulent separated shear layers at large Reynolds numbers. AIAA J. 45, 2721–2728.CrossRefGoogle Scholar