Published online by Cambridge University Press: 01 December 2011
It is known experimentally that an aerofoil immersed in a uniform stream at a moderate Reynolds number emits tones. However, there have been major differences in the experimental observations in the past. Some experiments reported the observation of multiple tones, with strong evidence that these tones are most probably generated by a feedback loop. There is also an experiment reporting the observation of a single tone with no tonal jump or other features associated with feedback. In spite of the obvious differences in the experimental observations published in the literature, it is noted that all the dominant tone frequencies measured in all the investigations are in agreement with an empirically derived Paterson formula. The objective of the present study is to perform a direct numerical simulation (DNS) of the flow and acoustic phenomenon to investigate the tone generation mechanism. When comparing with experimental studies, numerical simulations appear to have two important advantages. The first is that there is no background wind tunnel noise in numerical simulation. This avoids the signal-to-noise ratio problem inherent in wind tunnel experiments. In other words, it is possible to study tones emitted by a truly isolated aerofoil computationally. The second advantage is that DNS produces a full set of space–time data, which can be very useful in determining the tone generation processes. The present effort concentrates on the tones emitted by three NACA0012 aerofoils with a slightly rounded trailing edge but with different trailing edge thickness at zero degree angle of attack. At zero degree angle of attack, in the Reynolds number range of 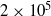 to
to 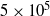 , the boundary layer flow is attached nearly all the way to the trailing edge of the aerofoil. Unlike an aerofoil at an angle of attack, there is no separation bubble, no open flow separation. All the flow separation features tend to increase the complexity of the tone generation processes. The present goal is limited to finding the basic tone generation mechanism in the simplest flow configuration. Our DNS results show that, for the flow configuration under study, the aerofoil emits only a single tone. This is true for all three aerofoils over the entire Reynolds number range of the present study. In the literature, it is known that Kelvin–Helmholtz instabilities of free shear layers generally have a much higher spatial growth rate than that of the Tollmien–Schlichting boundary layer instabilities. A near-wake non-parallel flow instability analysis is performed. It is found that the tone frequencies are the same as the most amplified Kelvin–Helmholtz instability at the location where the wake has a minimum half-width. This suggests that near-wake instability is the energy source of aerofoil tones. However, flow instabilities at low subsonic Mach numbers generally do not cause strong tones. An investigation of how near-wake instability generates tones is carried out using the space–time data provided by numerical simulations. Our observations indicate that the dominant tone generation process is the interaction of the oscillatory motion of the near wake, driven by flow instability, with the trailing edge of the aerofoil. Secondary mechanisms involving unsteady near-wake motion and the formation of discrete vortices in regions further downstream are also observed.
, the boundary layer flow is attached nearly all the way to the trailing edge of the aerofoil. Unlike an aerofoil at an angle of attack, there is no separation bubble, no open flow separation. All the flow separation features tend to increase the complexity of the tone generation processes. The present goal is limited to finding the basic tone generation mechanism in the simplest flow configuration. Our DNS results show that, for the flow configuration under study, the aerofoil emits only a single tone. This is true for all three aerofoils over the entire Reynolds number range of the present study. In the literature, it is known that Kelvin–Helmholtz instabilities of free shear layers generally have a much higher spatial growth rate than that of the Tollmien–Schlichting boundary layer instabilities. A near-wake non-parallel flow instability analysis is performed. It is found that the tone frequencies are the same as the most amplified Kelvin–Helmholtz instability at the location where the wake has a minimum half-width. This suggests that near-wake instability is the energy source of aerofoil tones. However, flow instabilities at low subsonic Mach numbers generally do not cause strong tones. An investigation of how near-wake instability generates tones is carried out using the space–time data provided by numerical simulations. Our observations indicate that the dominant tone generation process is the interaction of the oscillatory motion of the near wake, driven by flow instability, with the trailing edge of the aerofoil. Secondary mechanisms involving unsteady near-wake motion and the formation of discrete vortices in regions further downstream are also observed.