Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-05T04:47:01.690Z Has data issue: false hasContentIssue false
  • English
  • Français

Advection and buoyancy-induced turbulent mixing in a narrow vertical tank

Published online by Cambridge University Press:  29 April 2013

Daan D. J. A. van Sommeren ,
C. P. Caulfield  and
Andrew W. Woods
Daan D. J. A. van Sommeren
Affiliation:
BP Institute, University of Cambridge, Madingley Road, Cambridge CB3 0EZ, UK Department of Applied Mathematics and Theoretical Physics, Wilberforce Road, Cambridge CB3 0WA, UK
C. P. Caulfield*
Affiliation:
BP Institute, University of Cambridge, Madingley Road, Cambridge CB3 0EZ, UK Department of Applied Mathematics and Theoretical Physics, Wilberforce Road, Cambridge CB3 0WA, UK
Andrew W. Woods
Affiliation:
BP Institute, University of Cambridge, Madingley Road, Cambridge CB3 0EZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We describe new experiments to examine the buoyancy-induced turbulent mixing which results from the injection of a small constant volume flux of dense fluid at the top of a long narrow vertical tank with square cross-section, in which a steady laminar upward flow of less dense fluid is present. To conserve volume of fluid in the tank, fluid leaves the tank through two small openings near the top of the tank. Dense source fluid vigorously mixes with the less dense fluid of the upward flow, such that a dense mixing region of turbulent fluid propagates downwards during the transient mixing phase of the experiment. Eventually, the transport of dense fluid associated with the buoyancy-induced turbulent flow is balanced by the transport of less-dense fluid associated with the steady upward flow, such that the mixing region evolves into a layer of finite extent which stays approximately constant in height during a statistically steady mixing phase of the experiment. With an ideal source of downward constant buoyancy flux 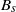${B}_{s} $ at the top of the tank, tank width 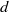$d$, and speed of the upward flow 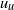${u}_{u} $, we perform experiments with Froude numbers 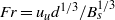$\mathit{Fr}= {u}_{u} {d}^{1/ 3} / { B}_{s}^{1/ 3} $ ranging between 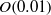$O(0. 01)$ and 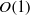$O(1)$. The steady-state height of the mixing region and the maximum reduced gravity as found near the source of buoyancy flux at the top of the tank increase with decreasing Froude number. For the experiments with intermediate values of the Froude number, we find that the steady-state mixing region is small enough to be contained in the experimental tank, but large enough not to be dominated by developing turbulence near the source of buoyancy flux. For these experiments, we show that the key buoyancy-induced turbulent mixing properties are not significantly affected by the upward flow. We use a dye-attenuation technique to obtain vertical profiles of the time- and horizontally averaged reduced gravity to show a good agreement between the experimental profiles and the solution of a nonlinear turbulent advection–diffusion equation during the steady mixing phase. Furthermore, we discuss the characteristic time scale of the transient mixing phase. We compare our experimental results with the numerical solution of a time-dependent nonlinear turbulent advection–diffusion equation during the transient mixing phase. We also describe three reduced models for the evolution of the reduced gravity distribution in the mixing region, and we demonstrate these models’ usefulness by comparison with our experimental results and the numerical solution of the time-dependent nonlinear turbulent advection–diffusion equation.

JFM classification

Turbulent Flows: Turbulent Flows Mixing: Turbulent mixing
Type
Papers
Information
Journal of Fluid Mechanics , Volume 724 , 10 June 2013 , pp. 450 - 479
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baird, M. H. I., Aravamudan, K., Rao, N. V. Rama, Chadam, J. & Peirce, A. P. 1992 Unsteady axial mixing by natural convection in a vertical column. AIChE J. 38, 1825–1834.Google Scholar
Barnett, S. 1991 The dynamics of buoyant releases in confined spaces. PhD thesis, DAMTP University of Cambridge.Google Scholar
Dalziel, S. B., Patterson, M. D., Caulfield, C. P. & Coomaraswamy, I. A. 2008 Mixing efficiency in high-aspect-ratio Rayleigh–Taylor experiments. Phys. Fluids 20, 065106.CrossRefGoogle Scholar
Debacq, M., Fanguet, V., Hulin, J. P., Salin, D. & Perrin, B. 2001 Self-similar concentration profiles in buoyant mixing of miscible fluids in a vertical tube. Phys. Fluids 13, 3097–3100.CrossRefGoogle Scholar
Hardcastle, S. & McKinnon, D. L. 2010 Mine ventilation: proceedings of the 13th U.S./North American Mine Ventilation Symposium. Sudbury, Ontario, Canada: MIRARCO.Google Scholar
Holmes, T. L., Karr, A. E. & Baird, M. H. I. 1991 Effect of unfavourable continuous phase density gradient on axial mixing. AIChE J. 37, 360–366.CrossRefGoogle Scholar
Karmis, M. 2001 Mine Health and Safety Management. SME.Google Scholar
Kucuker, H. 2006 Occupational fatalities among coal mine workers in zonguldak, Turkey, 1994–2003. Occup. Med. 56, 144–150.Google Scholar
Prandtl, L. 1925 A report on testing for built-up turbulence. Z. Angew. Math. Mech. 5, 136–139.CrossRefGoogle Scholar
Pratt, H. R. C. & Baird, M. H. I. 1983 Axial dispersion. In Handbook of Solvent Extraction (ed. Lo, T. C., Baird, M. H. I. & Hanson, C.), chap. 5, pp. 199–247. Wiley-Interscience.Google Scholar
Séon, T., Hulin, J.-P., Salin, D., Perrin, B. & Hinch, E. J. 2004 Buoyant mixing of miscible fluids in tilted tubes. Phys. Fluids 16, L103–L106.Google Scholar
Séon, T., Znaien, J., Perrin, B., Hinch, E. J., Salin, D. & Hulin, J. P. 2007 Front dynamics and macroscopic diffusion in buoyant mixing in a tilted tube. Phys. Fluids 19, 123603.CrossRefGoogle Scholar
van Sommeren, D. D. J. A. 2013 The dynamics of buoyancy induced mixing in a narrow vertical tank. PhD thesis, DAMTP/BPI University of Cambridge.Google Scholar
van Sommeren, D. D. J. A., Caulfield, C. P. & Woods, A. W. 2012 Turbulent buoyant convection from a maintained source of buoyancy in a narrow vertical tank. J. Fluid Mech. 701, 278–303.CrossRefGoogle Scholar
Taylor, G. I. 1954 The dispersion of matter in turbulent flow through a pipe. Proc. R. Soc. Lond. A 223, 446–468.Google Scholar
Terazawa, K., Takatori, T., Tomii, S. & Nakano, K. 1985 Methane asphyxia. coal mine accident investigation of distribution of gas. Am. J. Forensic Med. Pathol. 6, 211–215.Google Scholar
Zukoski, E. E. 1995 Review of flows driven by natural convection in adiabatic shafts. Tech Rep. NIST-GCR-95-679. U.S. Department of Commerce, National Institute of Standard and Technology, Building and Fire Research Laboratory.Google Scholar