Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T06:53:03.117Z Has data issue: false hasContentIssue false
  • English
  • Français

Adjoint-based parametric sensitivity analysis for swirling M-flames

Published online by Cambridge University Press:  21 November 2018

Calum S. Skene  and
Peter J. Schmid Open the ORCID record for Peter J. Schmid [Opens in a new window]
Calum S. Skene*
Affiliation:
Department of Mathematics, Imperial College London, London SW7 2AZ, UK
Peter J. Schmid
Affiliation:
Department of Mathematics, Imperial College London, London SW7 2AZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A linear numerical study is conducted to quantify the effect of swirl on the response behaviour of premixed lean flames to general harmonic excitation in the inlet, upstream of combustion. This study considers axisymmetric M-flames and is based on the linearised compressible Navier–Stokes equations augmented by a simple one-step irreversible chemical reaction. Optimal frequency response gains for both axisymmetric and non-axisymmetric perturbations are computed via a direct–adjoint methodology and singular value decompositions. The high-dimensional parameter space, containing perturbation and base-flow parameters, is explored by taking advantage of generic sensitivity information gained from the adjoint solutions. This information is then tailored to specific parametric sensitivities by first-order perturbation expansions of the singular triplets about the respective parameters. Valuable flow information, at a negligible computational cost, is gained by simple weighted scalar products between direct and adjoint solutions. We find that for non-swirling flows, a mode with azimuthal wavenumber $m=2$ is the most efficiently driven structure. The structural mechanism underlying the optimal gains is shown to be the Orr mechanism for 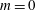$m=0$ and a blend of Orr and other mechanisms, such as lift-up, for other azimuthal wavenumbers. Further to this, velocity and pressure perturbations are shown to make up the optimal input and output showing that the thermoacoustic mechanism is crucial in large energy amplifications. For 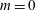$m=0$ these velocity perturbations are mainly longitudinal, but for higher wavenumbers azimuthal velocity fluctuations become prominent, especially in the non-swirling case. Sensitivity analyses are carried out with respect to the Mach number, Reynolds number and swirl number, and the accuracy of parametric gradients of the frequency response curve is assessed. The sensitivity analysis reveals that increases in Reynolds and Mach numbers yield higher gains, through a decrease in temperature diffusion. A rise in mean-flow swirl is shown to diminish the gain, with increased damping for higher azimuthal wavenumbers. This leads to a reordering of the most effectively amplified mode, with the axisymmetric (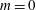$m=0$) mode becoming the dominant structure at moderate swirl numbers.

JFM classification

Mathematical Foundations: Computational methods Instability: Instability Reacting Flows: Reacting Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 859 , 25 January 2019 , pp. 516 - 542
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Åkervik, E., Brandt, L., Henningson, D. S., Hœpffner, J., Marxen, O. & Schlatter, P. 2006 Steady solutions of the Navier–Stokes equations by selective frequency damping. Phys. Fluids 18, 068102.Google Scholar
Berland, J., Bogey, C., Marsden, O. & Bailly, C. 2007 High-order, low dispersive and low dissipative explicit schemes for multiple-scale and boundary problems. J. Comput. Phys. 224 (2), 637–662.Google Scholar
Blanchard, M.2015 Linear and nonlinear dynamics of laminar premixed flames submitted to flow oscillations. PhD thesis, Ecole Polytechnique.Google Scholar
Blanchard, M., Schuller, T., Sipp, D. & Schmid, P. J. 2015 Response analysis of a laminar premixed M-flame to flow perturbations using a linearized compressible Navier–Stokes solver. Phys. Fluids 27 (4), 043602.Google Scholar
Candel, S., Durox, D., Schuller, T., Bourgouin, J.-F. & Moeck, J. P. 2014 Dynamics of swirling flames. Annu. Rev. Fluid Mech. 46 (1), 147–173.Google Scholar
Chu, B.-T. 1965 On the energy transfer to small disturbances in fluid flow (Part I). Acta Mech. 1 (3), 215–234.Google Scholar
Constantinescu, G. S. & Lele, S. K. 2002 A highly accurate technique for the treatment of flow equations at the polar axis in cylindrical coordinates using series expansions. J. Comput. Phys. 183 (1), 165–186.Google Scholar
Correa, S. M. 1998 Power generation and aeropropulsion gas turbines: from combustion science to combustion technology. In Symp. (International) on Combustion, vol. 27, pp. 1793–1807. Elsevier.Google Scholar
Crocco, L. 1951 Aspects of combustion stability in liquid propellant rocket motors, Part I: Fundamentals. Low frequency instability with monopropellants. J. Am. Rocket Soc. 21 (6), 163–178.Google Scholar
Culick, F. E. C. 1996 Combustion instabilities in propulsion systems. In Unsteady Combustion (ed. Culick, F., Heitor, M. V. & Whitelaw, J. H.). Springer.Google Scholar
Dowling, A. & Stow, S. 2003 Acoustic analysis of gas turbine combustors. J. Propul. Power 19, 751–764.Google Scholar
Fick, A. 1995 On liquid diffusion. J. Membr. Sci. 100 (1), 33–38.Google Scholar
Fosas de Pando, M. & Schmid, P. J. 2017 Optimal frequency-response sensitivity of compressible flow over roughness elements. J. Turbul. 18 (4), 338–351.Google Scholar
Fosas de Pando, M., Schmid, P. J. & Lele, S. K. 2014 Parametric sensitivity for large-scale aeroacoustic flows. Ctr. Turb. Res., Proc. of the Summer Program.Google Scholar
Fosas de Pando, M., Sipp, D. & Schmid, P. J. 2012 Efficient evaluation of the direct and adjoint linearized dynamics from compressible flow solvers. J. Comput. Phys. 231 (23), 7739–7755.Google Scholar
Garnaud, X.2012 Modes, transient dynamics and forced response of circular jets. PhD thesis, Ecole Polytechnique.Google Scholar
Garnaud, X., Lesshafft, L., Schmid, P. J. & Huerre, P. 2013 The preferred mode of incompressible jets: linear frequency response analysis. J. Fluid Mech. 716, 189–202.Google Scholar
Hernandez, V., Roman, J. E. & Vidal, V. 2005 SLEPc: a scalable and flexible toolkit for the solution of eigenvalue problems. ACM Trans. Math. Softw. 31 (3), 351–362.Google Scholar
Huang, Y. & Yang, V. 2005 Effect of swirl on combustion dynamics in a lean-premixed swirl-stabilized combustor. Proc. Combust. Inst. 30, 1775–1782.Google Scholar
Huang, Y. & Yang, V. 2009 Dynamics and stability of lean-premixed swirl-stabilized combustion. Prog. Energy Combust. Sci. 35 (4), 293–364.Google Scholar
Jeun, J., Nichols, J. W. & Jovanović, M. R. 2016 Input–output analysis of high-speed axisymmetric isothermal jet noise. Phys. Fluids 28 (4), 047101.Google Scholar
Juniper, M. P. 2011 Triggering in the horizontal Rijke tube: non-normality, transient growth and bypass transition. J. Fluid Mech. 667, 272–308.Google Scholar
Lieuwen, T. C. & Yang, V. 2005 Combustion Instabilities in Gas Turbine Engines: Operational Experience, Fundamental Mechanisms, and Modeling. Amer. Inst. Aeron. Astron.Google Scholar
Luchini, P. & Bottaro, A. 2014 Adjoint equations in stability analysis. Annu. Rev. Fluid Mech. 46, 493–517.Google Scholar
Mohseni, K. & Colonius, T. 2000 Numerical treatment of polar coordinate singularities. J. Comput. Phys. 157, 787–795.Google Scholar
Orr, W. M’F. 1907 The stability or instability of the steady motions of a perfect liquid and of a viscous liquid. Part I. A perfect liquid. Proc. R. Irish Acad. 27, 9–68.Google Scholar
Poinsot, T. J. & Lele, S. K. 1992 Boundary conditions for direct simulations of compressible viscous flows. J. Comput. Phys. 101 (1), 104–129.Google Scholar
Poinsot, T. J. & Veynante, D. 2012 Theoretical and Numerical Combustion, 3rd edn. R.T. Edwards.Google Scholar
Roy, A. & Govindarajan, R. 2010 An Introduction to Hydrodynamic Stability. Springer.Google Scholar
Sandberg, R. D.2007 Governing equations for a new compressible Navier–Stokes solver in general cylindrical coordinates. Project report, /eprints.soton.ac.uk/49523/. University of Southampton.Google Scholar
Schuller, T., Durox, D. & Candel, S. 2003 Self-induced combustion oscillations of laminar premixed flames stabilized on annular burners. Combust. Flame 135 (4), 525–537.Google Scholar
Skene, C. S. & Schmid, P. J. 2017 Parametric sensitivity analysis for premixed swirling M-flames. 24th Int. Congr. Sound and Vibr., ICSV 2017. Curran Assoc.Google Scholar
Sutherland, W. 1893 The viscosity of gases and molecular force. Lond. Edin. Dublin Philos. Mag. J. Sci. 36 (223), 507–531.Google Scholar
Trefethen, L. N., Trefethen, A. E., Reddy, S. C. & Driscoll, T. 1993 Hydrodynamic stability without eigenvalues. Science 261, 578–584.Google Scholar

Skene and Schmid supplementary movie 1

The optimal forcing for $\textit{St}=4.21$, $m=0$ ($u'$) shown for 15 time units.

Download Skene and Schmid supplementary movie 1(Video)
Video 3.1 MB

Skene and Schmid supplementary movie 2

The optimal output for $\textit{St}=4.21$, $m=0$ ($E'$) shown for 15 time units.

Download Skene and Schmid supplementary movie 2(Video)
Video 2.1 MB

Skene and Schmid supplementary movie 3

The optimal forcing for $\textit{St}=8.41$, $m=0$ ($u'$) shown for 15 time units.

Download Skene and Schmid supplementary movie 3(Video)
Video 3.2 MB

Skene and Schmid supplementary movie 4

The optimal output for $\textit{St}=8.41$, $m=0$ ($E'$) shown for 15 time units.

Download Skene and Schmid supplementary movie 4(Video)
Video 2.3 MB