Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-17T07:24:13.016Z Has data issue: false hasContentIssue false
  • English
  • Français

Adjoint sensitivity and optimal perturbations of the low-speed jet in cross-flow

Published online by Cambridge University Press:  22 August 2019

Marc A. Regan  and
Krishnan Mahesh Open the ORCID record for Krishnan Mahesh [Opens in a new window]
Marc A. Regan
Affiliation:
Department of Aerospace Engineering and Mechanics, University of Minnesota, Minneapolis, MN 55455, USA
Krishnan Mahesh
Affiliation:
Department of Aerospace Engineering and Mechanics, University of Minnesota, Minneapolis, MN 55455, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

The tri-global stability and sensitivity of the low-speed jet in cross-flow are studied using the adjoint equations and finite-time horizon optimal disturbance analysis at Reynolds number 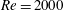$Re=2000$, based on the average velocity at the jet exit, the jet nozzle exit diameter and the kinematic viscosity of the jet, for two jet-to-cross-flow velocity ratios 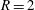$R=2$ and 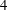$4$. A novel capability is developed on unstructured grids and parallel platforms for this purpose. Asymmetric modes are more important to the overall dynamics at 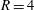$R=4$, suggesting increased sensitivity to experimental asymmetries at higher 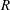$R$. Low-frequency modes show a connection to wake vortices. Adjoint modes show that the upstream shear layer is most sensitive to perturbations along the upstream side of the jet nozzle. Lower frequency downstream modes are sensitive in the cross-flow boundary layer. For 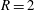$R=2$, optimal analysis reveals that for short time horizons, asymmetric perturbations dominate and grow along the counter-rotating vortex pair observed in the cross-section. However, as the time horizon increases, large transient growth is observed along the upstream shear layer. When 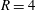$R=4$, the optimal perturbations for short time scales grow along the downstream shear layer. For long time horizons, they become hybrid modes that grow along both the upstream and downstream shear layers.

JFM classification

Instability: Absolute/convective instability Turbulent Flows: Turbulence simulation Wakes/Jets: Jets
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 877 , 25 October 2019 , pp. 330 - 372
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Present address: 110 Union Street SE, 107 Akerman Hall, Minneapolis, MN 55455, USA. Email address for correspondence: [email protected]

References

Åkervik, E., Brandt, L., Henningson, D. S., Hœpffner, J., Marxen, O. & Schlatter, P. 2006 Steady solutions of the Navier–Stokes equations by selective frequency damping. Phys. Fluids 18 (6), 068102.10.1063/1.2211705Google Scholar
Alves, L. S. D. B., Kelly, R. E. & Karagozian, A. R. 2008 Transverse-jet shear-layer instabilities. Part 2. Linear analysis for large jet-to-crossflow velocity ratio. J. Fluid Mech. 602, 383–401.10.1017/S002211200800102XGoogle Scholar
Arnoldi, W. E. 1951 The principle of minimized iteration in the solution of the matrix eigenproblem. Q. Appl. Maths 9, 17–29.10.1090/qam/42792Google Scholar
Babu, P. C. & Mahesh, K. 2004 Upstream entrainment in numerical simulations of spatially evolving round jets. Phys. Fluids 16 (10), 3699–3705.10.1063/1.1780548Google Scholar
Bagheri, S., Schlatter, P., Schmid, P. J. & Henningson, D. S. 2009 Global stability of a jet in crossflow. J. Fluid Mech. 624, 33–44.10.1017/S0022112009006053Google Scholar
Barkley, D. 2006 Linear analysis of the cylinder wake mean flow. Europhys. Lett. 75 (5), 750–756.10.1209/epl/i2006-10168-7Google Scholar
Barkley, D., Blackburn, H. M. & Sherwin, S. J. 2008 Direct optimal growth analysis for timesteppers. Intl J. Numer. Meth. Fluids 57, 1435–1458.10.1002/fld.1824Google Scholar
Cater, J. E. & Soria, J. 2002 The evolution of round zero-net-mass-flux jets. J. Fluid Mech. 472, 167–200.10.1017/S0022112002002264Google Scholar
Coelho, S. L. V. & Hunt, J. C. R. 1989 The dynamics of the near field of strong jets in crossflows. J. Fluid Mech. 200, 95–120.10.1017/S0022112089000583Google Scholar
Crighton, D. G. & Gaster, M. 1976 Stability of slowly diverging jet flow. J. Fluid Mech. 77, 397–413.10.1017/S0022112076002176Google Scholar
Davitian, J., Hendrickson, C., Getsinger, D., M’Closkey, R. T. & Karagozian, A. R. 2010 Strategic control of transverse jet shear layer instabilities. AIAA J. 48 (9), 2145–2156.10.2514/1.J050336Google Scholar
Eiff, O. S., Kawall, J. G. & Keffer, J. F. 1995 Lock-in of vortices in the wake of an elevated round turbulent jet in a crossflow. Exp. Fluids 19, 203–213.10.1007/BF00189709Google Scholar
Eroglu, A. & Breidenthal, R. E. 2001 Structure, penetration, and mixing of pulsed jets in crossflow. AIAA J. 39 (3), 417–423.10.2514/2.1351Google Scholar
Falgout, R. D. & Yang, U. M. 2002 HYPRE: a library of high performance preconditioners. In Computational Science ICCS 2002, pp. 632–641.10.1007/3-540-47789-6_66Google Scholar
Fric, T. F. & Roshko, A. 1994 Vortical structure in the wake of a transverse jet. J. Fluid Mech. 279, 1–47.10.1017/S0022112094003800Google Scholar
Getsinger, D. R., Gevorkyan, L., Smith, O. I. & Karagozian, A. R. 2014 Structural and stability characteristics of jets in crossflow. J. Fluid Mech. 760, 342–367.10.1017/jfm.2014.605Google Scholar
Giannetti, F. & Luchini, P. 2007 Structural sensitivity of the first instability of the cylinder wake. J. Fluid Mech. 581, 167–197.10.1017/S0022112007005654Google Scholar
Hill, D. C. 1995 Adjoint systems and their role in the receptivity problem for boundary layers. J. Fluid Mech. 292, 183–204.10.1017/S0022112095001480Google Scholar
Huerre, P. & Monkewitz, P. A. 1985 Absolute and convective instabilities in open shear layers. J. Fluid Mech. 159, 151–168.10.1017/S0022112085003147Google Scholar
Hunt, J. C. R., Wray, A. A. & Moin, P. 1988 Eddies, streams, and convergence zones in turbulent flows. In Center for Turbulence Res. Rep. CTR-S88, pp. 193–208.Google Scholar
Ilak, M., Schlatter, P., Bagheri, S. & Henningson, D. S. 2012 Bifurcation and stability analysis of a jet in cross-flow: onset of global instability at a low velocity ratio. J. Fluid Mech. 696, 94–121.10.1017/jfm.2012.10Google Scholar
Ince, E. L. 1926 Ordinary Differential Equations. Dover.Google Scholar
Iyer, P. S. & Mahesh, K. 2016 A numerical study of shear layer characteristics of low-speed transverse jets. J. Fluid Mech. 790, 275–307.10.1017/jfm.2016.7Google Scholar
Jordan, P. & Colonius, T. 2013 Wave packets and turbulent jet noise. Annu. Rev. Fluid Mech. 45, 173–195.10.1146/annurev-fluid-011212-140756Google Scholar
Juniper, M. P., Hanifi, A. & Theofilis, V. 2014 Modal stability theory lecture notes from the FLOW-NORDITA Summer School on advanced instability methods for complex flows, Stockholm, Sweden. Appl. Mech. Rev. 66 (2), 024804–024804–22.Google Scholar
Kamotani, Y. & Greber, I. 1972 Experiments on a turbulent jet in a cross flow. AIAA J. 10 (11), 1425–1429.10.2514/3.50386Google Scholar
Karagozian, A. R. 2010 Transverse jets and their control. Prog. Energy Combust. Sci. 36 (5), 531–553.10.1016/j.pecs.2010.01.001Google Scholar
Kelso, R. M., Lim, T. T. & Perry, A. E. 1996 An experimental study of round jets in cross-flow. J. Fluid Mech. 306, 111–144.10.1017/S0022112096001255Google Scholar
Kelso, R. M. & Smits, A. J. 1995 Horseshoe vortex systems resulting from the interaction between a laminar boundary layer and a transverse jet. Phys. Fluids 7, 153–158.10.1063/1.868736Google Scholar
Klotz, L., Gumowski, K. & Wesfreid, J. E. 2019 Experiments on a jet in a crossflow in the low-velocity-ratio regime. J. Fluid Mech. 863, 386–406.10.1017/jfm.2018.974Google Scholar
Krothapalli, A., Lourenco, L. & Buchlin, J. M. 1990 Separated flow upstream of a jet in a crossflow. AIAA J. 28 (3), 414–420.10.2514/3.10408Google Scholar
Lehoucq, R. B., Sorensen, D. C. & Yang, C. 1997 ARPACK Users’ Guide: Solution of Large Scale Eigenvalue Problems with Implicitly Restarted Arnoldi Methods.Google Scholar
Mahesh, K. 2013 The interaction of jets with crossflow. Annu. Rev. Fluid Mech. 45, 379–407.10.1146/annurev-fluid-120710-101115Google Scholar
Mahesh, K., Constantinescu, G. & Moin, P. 2004 A numerical method for large-eddy simulation in complex geometries. J. Comput. Phys. 197, 215–240.10.1016/j.jcp.2003.11.031Google Scholar
Mantič-Lugo, V., Arratia, C. & Gallaire, F. 2014 Self-consistent mean flow description of the nonlinear saturation of the vortex shedding in the cylinder wake. Phys. Rev. Lett. 113 (8), 084501.10.1103/PhysRevLett.113.084501Google Scholar
Margason, R. J. 1993 Fifty years of jet in cross flow research. In Aerospace Research & Development Conference 534, pp. 1–41.Google Scholar
M’Closkey, R. T., King, J. M., Cortelezzi, L. & Karagozian, A. R. 2002 The actively controlled jet in crossflow. J. Fluid Mech. 452, 325–335.10.1017/S0022112001006589Google Scholar
McMahon, H. M., Hester, D. D. & Palfery, J. G. 1971 Vortex shedding from a turbulent jet in a cross-wind. J. Fluid Mech. 48, 73–80.10.1017/S0022112071001472Google Scholar
Megerian, S., Davitian, J., Alves, L. S. d. B. & Karagozian, A. R. 2007 Transverse-jet shear-layer instabilities. Part 1. Experimental studies. J. Fluid Mech. 593, 93–129.10.1017/S0022112007008385Google Scholar
Morse, P. M. & Feshbach, H. 1953 Methods of Theoretical Physics. McGraw Hill.Google Scholar
Moussa, Z. M., Trischka, J. W. & Eskinazi, D. S. 1977 The near field in the mixing of a round jet with a cross-stream. J. Fluid Mech. 80, 49–80.10.1017/S0022112077001530Google Scholar
Muppidi, S. & Mahesh, K. 2005 Study of trajectories of jets in crossflow using direct numerical simulations. J. Fluid Mech. 530, 81–100.10.1017/S0022112005003514Google Scholar
Muppidi, S. & Mahesh, K. 2007 Direct numerical simulation of round turbulent jets in crossflow. J. Fluid Mech. 574, 59–84.10.1017/S0022112006004034Google Scholar
Muppidi, S. & Mahesh, K. 2008 Direct numerical simulation of passive scalar transport in transverse jets. J. Fluid Mech. 598, 335–360.10.1017/S0022112007000055Google Scholar
Narayanan, S., Barooah, P. & Cohen, J. M. 2003 Dynamics and control of an isolated jet in crossflow. AIAA J. 41 (12), 2316–2330.10.2514/2.6847Google Scholar
Peplinski, A., Schlatter, P. & Henningson, D. S. 2015 Global stability and optimal perturbation for a jet in cross-flow. Eur. J. Mech. (B/Fluids) 49, 438–447.10.1016/j.euromechflu.2014.06.001Google Scholar
Regan, M. A. & Mahesh, K. 2017 Global linear stability analysis of jets in cross-flow. J. Fluid Mech. 828, 812–836.10.1017/jfm.2017.489Google Scholar
Sau, R. & Mahesh, K. 2007 Passive scalar mixing in vortex rings. J. Fluid Mech. 582, 449–461.10.1017/S0022112007006349Google Scholar
Sau, R. & Mahesh, K. 2008 Dynamics and mixing of vortex rings in crossflow. J. Fluid Mech. 604, 389–409.10.1017/S0022112008001328Google Scholar
Sau, R. & Mahesh, K. 2010 Optimization of pulsed jets in crossflow. J. Fluid Mech. 653, 365–390.10.1017/S0022112010000388Google Scholar
Schmid, P. J. 2007 Nonmodal stability theory. Annu. Rev. Fluid Mech. 39, 129–162.10.1146/annurev.fluid.38.050304.092139Google Scholar
Shapiro, S. R., King, J., M’Closkey, R. T. & Karagozian, A. R. 2006 Optimization of controlled jets in crossflow. AIAA J. 44 (6), 1292–1298.10.2514/1.19457Google Scholar
Smith, S. H. & Mungal, M. G. 1998 Mixing, structure and scaling of the jet in crossflow. J. Fluid Mech. 357, 83–122.10.1017/S0022112097007891Google Scholar
Tammisola, O. & Juniper, M. P. 2016 Coherent structures in a swirl injector at Re = 4800 by nonlinear simulations and linear global modes. J. Fluid Mech. 792, 620–657.10.1017/jfm.2016.86Google Scholar
Theofilis, V. 2011 Global linear instability. Annu. Rev. Fluid Mech. 43, 319–352.10.1146/annurev-fluid-122109-160705Google Scholar
Turton, S. E., Tuckerman, L. S. & Barkley, D. 2015 Prediction of frequencies in thermosolutal convection from mean flows. Phys. Rev. E 91 (4), 1–10.Google Scholar
Vyazmina, E.2010 Bifurcations in a swirling flow. PhD thesis, École Polytechnique X.Google Scholar