1. Introduction
A body moving through a fluid experiences an additional inertia, or added mass, imparted to it by the flow that its motion generates within the fluid; see, among others, Kochin, Kibel’ & Roze (Reference Kochin, Kibel’ and Roze1964, § 7.7), Batchelor (Reference Batchelor1967, § 6.4), Lighthill (Reference Lighthill1986, § 8.3), Landau & Lifshitz (Reference Landau and Lifshitz1987, § 11), Saffman (Reference Saffman1992, § 5.1) and Newman (Reference Newman2017, §§ 4.12–4.14). The names ‘induced’ or ‘virtual’ mass are also used, though the latter is sometimes reserved for the sum of the actual and added masses (Milne-Thomson Reference Milne-Thomson1968, § 9.221; Newman Reference Newman2017, § 4.16).
Mathematically, added mass is linked to the irrotational dynamics of inviscid fluids. Consider a rigid body of surface ![]() $S$ and outward normal
$S$ and outward normal ![]() $\boldsymbol {n}$, represented in figure 1, translating at the velocity
$\boldsymbol {n}$, represented in figure 1, translating at the velocity ![]() $\boldsymbol {U}$ without rotation in a fluid of density
$\boldsymbol {U}$ without rotation in a fluid of density ![]() $\rho$. A flow of velocity potential
$\rho$. A flow of velocity potential ![]() $\phi$ is generated, satisfying the Laplace equation
$\phi$ is generated, satisfying the Laplace equation ![]() $\nabla ^2\phi = 0$ and the free-slip boundary condition
$\nabla ^2\phi = 0$ and the free-slip boundary condition ![]() $\partial \phi /\partial n = \boldsymbol {U}\boldsymbol {\cdot }\boldsymbol {n}$, with
$\partial \phi /\partial n = \boldsymbol {U}\boldsymbol {\cdot }\boldsymbol {n}$, with ![]() $\partial /\partial n = \boldsymbol {n}\boldsymbol {\cdot }\boldsymbol {\nabla }$ the normal derivative. The linearity of these equations implies a linear relation between
$\partial /\partial n = \boldsymbol {n}\boldsymbol {\cdot }\boldsymbol {\nabla }$ the normal derivative. The linearity of these equations implies a linear relation between ![]() $\boldsymbol {U}$ and
$\boldsymbol {U}$ and ![]() $\phi$. We write
$\phi$. We write ![]() $\phi = U_i\phi _i$, where the
$\phi = U_i\phi _i$, where the ![]() $\phi _i$, with
$\phi _i$, with ![]() $i = 1,2,3$, are functions of
$i = 1,2,3$, are functions of ![]() $\boldsymbol {x}$ dependent on
$\boldsymbol {x}$ dependent on ![]() $S$ and independent of
$S$ and independent of ![]() $\boldsymbol {U}$, satisfying the Laplace equation
$\boldsymbol {U}$, satisfying the Laplace equation ![]() $\nabla ^2\phi _i = 0$ and the boundary condition
$\nabla ^2\phi _i = 0$ and the boundary condition ![]() $\partial \phi _i/\partial n = n_i$; hereinafter the suffix notation is used, and summation over repeated suffixes is implied.
$\partial \phi _i/\partial n = n_i$; hereinafter the suffix notation is used, and summation over repeated suffixes is implied.

Figure 1. Dynamics of a rigid body in a homogeneous fluid.
Four quantities are of interest when describing the interaction between the fluid and the body: the impulse ![]() $\boldsymbol {I}$ and kinetic energy
$\boldsymbol {I}$ and kinetic energy ![]() $E$ of the fluid, given by
$E$ of the fluid, given by
and the hydrodynamic force ![]() $\boldsymbol {F}$ on the body and the dipole strength
$\boldsymbol {F}$ on the body and the dipole strength ![]() $\boldsymbol {\mathcal {D}}$ of this body, given by
$\boldsymbol {\mathcal {D}}$ of this body, given by
with ![]() $\boldsymbol {x}$ the position with respect to the body. Defining the symmetric and positive definite added mass tensor as
$\boldsymbol {x}$ the position with respect to the body. Defining the symmetric and positive definite added mass tensor as
we obtain
with ![]() $m_{f} = \rho \mathcal {V}$ the mass of the displaced fluid,
$m_{f} = \rho \mathcal {V}$ the mass of the displaced fluid, ![]() $\mathcal {V}$ the volume of the body and
$\mathcal {V}$ the volume of the body and ![]() $\delta _{ij}$ the Kronecker delta symbol. Accordingly, added mass characterizes the interaction between the body and the fluid fully.
$\delta _{ij}$ the Kronecker delta symbol. Accordingly, added mass characterizes the interaction between the body and the fluid fully.
When, in addition, the fluid supports the propagation of waves, such as acoustic waves (Lighthill Reference Lighthill1978, § 1.7) or surface gravity waves (Wehausen Reference Wehausen1971; Newman Reference Newman1978, Reference Newman2017, §§ 6.15–6.19), added mass becomes complex and varies with the frequency ![]() $\omega$. Its real part represents actual inertia and its imaginary part wave damping. Assuming temporal variations as
$\omega$. Its real part represents actual inertia and its imaginary part wave damping. Assuming temporal variations as ![]() $\exp (-\mathrm {i}\omega t)$ and introducing the inertial coefficients
$\exp (-\mathrm {i}\omega t)$ and introducing the inertial coefficients ![]() $\mu _{ij}(\omega ) = \mathrm {Re}\ m_{ij}(\omega )$ and the damping coefficients
$\mu _{ij}(\omega ) = \mathrm {Re}\ m_{ij}(\omega )$ and the damping coefficients ![]() $\lambda _{ij}(\omega ) = \omega\ \mathrm {Im}\ m_{ij}(\omega )$, the oscillations of a body of mass
$\lambda _{ij}(\omega ) = \omega\ \mathrm {Im}\ m_{ij}(\omega )$, the oscillations of a body of mass ![]() $m$ and position
$m$ and position ![]() $\boldsymbol {\xi }$ under the influence of an external force
$\boldsymbol {\xi }$ under the influence of an external force ![]() $\boldsymbol {F}^{e}$ satisfy the equation, in suffix notation,
$\boldsymbol {F}^{e}$ satisfy the equation, in suffix notation,
Because of causality, the two parts are Hilbert transforms of each other (Roddier Reference Roddier1971, § 13.1; Landau & Lifshitz Reference Landau and Lifshitz1980, § 123). Hence, they satisfy the relations introduced by Kramers and Kronig for the electric permittivity in 1926 and 1927 (Landau & Lifshitz Reference Landau and Lifshitz1984, §§ 77 and 82; Jackson Reference Jackson1999, § 7.10) and applied to added mass by Kotik & Mangulis (Reference Kotik and Mangulis1962).
When the body becomes small, viscosity comes into play. Its effect is governed, for a body of size ![]() $a$ oscillating in a fluid of kinematic viscosity
$a$ oscillating in a fluid of kinematic viscosity ![]() $\nu$, by the Stokes number
$\nu$, by the Stokes number ![]() $St = \omega a^2/\nu$ representing the ratio of the viscous time scale
$St = \omega a^2/\nu$ representing the ratio of the viscous time scale ![]() $a^2/\nu$ to the flow time scale
$a^2/\nu$ to the flow time scale ![]() $1/\omega$, or the squared ratio of the body size
$1/\omega$, or the squared ratio of the body size ![]() $a$ to the boundary-layer size
$a$ to the boundary-layer size ![]() $(\nu /\omega )^{1/2}$ (Batchelor Reference Batchelor1967, § 5.13; Landau & Lifshitz Reference Landau and Lifshitz1987, § 24). Added mass still exists but is accompanied by Stokes resistance and the Basset–Boussinesq force; see Landau & Lifshitz (Reference Landau and Lifshitz1987, § 24) for a sphere, and Lawrence & Weinbaum (Reference Lawrence and Weinbaum1986, Reference Lawrence and Weinbaum1988) and Zhang & Stone (Reference Zhang and Stone1998) for a spheroid.
$(\nu /\omega )^{1/2}$ (Batchelor Reference Batchelor1967, § 5.13; Landau & Lifshitz Reference Landau and Lifshitz1987, § 24). Added mass still exists but is accompanied by Stokes resistance and the Basset–Boussinesq force; see Landau & Lifshitz (Reference Landau and Lifshitz1987, § 24) for a sphere, and Lawrence & Weinbaum (Reference Lawrence and Weinbaum1986, Reference Lawrence and Weinbaum1988) and Zhang & Stone (Reference Zhang and Stone1998) for a spheroid.
Added mass plays an important role in practical applications, ranging from the small scales of particles and bubbles in dispersed two-phase flows (Magnaudet & Eames Reference Magnaudet and Eames2000) to the large scales of floats and ships in naval hydrodynamics (Wehausen Reference Wehausen1971; Newman Reference Newman1978, Reference Newman2017). Compendia of added masses for a variety of bodies have been given by Brennen (Reference Brennen1982), based in part on Kennard (Reference Kennard1967), and by Korotkin (Reference Korotkin2009).
The above is for homogeneous fluids. In the presence of density stratification, buoyancy gives rise to internal waves. Two stratifications have been considered in the literature. The first is uniform, a linear variation of density with depth. Added mass has been determined by Lai & Lee (Reference Lai and Lee1981) and Ermanyuk (Reference Ermanyuk2002) for a spheroid of vertical axis and Gorgui, Faltas & Ahmed (Reference Gorgui, Faltas and Ahmed1995) for a vertical plate, both oscillating. The force and moments on a horizontal elliptic cylinder have been calculated by Hurley (Reference Hurley1997) for translational oscillations and Hurley & Hood (Reference Hurley and Hood2001) for rotational oscillations. The force and moments on a horizontal disc have been calculated by Davis & Llewellyn Smith (Reference Davis and Llewellyn Smith2010) and Martin & Llewellyn Smith (Reference Martin and Llewellyn Smith2011) for a circular disc and Martin & Llewellyn Smith (Reference Martin and Llewellyn Smith2012) for an elliptic disc.
The second stratification is two layer, a homogeneous layer of light fluid atop another layer of heavier fluid. The layers may be semi-infinite, or have finite thicknesses with a rigid bottom and a rigid or free top surface. To determine added mass, multipole expansions have been applied to the oscillations of a horizontal circular cylinder located in either layer (Linton & McIver Reference Linton and McIver1995; Sturova Reference Sturova1999) or intersecting the interface between them (Motygin & Sturova Reference Motygin and Sturova2002), a sphere located in either layer (Cadby & Linton Reference Cadby and Linton2000) and a vertical circular cylinder spanning both layers (You, Shi & Miao Reference You, Shi and Miao2007). The hybrid element method, combining finite elements around the body and boundary elements away from it, has been applied to a horizontal elliptic cylinder located in the lower layer (Sturova Reference Sturova1994) or intersecting the interface (Sturova Reference Sturova2003; Sturova & Syui Reference Sturova and Syui2005). The boundary element method has been applied to a representation of a floating ship known as the Lewis form (Zilman, Kagan & Miloh Reference Zilman, Kagan and Miloh1996; Ten & Kashiwagi Reference Ten and Kashiwagi2004) and a rectangular box modelling a floating barge (Yeung & Nguyen Reference Yeung and Nguyen1999).
A uniformly stratified layer sandwiched between two homogeneous layers has been considered by Sturova (Reference Sturova1999, Reference Sturova2001, Reference Sturova2006) for a horizontal cylinder situated entirely in the bottom layer, entirely in the middle layer or spanning all three layers, respectively, and a uniformly stratified layer with a rigid bottom and an ice cover by Sturova (Reference Sturova2011).
All these studies are theoretical. Experimentally, building on the interpretation of added mass in the time domain as an impulse response function, introduced by Cummins (Reference Cummins1962) and Ogilvie (Reference Ogilvie1964) for surface gravity waves, Ermanyuk (Reference Ermanyuk2000) developed an original method for measuring added mass in the presence of internal waves, by applying an impulse to the body and deducing the frequency variations of its added mass from the Fourier analysis of the response. This method was applied by Ermanyuk (Reference Ermanyuk2000) and Ermanyuk & Gavrilov (Reference Ermanyuk and Gavrilov2002b) to cylinders of circular and diamond-shaped cross-sections, respectively, and Ermanyuk (Reference Ermanyuk2002) to oblate and prolate spheroids and a sphere; the oscillations were horizontal, the stratification uniform and the fluid effectively unbounded. The effect of finite depth was investigated by Ermanyuk & Gavrilov (Reference Ermanyuk and Gavrilov2002a) for a circular cylinder, Ermanyuk & Gavrilov (Reference Ermanyuk and Gavrilov2003) for a sphere and Brouzet et al. (Reference Brouzet, Ermanyuk, Moulin, Pillet and Dauxois2017) for a circular cylinder, a vertical plate and a flat-top hill. A Lewis form in a two-layer fluid was considered by Ten & Kashiwagi (Reference Ten and Kashiwagi2004).
The present study proposes a general approach of added mass for internal waves in uniform stratification. All the work cited above calculated added mass for specific bodies oscillating in specific directions, except for Ermanyuk (Reference Ermanyuk2002) and Ermanyuk & Gavrilov (Reference Ermanyuk and Gavrilov2002b), who presented a general analysis of added mass in the frequency domain, introducing anisotropic coordinate stretching and analytic continuation in frequency so as to relate the added mass of the original body in a stratified fluid to the added mass of the stretched version of the same body in a homogenous fluid. Here, added mass is considered for arbitrary motion of an arbitrary body, both in the time domain and in the frequency domain, and its relation to the various quantities of interest for the dynamics of the body is investigated. Added mass is also related to the boundary integral representation of the body, considered in Voisin (Reference Voisin2021). Early versions of smaller scope were presented in summary form by Voisin (Reference Voisin2007, Reference Voisin2009). In order to keep the analysis tractable, a number of approximations are made: the fluid is unbounded, uniformly stratified, inviscid, non-diffusive and non-rotating, the Boussinesq approximation is valid, the waves are linear and the body performs translational motion without rotation. The present paper, hereafter referred to as Part 1, investigates the general properties of added mass and discusses two particular cases: the elliptic cylinder of horizontal axis as a typical two-dimensional body, and the spheroid of vertical axis as a typical three-dimensional body. A companion paper (Voisin Reference Voisin2024), the associated Part 2, discusses how past experiments from the literature, involving the oscillation of buoyant bodies about their equilibrium position, may be explained in terms of added mass.
The equations of motion are set in § 2. The hydrostatic response of the fluid is analysed in § 3. For its hydrodynamic response, the modifications to the quantities (1.1)–(1.2) because of the stratification are analysed in § 4, giving two possible definitions of added mass. Consideration of the properties of each leads to the choice of one. The frequency variations of added mass are presented in § 5 for the cylinder and the spheroid, and applied to the wave power, known as a ‘conversion rate’ within the context of the oceanic internal tide. The temporal aspects of added mass, including the Kramers–Kronig relations, are analysed in § 6. The changes to added mass because of the stratification are interpreted as the addition of a new memory force on the moving body. The main conclusions are summarized in § 7 where their relation to the literature is also discussed.
2. Equations of motion
We are concerned with small disturbances to the state of rest of a stratified fluid where the density distribution ![]() $\rho _0(z)$ and the pressure distribution
$\rho _0(z)$ and the pressure distribution ![]() $p_0(z)$ satisfy
$p_0(z)$ satisfy
respectively the hydrostatic law and the definition of the buoyancy frequency ![]() $N$, with
$N$, with ![]() $z$ the upward vertical coordinate,
$z$ the upward vertical coordinate, ![]() $g$ the acceleration due to gravity and
$g$ the acceleration due to gravity and ![]() $\rho _{00}$ a reference density. The stratification is assumed uniform, such that
$\rho _{00}$ a reference density. The stratification is assumed uniform, such that ![]() $N$ is a constant, and the Boussinesq approximation is made, according to which the density variations are small and generate buoyancy forces but no inertial forces. The disturbances
$N$ is a constant, and the Boussinesq approximation is made, according to which the density variations are small and generate buoyancy forces but no inertial forces. The disturbances ![]() $\boldsymbol {u} = (u,v,w)$ in velocity,
$\boldsymbol {u} = (u,v,w)$ in velocity, ![]() $p$ in pressure and
$p$ in pressure and ![]() $\rho$ in density satisfy the linearized equations of motion, namely the Euler equation
$\rho$ in density satisfy the linearized equations of motion, namely the Euler equation
the equation of continuity
and the equation of state
expressing the incompressibility condition ![]() $\mathrm {d}(\rho _0+\rho )/\mathrm {d}t = 0$. Cartesian coordinates
$\mathrm {d}(\rho _0+\rho )/\mathrm {d}t = 0$. Cartesian coordinates ![]() $(x,y,z)$ are used, with unit vectors
$(x,y,z)$ are used, with unit vectors ![]() $(\boldsymbol {e}_x,\boldsymbol {e}_y,\boldsymbol {e}_z)$. Time is denoted by
$(\boldsymbol {e}_x,\boldsymbol {e}_y,\boldsymbol {e}_z)$. Time is denoted by ![]() $t$, position by
$t$, position by ![]() $\boldsymbol {x} = (x,y,z)$ and the del operator by
$\boldsymbol {x} = (x,y,z)$ and the del operator by ![]() $\boldsymbol {\nabla } = (\partial /\partial x,\partial /\partial y,\partial /\partial z)$.
$\boldsymbol {\nabla } = (\partial /\partial x,\partial /\partial y,\partial /\partial z)$.
The equations are solved by introducing the pseudopotential ![]() $\psi$, sometimes called an ‘internal potential’, in terms of which the fluid dynamical quantities are expressed as
$\psi$, sometimes called an ‘internal potential’, in terms of which the fluid dynamical quantities are expressed as
The potential satisfies the wave equation
where ![]() $\boldsymbol {\nabla }_{h} = (\partial /\partial x,\partial /\partial y,0)$. It was introduced by Sobolev (Reference Sobolev1954) for inertial waves and Gorodtsov & Teodorovich (Reference Gorodtsov and Teodorovich1980) for internal waves; see Voisin (Reference Voisin1991) for a brief derivation and Voisin (Reference Voisin2021) for an updated bibliography.
$\boldsymbol {\nabla }_{h} = (\partial /\partial x,\partial /\partial y,0)$. It was introduced by Sobolev (Reference Sobolev1954) for inertial waves and Gorodtsov & Teodorovich (Reference Gorodtsov and Teodorovich1980) for internal waves; see Voisin (Reference Voisin1991) for a brief derivation and Voisin (Reference Voisin2021) for an updated bibliography.
3. Hydrostatic response
We consider the translation of a rigid body of volume ![]() $\mathcal {V}$ and mass
$\mathcal {V}$ and mass ![]() $m$, represented in figure 2, at the velocity
$m$, represented in figure 2, at the velocity ![]() $\boldsymbol {U}$. The response of the fluid comprises two parts, one hydrostatic and the other hydrodynamic. We look briefly at the hydrostatic response in this section.
$\boldsymbol {U}$. The response of the fluid comprises two parts, one hydrostatic and the other hydrodynamic. We look briefly at the hydrostatic response in this section.

Figure 2. Dynamics of a rigid body in a stratified fluid.
The quantity of interest is the pressure force exerted on the body,
with ![]() $S$ the surface of the body and
$S$ the surface of the body and ![]() $\boldsymbol {n}$ its outward normal. Application of Gauss’ theorem and use of (2.1a) give
$\boldsymbol {n}$ its outward normal. Application of Gauss’ theorem and use of (2.1a) give
namely Archimedes’ force, where ![]() $V$ is the region of fluid occupied by the body and
$V$ is the region of fluid occupied by the body and ![]() $m_{f} = \int _V\rho _0(z)\,\mathrm {d}^3x$ is the mass of the displaced fluid.
$m_{f} = \int _V\rho _0(z)\,\mathrm {d}^3x$ is the mass of the displaced fluid.
We set ![]() $z = 0$ at the level where the body is neutrally buoyant, namely where its weight balances Archimedes’ force, and we introduce the position
$z = 0$ at the level where the body is neutrally buoyant, namely where its weight balances Archimedes’ force, and we introduce the position ![]() $\zeta$ of its centroid with respect to this level, such that
$\zeta$ of its centroid with respect to this level, such that ![]() $\mathcal {V}\zeta = \int _V z\,\mathrm {d}^3x$. Writing, by (2.1b),
$\mathcal {V}\zeta = \int _V z\,\mathrm {d}^3x$. Writing, by (2.1b),
we obtain ![]() $m = \rho _0(0)\mathcal {V}$ and
$m = \rho _0(0)\mathcal {V}$ and
Similar derivations may be found in Larsen (Reference Larsen1969) and Lai & Lee (Reference Lai and Lee1981).
4. Hydrodynamic response
The hydrodynamic response is due to the free-slip forcing at ![]() $S$, namely, using (2.5a),
$S$, namely, using (2.5a),
where ![]() $\partial /\partial n = \boldsymbol {n}\boldsymbol {\cdot }\boldsymbol {\nabla }$ and
$\partial /\partial n = \boldsymbol {n}\boldsymbol {\cdot }\boldsymbol {\nabla }$ and ![]() $\partial /\partial n_{h} = \boldsymbol {n}\boldsymbol {\cdot }\boldsymbol {\nabla }_{h}$. With
$\partial /\partial n_{h} = \boldsymbol {n}\boldsymbol {\cdot }\boldsymbol {\nabla }_{h}$. With ![]() $S$ a moving surface, this forcing is not linear. For it to become so, an assumption of a small displacement of the body compared with its size must be introduced, allowing
$S$ a moving surface, this forcing is not linear. For it to become so, an assumption of a small displacement of the body compared with its size must be introduced, allowing ![]() $S$ to be considered fixed.
$S$ to be considered fixed.
Stokes (Reference Stokes1851, § 41), however, pointed out that this assumption may be relaxed. For the flow of a homogeneous viscous fluid, at small velocities ![]() $\boldsymbol {U}$ of the body and
$\boldsymbol {U}$ of the body and ![]() $\boldsymbol {u}$ of the fluid, he noted that the switch to a system of coordinates moving with the body leaves the linear equations of motion unchanged – since the convective terms associated with the switch are of second order in the small velocities – and makes
$\boldsymbol {u}$ of the fluid, he noted that the switch to a system of coordinates moving with the body leaves the linear equations of motion unchanged – since the convective terms associated with the switch are of second order in the small velocities – and makes ![]() $S$ fixed. Gatignol (Reference Gatignol1983) and Maxey & Riley (Reference Maxey and Riley1983) implemented the switch analytically. The boundary condition becomes linear, without requiring small displacements. The results may thus be applied to a body moving along an arbitrary path.
$S$ fixed. Gatignol (Reference Gatignol1983) and Maxey & Riley (Reference Maxey and Riley1983) implemented the switch analytically. The boundary condition becomes linear, without requiring small displacements. The results may thus be applied to a body moving along an arbitrary path.
The same is true here: with ![]() $\boldsymbol {\xi }(t)$ the position of the body and
$\boldsymbol {\xi }(t)$ the position of the body and ![]() $\boldsymbol {U}(t) = \mathrm {d}\boldsymbol {\xi }/\mathrm {d}t$ its velocity, assumed small, a switch to the coordinates
$\boldsymbol {U}(t) = \mathrm {d}\boldsymbol {\xi }/\mathrm {d}t$ its velocity, assumed small, a switch to the coordinates ![]() $\boldsymbol {x'} = \boldsymbol {x}-\boldsymbol {\xi }(t)$ and
$\boldsymbol {x'} = \boldsymbol {x}-\boldsymbol {\xi }(t)$ and ![]() $t' = t$ gives
$t' = t$ gives
yielding additional terms ![]() $\rho _{00}\boldsymbol {U}\boldsymbol {\cdot }\boldsymbol {\nabla }'\boldsymbol {u}$ in (2.2) and
$\rho _{00}\boldsymbol {U}\boldsymbol {\cdot }\boldsymbol {\nabla }'\boldsymbol {u}$ in (2.2) and ![]() $\boldsymbol {U}\boldsymbol {\cdot }\boldsymbol {\nabla }'\!\rho$ in (2.4), both negligible. In the following we omit the primes and take (2.2)–(2.4) as our equations of motion and (4.1) as our boundary condition, on the understanding that
$\boldsymbol {U}\boldsymbol {\cdot }\boldsymbol {\nabla }'\!\rho$ in (2.4), both negligible. In the following we omit the primes and take (2.2)–(2.4) as our equations of motion and (4.1) as our boundary condition, on the understanding that ![]() $S$ is fixed. This will allow the application of the results to a body moving along an arbitrary path in § 6.2.
$S$ is fixed. This will allow the application of the results to a body moving along an arbitrary path in § 6.2.
Now, the linearity of (2.6) and (4.1) implies a linear relation between the forcing ![]() $\boldsymbol {U}(t)$ and its effect
$\boldsymbol {U}(t)$ and its effect ![]() $\psi (\boldsymbol {x},t)$. The most general such relation is a temporal convolution (Landau & Lifshitz Reference Landau and Lifshitz1980, § 123, Reference Landau and Lifshitz1984, § 77; Jackson Reference Jackson1999, § 7.10) of the form
$\psi (\boldsymbol {x},t)$. The most general such relation is a temporal convolution (Landau & Lifshitz Reference Landau and Lifshitz1980, § 123, Reference Landau and Lifshitz1984, § 77; Jackson Reference Jackson1999, § 7.10) of the form
with ![]() $\ast$ the convolution operator. Hereinafter the suffix notation is used, with
$\ast$ the convolution operator. Hereinafter the suffix notation is used, with ![]() $i$ ranging over
$i$ ranging over ![]() $1$,
$1$, ![]() $2$ and the vertical direction
$2$ and the vertical direction ![]() $3$, and summation over repeated suffixes is implied. The
$3$, and summation over repeated suffixes is implied. The ![]() $\psi _i$ are functions of
$\psi _i$ are functions of ![]() $\boldsymbol {x}$ and
$\boldsymbol {x}$ and ![]() $t$ dependent on
$t$ dependent on ![]() $S$ and independent of
$S$ and independent of ![]() $\boldsymbol {U}$. They satisfy the wave equation
$\boldsymbol {U}$. They satisfy the wave equation
and the boundary condition
with ![]() $\delta (t)$ the Dirac delta function. They represent the internal potential due to a unit velocity impulse
$\delta (t)$ the Dirac delta function. They represent the internal potential due to a unit velocity impulse ![]() $U_i(t) = \delta (t)$ along the
$U_i(t) = \delta (t)$ along the ![]() $x_i$ direction, or a unit step displacement
$x_i$ direction, or a unit step displacement ![]() $\xi _i(t) = H(t)$ with
$\xi _i(t) = H(t)$ with ![]() $H(t)$ the Heaviside step function.
$H(t)$ the Heaviside step function.
We investigate now the four quantities involved in the definition of added mass, discussed in § 1, for convenience in a different order.
4.1. Hydrodynamic force
The hydrodynamic force on the body is
namely, by (2.5),
Use of (4.3) yields
where
or equivalently
constitutes a first possible definition of added mass, introduced by Ermanyuk (Reference Ermanyuk2002) and Ermanyuk & Gavrilov (Reference Ermanyuk and Gavrilov2002b) in monochromatic form.
4.2. Wave energy
The scalar product of ![]() $\boldsymbol {u}$ with (2.2), combined with (2.3) and (2.4), provides the energy conservation equation
$\boldsymbol {u}$ with (2.2), combined with (2.3) and (2.4), provides the energy conservation equation
Accordingly, ![]() $\rho _{00}\boldsymbol {u}^2/2+g^2\rho ^2/2\rho _{00}N^2$ is the wave energy density, combining kinetic and potential energy, and
$\rho _{00}\boldsymbol {u}^2/2+g^2\rho ^2/2\rho _{00}N^2$ is the wave energy density, combining kinetic and potential energy, and ![]() $p\boldsymbol {u}$ the wave energy flux, namely a vector whose scalar product with
$p\boldsymbol {u}$ the wave energy flux, namely a vector whose scalar product with ![]() $\boldsymbol {n}$ represents the rate at which energy is transported across a unit surface element of normal
$\boldsymbol {n}$ represents the rate at which energy is transported across a unit surface element of normal ![]() $\boldsymbol {n}$.
$\boldsymbol {n}$.
The total power output of the body follows from integrating this flux over ![]() $S$, to give
$S$, to give
that is,
The same added mass tensor is involved as for the hydrodynamic force, consistent with the fact that the energy of the fluid varies in response to the work of the hydrodynamic force ![]() $-\boldsymbol {F}$ exerted by the body on the fluid.
$-\boldsymbol {F}$ exerted by the body on the fluid.
4.3. Wave momentum
Momentum conservation is written in flux form, by (2.2) and (2.5), as
where
with ![]() $\delta _{ij}$ the Kronecker delta symbol, is the wave momentum flux, namely a tensor whose contraction with
$\delta _{ij}$ the Kronecker delta symbol, is the wave momentum flux, namely a tensor whose contraction with ![]() $\boldsymbol {n}$ represents the rate at which momentum is transported across a unit surface element of normal
$\boldsymbol {n}$ represents the rate at which momentum is transported across a unit surface element of normal ![]() $\boldsymbol {n}$.
$\boldsymbol {n}$.
The total momentum output of the body follows as
with ![]() $\boldsymbol {n}_{h}$ the horizontal projection of
$\boldsymbol {n}_{h}$ the horizontal projection of ![]() $\boldsymbol {n}$, namely
$\boldsymbol {n}$, namely
where
or equivalently
constitutes a second possible definition of added mass. Consistent with (4.15), the difference between the two definitions follows from the fact that not only pressure but also buoyancy contribute to changing the momentum of the fluid.
4.4. Dipole strength
The dipole strength of the body may be derived from a Kirchhoff–Helmholtz integral, by expanding this integral at large distances from the body; see Batchelor (Reference Batchelor1967, §§ 2.9 and 6.4) and Lighthill (Reference Lighthill1986, §§ 8.1–8.3) for fluid flow, and Pierce (Reference Pierce2019, § 4.6) for acoustic waves. The integral and its expansion are obtained for internal waves in Appendix B, using the Green's function introduced in Appendix A. Arbitrary forcing within a surface ![]() $S$ of outward normal
$S$ of outward normal ![]() $\boldsymbol {n}$, generating the internal potential
$\boldsymbol {n}$, generating the internal potential ![]() $\psi$ and the normal velocity
$\psi$ and the normal velocity ![]() $u_n = \boldsymbol {n}\boldsymbol {\cdot }\boldsymbol {u}$ at the surface, has the monopole strength
$u_n = \boldsymbol {n}\boldsymbol {\cdot }\boldsymbol {u}$ at the surface, has the monopole strength
and the dipole strength
For a rigid body, we have ![]() $\int _S n_i\,\mathrm {d}^2S = 0$ and
$\int _S n_i\,\mathrm {d}^2S = 0$ and ![]() $\int _S x_in_j\,\mathrm {d}^2S = \mathcal {V}\delta _{ij}$. Accordingly,
$\int _S x_in_j\,\mathrm {d}^2S = \mathcal {V}\delta _{ij}$. Accordingly,
with ![]() $m_{f} = \rho _{00}\mathcal {V}$ the mass of the displaced fluid, so that
$m_{f} = \rho _{00}\mathcal {V}$ the mass of the displaced fluid, so that
an expression of the dipole strength involving the same added mass tensor as for the wave momentum.
4.5. Symmetry
In order to decide which definition of added mass is the most relevant – ![]() $m_{ij}$ given by (4.9)–(4.10) or
$m_{ij}$ given by (4.9)–(4.10) or ![]() $m'_{ij}$ given by (4.18)–(4.19) – we start by looking at their symmetry. The Green's theorem (B2) is applied to the volume delimited by the surface
$m'_{ij}$ given by (4.18)–(4.19) – we start by looking at their symmetry. The Green's theorem (B2) is applied to the volume delimited by the surface ![]() $S$ of the body and a sphere
$S$ of the body and a sphere ![]() $S_R$ of large radius
$S_R$ of large radius ![]() $R$, and to the time range
$R$, and to the time range ![]() $\mathopen{]}-\infty,+\infty\mathclose{[}$. The functions are chosen as
$\mathopen{]}-\infty,+\infty\mathclose{[}$. The functions are chosen as ![]() $\psi _i$ and
$\psi _i$ and ![]() $\psi _j$. These are zero at
$\psi _j$. These are zero at ![]() $t = -\infty$, and their temporal derivatives vanish as
$t = -\infty$, and their temporal derivatives vanish as ![]() $t \to +\infty$, consistent with the behaviours exhibited later in § 6.2 for the impulse response functions. Accordingly, the initial and final contributions vanish. The body, being rigid, acts as a dipole, so that
$t \to +\infty$, consistent with the behaviours exhibited later in § 6.2 for the impulse response functions. Accordingly, the initial and final contributions vanish. The body, being rigid, acts as a dipole, so that ![]() $\psi _i$ and
$\psi _i$ and ![]() $\psi _j$ decrease as
$\psi _j$ decrease as ![]() $1/R^2$ and their gradients as
$1/R^2$ and their gradients as ![]() $1/R^3$. The contribution of
$1/R^3$. The contribution of ![]() $S_R$ vanishes, and we obtain
$S_R$ vanishes, and we obtain
 \begin{align} &\int\,\mathrm{d}t\int_V\,\mathrm{d}^3x \left[ \psi_i\left(\frac{\partial^2}{\partial t^2}\nabla^2+N^2\nabla_{h}^2\right)\psi_j- \psi_j\left(\frac{\partial^2}{\partial t^2}\nabla^2+N^2\nabla_{h}^2\right)\psi_i \right] \nonumber\\ &\quad ={-}\int\,\mathrm{d}t\int_S\,\mathrm{d}^2S\, \left[ \psi_i \left( \frac{\partial^2}{\partial t^2}\frac{\partial}{\partial n}+N^2\frac{\partial}{\partial n_{h}} \right) \psi_j - \psi_j \left( \frac{\partial^2}{\partial t^2}\frac{\partial}{\partial n}+N^2\frac{\partial}{\partial n_{h}} \right) \psi_i \right], \end{align}
\begin{align} &\int\,\mathrm{d}t\int_V\,\mathrm{d}^3x \left[ \psi_i\left(\frac{\partial^2}{\partial t^2}\nabla^2+N^2\nabla_{h}^2\right)\psi_j- \psi_j\left(\frac{\partial^2}{\partial t^2}\nabla^2+N^2\nabla_{h}^2\right)\psi_i \right] \nonumber\\ &\quad ={-}\int\,\mathrm{d}t\int_S\,\mathrm{d}^2S\, \left[ \psi_i \left( \frac{\partial^2}{\partial t^2}\frac{\partial}{\partial n}+N^2\frac{\partial}{\partial n_{h}} \right) \psi_j - \psi_j \left( \frac{\partial^2}{\partial t^2}\frac{\partial}{\partial n}+N^2\frac{\partial}{\partial n_{h}} \right) \psi_i \right], \end{align}We thus have
implying that the first definition of added mass is symmetric while the second is not. This provides a first hint that ![]() $m_{ij}$ may be the best choice.
$m_{ij}$ may be the best choice.
4.6. Monochromatic case
Now, the situations investigated in practice are often monochromatic, either because the forcing is of this type, or because temporal Fourier transforms are used. We define direct and inverse transforms according to
The added masses (4.9) and (4.18) have the transforms
respectively, and are related to each other by
We consider waves of frequency ![]() $\omega$, varying with time through the factor
$\omega$, varying with time through the factor ![]() $\exp (-\mathrm {i}\omega t)$ that is suppressed in the following. For this, the body is assumed to oscillate at the velocity
$\exp (-\mathrm {i}\omega t)$ that is suppressed in the following. For this, the body is assumed to oscillate at the velocity ![]() $\boldsymbol{U}\exp(-\mathrm{i}\omega t)$, where the instant
$\boldsymbol{U}\exp(-\mathrm{i}\omega t)$, where the instant ![]() $t= 0$ is chosen such that the components
$t= 0$ is chosen such that the components ![]() $U_i$ of
$U_i$ of ![]() $\boldsymbol{U}$ are real and positive. The linear fluid dynamical quantities become
$\boldsymbol{U}$ are real and positive. The linear fluid dynamical quantities become
and have zero phase average. Wave power is a quadratic quantity. Decomposing the tensor ![]() $m_{ij}(\omega )$ into an inertial part
$m_{ij}(\omega )$ into an inertial part ![]() $\mu _{ij}(\omega )$ and a wave damping part
$\mu _{ij}(\omega )$ and a wave damping part ![]() $\lambda _{ij}(\omega )$, such that
$\lambda _{ij}(\omega )$, such that
and using the result that the product of two quantities of complex amplitudes ![]() $A$ and
$A$ and ![]() $B$ has the phase average
$B$ has the phase average ![]() $\mathrm {Re}[A\bar {B}]/2$, where the overbar denotes a complex conjugate, the average wave power follows as
$\mathrm {Re}[A\bar {B}]/2$, where the overbar denotes a complex conjugate, the average wave power follows as
This quadratic form, representing energy dissipation, is necessarily positive definite, implying that the tensor ![]() $\lambda _{ij}(\omega )$ is also positive definite.
$\lambda _{ij}(\omega )$ is also positive definite.
4.7. Which added mass?
The first definition of added mass, ![]() $m_{ij}$, thus appears as the most relevant. It is symmetric while the second definition,
$m_{ij}$, thus appears as the most relevant. It is symmetric while the second definition, ![]() $m'_{ij}$, is not. The two quantities expressed in terms of it – the hydrodynamic force and the wave energy – are the most interesting in practice. By contrast, the two quantities expressed in terms of
$m'_{ij}$, is not. The two quantities expressed in terms of it – the hydrodynamic force and the wave energy – are the most interesting in practice. By contrast, the two quantities expressed in terms of ![]() $m'_{ij}$ are of meagre interest: the wave momentum has zero phase average, and one must switch to the pseudomomentum to get actual momentum transport (Bühler Reference Bühler2014); monochromatic waves propagate in beams along which, whatever the distance, the wave profile still depends on the details of the forcing, not on its dipole strength alone (Lighthill Reference Lighthill1978, § 4.10; Voisin Reference Voisin2003).
$m'_{ij}$ are of meagre interest: the wave momentum has zero phase average, and one must switch to the pseudomomentum to get actual momentum transport (Bühler Reference Bühler2014); monochromatic waves propagate in beams along which, whatever the distance, the wave profile still depends on the details of the forcing, not on its dipole strength alone (Lighthill Reference Lighthill1978, § 4.10; Voisin Reference Voisin2003).
In the following we define added mass as ![]() $m_{ij}$, but still use
$m_{ij}$, but still use ![]() $m'_{ij}$ to determine it. Specifically, the boundary integral method (Voisin Reference Voisin2021) provides a representation of an oscillating body as a source term
$m'_{ij}$ to determine it. Specifically, the boundary integral method (Voisin Reference Voisin2021) provides a representation of an oscillating body as a source term ![]() $q(\boldsymbol {x})$ in the wave equation (2.6), and from it the dipole strength
$q(\boldsymbol {x})$ in the wave equation (2.6), and from it the dipole strength
Once this strength is known, so is ![]() $m'_{ij}(\omega )$ by (4.31c), then
$m'_{ij}(\omega )$ by (4.31c), then ![]() $m_{ij}(\omega )$ by (4.30).
$m_{ij}(\omega )$ by (4.30).
5. Frequency-dependent aspects
5.1. Added mass
We consider now the added mass coefficients
of typical oscillating bodies: an elliptic cylinder of horizontal axis in two dimensions, and a spheroid of vertical axis in three dimensions. Single-layer representations ![]() $q(\boldsymbol {x})$ of these bodies were given in table 5 of Voisin (Reference Voisin2021), along with their spectra
$q(\boldsymbol {x})$ of these bodies were given in table 5 of Voisin (Reference Voisin2021), along with their spectra ![]() $q(\boldsymbol {k})$. Expanding these at small wavenumber, as
$q(\boldsymbol {k})$. Expanding these at small wavenumber, as
provides immediately the dipole strengths ![]() $\boldsymbol {\mathcal {D}}$ and from them the added masses.
$\boldsymbol {\mathcal {D}}$ and from them the added masses.
The cylinder is assumed to have horizontal ![]() $y$ axis and semi-axes
$y$ axis and semi-axes ![]() $a$ and
$a$ and ![]() $b$ in the vertical
$b$ in the vertical ![]() $(x,z)$ plane, respectively, and to oscillate at the velocity
$(x,z)$ plane, respectively, and to oscillate at the velocity ![]() $(U,0,W)\exp (-\mathrm {i}\omega t)$. We obtain, per unit length along the
$(U,0,W)\exp (-\mathrm {i}\omega t)$. We obtain, per unit length along the ![]() $y$ direction,
$y$ direction,
where
 \begin{equation} \varUpsilon = \epsilon \left(1-\frac{1}{\varOmega^2}\right)^{1/2}, \end{equation}
\begin{equation} \varUpsilon = \epsilon \left(1-\frac{1}{\varOmega^2}\right)^{1/2}, \end{equation}
with ![]() $\epsilon = b/a$ the aspect ratio and
$\epsilon = b/a$ the aspect ratio and ![]() $\varOmega = \omega /N$ the frequency ratio. The added mass coefficients are given in table 1 for the elliptic cylinder and its particular cases: the circular cylinder (
$\varOmega = \omega /N$ the frequency ratio. The added mass coefficients are given in table 1 for the elliptic cylinder and its particular cases: the circular cylinder (![]() $\epsilon = 1$), the horizontal plate (
$\epsilon = 1$), the horizontal plate (![]() $\epsilon = 0$) and the vertical plate (
$\epsilon = 0$) and the vertical plate (![]() $\epsilon = \infty$). The coordinates axes are principal axes and the added mass tensor is diagonal, leading to the simplified notations
$\epsilon = \infty$). The coordinates axes are principal axes and the added mass tensor is diagonal, leading to the simplified notations ![]() $C_x = C_{11}$ and
$C_x = C_{11}$ and ![]() $C_z = C_{33}$.
$C_z = C_{33}$.
Table 1. Added mass coefficients for the elliptic cylinder and the spheroid, together with their values for aspects ratios ![]() $\epsilon = 0$,
$\epsilon = 0$, ![]() $1$ and
$1$ and ![]() $\infty$ and their limit for frequency ratio
$\infty$ and their limit for frequency ratio ![]() $\varOmega \to \infty$. The quantities
$\varOmega \to \infty$. The quantities ![]() $\varUpsilon$ and
$\varUpsilon$ and ![]() $D(\varUpsilon )$ are defined in (5.4) and (5.7), respectively.
$D(\varUpsilon )$ are defined in (5.4) and (5.7), respectively.

Consistent with causality, the coefficients are analytic functions in the upper half of the complex ![]() $\varOmega$ plane. The branch cuts emanating from the branch points
$\varOmega$ plane. The branch cuts emanating from the branch points ![]() $\varOmega = \pm 1$ are taken vertically downwards, yielding
$\varOmega = \pm 1$ are taken vertically downwards, yielding
along the real ![]() $\varOmega$ axis.
$\varOmega$ axis.
For the spheroid, of vertical ![]() $z$ axis and semi-axes
$z$ axis and semi-axes ![]() $a$ and
$a$ and ![]() $b$ along the horizontal and the vertical, respectively, oscillating at the same velocity, the dipole strength is
$b$ along the horizontal and the vertical, respectively, oscillating at the same velocity, the dipole strength is
where
becoming
along the real ![]() $\varOmega$ axis. The added mass coefficients are given in table 1 for the spheroid and its particular cases: the sphere (
$\varOmega$ axis. The added mass coefficients are given in table 1 for the spheroid and its particular cases: the sphere (![]() $\epsilon = 1$), the horizontal disc (
$\epsilon = 1$), the horizontal disc (![]() $\epsilon = 0$) and the vertical needle (
$\epsilon = 0$) and the vertical needle (![]() $\epsilon = \infty$).
$\epsilon = \infty$).
The particular results from the literature are all recovered. As ![]() $\varOmega \to \infty$, the inertial coefficients of the cylinder and the spheroid in a homogeneous fluid are also recovered. They are denoted as
$\varOmega \to \infty$, the inertial coefficients of the cylinder and the spheroid in a homogeneous fluid are also recovered. They are denoted as ![]() $C_x^\infty$ and
$C_x^\infty$ and ![]() $C_z^\infty$ and involve
$C_z^\infty$ and involve
for the spheroid, becoming ![]() $D(1) = 1/3$ for the sphere.
$D(1) = 1/3$ for the sphere.
The frequency variations of added mass are plotted in figures 3 and 4. They are consistent with the measurements by Ermanyuk (Reference Ermanyuk2000), Ermanyuk & Gavrilov (Reference Ermanyuk and Gavrilov2002a) and Brouzet et al. (Reference Brouzet, Ermanyuk, Moulin, Pillet and Dauxois2017) for a circular cylinder, Ermanyuk (Reference Ermanyuk2002) and Ermanyuk & Gavrilov (Reference Ermanyuk and Gavrilov2003) for a sphere and Ermanyuk (Reference Ermanyuk2002) for oblate and prolate spheroids, all for horizontal oscillations. Wave damping is only observed in the frequency range ![]() $|\varOmega | < 1$ of propagating waves, and vanishes at
$|\varOmega | < 1$ of propagating waves, and vanishes at ![]() $|\varOmega | > 1$ for evanescent waves. For the cylinder, there is no inertial added mass in the propagating case, but the same is not true for the spheroid. The damping coefficient does not vanish at zero frequency for the cylinder, while the inertial coefficient diverges logarithmically for the vertical motion of the spheroid. These remarks will have implications when formulating the Kramers–Kronig relations in § 6.1.
$|\varOmega | > 1$ for evanescent waves. For the cylinder, there is no inertial added mass in the propagating case, but the same is not true for the spheroid. The damping coefficient does not vanish at zero frequency for the cylinder, while the inertial coefficient diverges logarithmically for the vertical motion of the spheroid. These remarks will have implications when formulating the Kramers–Kronig relations in § 6.1.

Figure 3. Frequency variations of (a,c) the inertial coefficients ![]() $\mathrm {Re}\ C_x(\omega )$ and
$\mathrm {Re}\ C_x(\omega )$ and ![]() $\mathrm {Re}\ C_z(\omega )$ and (b,d) the damping coefficients
$\mathrm {Re}\ C_z(\omega )$ and (b,d) the damping coefficients ![]() $\varOmega\ \mathrm {Im}\ C_x(\omega )$ and
$\varOmega\ \mathrm {Im}\ C_x(\omega )$ and ![]() $\varOmega\ \mathrm {Im}\ C_z(\omega )$ of an elliptic cylinder of aspect ratio
$\varOmega\ \mathrm {Im}\ C_z(\omega )$ of an elliptic cylinder of aspect ratio ![]() $\epsilon$ oscillating (a,b) horizontally or (c,d) vertically.
$\epsilon$ oscillating (a,b) horizontally or (c,d) vertically.

Figure 4. Same as figure 3 for a spheroid.
5.2. Energy radiation
An important manifestation of internal waves in the ocean is the so-called internal or baroclinic tide, generated by the ebb and flow of the barotropic tide over bottom topography (Garrett & Kunze Reference Garrett and Kunze2007) or at the continental slope (Baines Reference Baines1982). Together with wind-generated waves at the surface, and lee waves generated by the flow of ocean currents over bottom topography, the internal tide is now thought to play an essential part in the mixing of the ocean (Ferrari & Wunsch Reference Ferrari and Wunsch2009; Ferrari Reference Ferrari2014; Ferrari et al. Reference Ferrari, Mashayek, McDougall, Nikurashin and Campin2016; MacKinnon et al. Reference MacKinnon2017; Sarkar & Scotti Reference Sarkar and Scotti2017; Whalen et al. Reference Whalen, de Lavergne, Naveira Garabato, Klymak, MacKinnon and Sheen2020; Legg Reference Legg2021). For small tidal excursion, namely small amplitude of the barotropic tidal motion compared with the width of the topography, the problem is linear and equivalent to the oscillation of the topography in an ocean at rest. In this context, the average wave power ![]() $\langle P\rangle$ represents the rate at which barotropic energy is converted to baroclinic form; hence, the name, sometimes used, of ‘conversion rate’ (Llewellyn Smith & Young Reference Llewellyn Smith and Young2002). For a recent study of its calculation in a general setting and an up-to-date bibliography, see Papoutsellis, Mercier & Grisouard (Reference Papoutsellis, Mercier and Grisouard2023).
$\langle P\rangle$ represents the rate at which barotropic energy is converted to baroclinic form; hence, the name, sometimes used, of ‘conversion rate’ (Llewellyn Smith & Young Reference Llewellyn Smith and Young2002). For a recent study of its calculation in a general setting and an up-to-date bibliography, see Papoutsellis, Mercier & Grisouard (Reference Papoutsellis, Mercier and Grisouard2023).
Topographies are called subcritical or supercritical depending on whether their maximum slope is smaller or larger than the slope of the wave rays, respectively, inclined at the angle ![]() $\arcsin \varOmega$ to the horizontal. The waves radiated by supercritical topography take the form of critical beams tangential to the topography; these are thinner than the beams from subcritical topography, hence, are more prone to breaking and mixing. See Machicoane et al. (Reference Machicoane, Cortet, Voisin and Moisy2015) and Le Dizès & Le Bars (Reference Le Dizès and Le Bars2017) for discussions of critical beams in the context of inertial waves. The semi-elliptic ridge and the hemispheroidal seamount, which are the oceanic analogues of the elliptic cylinder and the spheroid, are unconditionally supercritical, irrespective of the tidal frequency. Their experimental or numerical studies include Zhang, King & Swinney (Reference Zhang, King and Swinney2007) for a semi-circular ridge, King, Zhang & Swinney (Reference King, Zhang and Swinney2009) and Voisin, Ermanyuk & Flór (Reference Voisin, Ermanyuk and Flór2011) for a hemispherical seamount and Shmakova, Ermanyuk & Flór (Reference Shmakova, Ermanyuk and Flór2017) for a semi-ellipsoidal seamount.
$\arcsin \varOmega$ to the horizontal. The waves radiated by supercritical topography take the form of critical beams tangential to the topography; these are thinner than the beams from subcritical topography, hence, are more prone to breaking and mixing. See Machicoane et al. (Reference Machicoane, Cortet, Voisin and Moisy2015) and Le Dizès & Le Bars (Reference Le Dizès and Le Bars2017) for discussions of critical beams in the context of inertial waves. The semi-elliptic ridge and the hemispheroidal seamount, which are the oceanic analogues of the elliptic cylinder and the spheroid, are unconditionally supercritical, irrespective of the tidal frequency. Their experimental or numerical studies include Zhang, King & Swinney (Reference Zhang, King and Swinney2007) for a semi-circular ridge, King, Zhang & Swinney (Reference King, Zhang and Swinney2009) and Voisin, Ermanyuk & Flór (Reference Voisin, Ermanyuk and Flór2011) for a hemispherical seamount and Shmakova, Ermanyuk & Flór (Reference Shmakova, Ermanyuk and Flór2017) for a semi-ellipsoidal seamount.
Energy radiation takes place entirely in the frequency range ![]() $|\varOmega | < 1$ of propagating waves. Using (4.33), we obtain, for the cylinder,
$|\varOmega | < 1$ of propagating waves. Using (4.33), we obtain, for the cylinder,
and, for the spheroid,
 \begin{equation} \langle P\rangle = \frac{{\rm \pi}^2}{3}\rho_{00}Nab^2 \frac{(1-\varOmega^2)^{1/2}} {\displaystyle (1+|\varUpsilon|^2)^{3/2}} \left[ \frac{2U^2}{|1+D(\varUpsilon)|^2}+ \left(\frac{1}{\varOmega^2}-1\right) \frac{W^2}{|1-D(\varUpsilon)|^2} \right]. \end{equation}
\begin{equation} \langle P\rangle = \frac{{\rm \pi}^2}{3}\rho_{00}Nab^2 \frac{(1-\varOmega^2)^{1/2}} {\displaystyle (1+|\varUpsilon|^2)^{3/2}} \left[ \frac{2U^2}{|1+D(\varUpsilon)|^2}+ \left(\frac{1}{\varOmega^2}-1\right) \frac{W^2}{|1-D(\varUpsilon)|^2} \right]. \end{equation}
The variations of the wave power with ![]() $\varOmega$ are plotted in figure 5 for fixed excursion
$\varOmega$ are plotted in figure 5 for fixed excursion ![]() $A$ and varying angle
$A$ and varying angle ![]() $\alpha$ of oscillation to the horizontal, such that
$\alpha$ of oscillation to the horizontal, such that ![]() $(U,W) = NA\varOmega (\cos \alpha,\sin \alpha )$. The power is normalized by
$(U,W) = NA\varOmega (\cos \alpha,\sin \alpha )$. The power is normalized by ![]() $P_0 = {\rm \pi}\rho _{00}N^3abA^2$ for the cylinder and
$P_0 = {\rm \pi}\rho _{00}N^3abA^2$ for the cylinder and ![]() $(4/3){\rm \pi} \rho _{00}N^3a^2bA^2$ for the spheroid. It is a maximum at
$(4/3){\rm \pi} \rho _{00}N^3a^2bA^2$ for the spheroid. It is a maximum at ![]() $\varOmega _{m} = (2/3)^{1/2} \approx 0.816$ independent of
$\varOmega _{m} = (2/3)^{1/2} \approx 0.816$ independent of ![]() $\alpha$ and
$\alpha$ and ![]() $\epsilon$ for the cylinder, corresponding to propagation at
$\epsilon$ for the cylinder, corresponding to propagation at ![]() $35\,^\circ$ to the vertical, and
$35\,^\circ$ to the vertical, and ![]() $0.816 < \varOmega _{m} < 1$ for the spheroid, dependent on
$0.816 < \varOmega _{m} < 1$ for the spheroid, dependent on ![]() $\alpha$ and
$\alpha$ and ![]() $\epsilon$, as shown in figure 6. For the sphere,
$\epsilon$, as shown in figure 6. For the sphere, ![]() $\varOmega _{m}$ varies between
$\varOmega _{m}$ varies between ![]() $0.846$ for
$0.846$ for ![]() $\alpha = 0$ and
$\alpha = 0$ and ![]() $0.835$ for
$0.835$ for ![]() $\alpha = {\rm \pi}/2$.
$\alpha = {\rm \pi}/2$.

Figure 5. Frequency variations of the power outputs of (a,c,e,g,i) elliptic cylinders and (b,d,f,h,j) spheroids of aspect ratios (a,b) ![]() $\epsilon = 0.2$, (c,d)
$\epsilon = 0.2$, (c,d) ![]() $\epsilon = 0.5$, (e,f)
$\epsilon = 0.5$, (e,f) ![]() $\epsilon = 1$, (g,h)
$\epsilon = 1$, (g,h) ![]() $\epsilon = 2$ and (i,j)
$\epsilon = 2$ and (i,j) ![]() $\epsilon = 5$ oscillating with fixed excursion at the angle
$\epsilon = 5$ oscillating with fixed excursion at the angle ![]() $\alpha$ to the horizontal.
$\alpha$ to the horizontal.

Figure 6. Frequency ![]() $\varOmega _{m}$ of maximum power output of a spheroid of aspect ratio
$\varOmega _{m}$ of maximum power output of a spheroid of aspect ratio ![]() $\epsilon$ oscillating with fixed excursion at the angle
$\epsilon$ oscillating with fixed excursion at the angle ![]() $\alpha$ to the horizontal.
$\alpha$ to the horizontal.
In the laboratory, when the waves are generated by an oscillating body, the excursion is usually set by practical constraints, and the frequency ratio ![]() $\varOmega$ is chosen as close as possible to
$\varOmega$ is chosen as close as possible to ![]() $0.8$ in order to maximize wave radiation for that excursion, or
$0.8$ in order to maximize wave radiation for that excursion, or ![]() $0.8/n$ when the generation of an
$0.8/n$ when the generation of an ![]() $n$th harmonic is looked for (Shmakova et al. Reference Shmakova, Ermanyuk and Flór2017). In circumstances where the waves were generated by a broadband disturbance, such as the collapse of a mixed region (Wu Reference Wu1969) or a buoyant fluid parcel (Cerasoli Reference Cerasoli1978), both two-dimensional, or the decay of a three-dimensional turbulent region (Riley, Metcalfe & Weissman Reference Riley, Metcalfe and Weissman1981), a well-defined peak has been observed in the wave spectrum at
$n$th harmonic is looked for (Shmakova et al. Reference Shmakova, Ermanyuk and Flór2017). In circumstances where the waves were generated by a broadband disturbance, such as the collapse of a mixed region (Wu Reference Wu1969) or a buoyant fluid parcel (Cerasoli Reference Cerasoli1978), both two-dimensional, or the decay of a three-dimensional turbulent region (Riley, Metcalfe & Weissman Reference Riley, Metcalfe and Weissman1981), a well-defined peak has been observed in the wave spectrum at ![]() $\varOmega _{m} = 0.8$,
$\varOmega _{m} = 0.8$, ![]() $0.7$ and
$0.7$ and ![]() $0.5$, respectively. If the disturbance can be viewed as an assembly of turbulent patches oscillating with random frequencies in random directions with an approximately constant excursion, then the above mechanism might explain the emergence of a well-defined peak.
$0.5$, respectively. If the disturbance can be viewed as an assembly of turbulent patches oscillating with random frequencies in random directions with an approximately constant excursion, then the above mechanism might explain the emergence of a well-defined peak.
6. Time-dependent aspects
At its core, added mass is a generalized susceptibility expressing the non-local temporal linear relation between a cause – the velocity ![]() $\boldsymbol {U}(t)$ of the moving body – and its effect – the hydrodynamic force
$\boldsymbol {U}(t)$ of the moving body – and its effect – the hydrodynamic force ![]() $\boldsymbol {F}(t)$ – through the convolution integral (4.8); see Landau & Lifshitz (Reference Landau and Lifshitz1980, § 123) for a presentation of generalized susceptibilities, and Landau & Lifshitz (Reference Landau and Lifshitz1984, §§ 77 and 82) and Jackson (Reference Jackson1999, § 7.10) for the particular case of the electric permittivity. We investigate the consequences of that integral in this section.
$\boldsymbol {F}(t)$ – through the convolution integral (4.8); see Landau & Lifshitz (Reference Landau and Lifshitz1980, § 123) for a presentation of generalized susceptibilities, and Landau & Lifshitz (Reference Landau and Lifshitz1984, §§ 77 and 82) and Jackson (Reference Jackson1999, § 7.10) for the particular case of the electric permittivity. We investigate the consequences of that integral in this section.
6.1. Kramers–Kronig relations
First comes causality, namely the fact that effect cannot precede cause. In time this means ![]() $m_{ij}(t) = 0$ for
$m_{ij}(t) = 0$ for ![]() $t < 0$, and in frequency the analyticity of
$t < 0$, and in frequency the analyticity of ![]() $m_{ij}(\omega )$ in the upper half of the complex
$m_{ij}(\omega )$ in the upper half of the complex ![]() $\omega$ plane. A variety of properties of
$\omega$ plane. A variety of properties of ![]() $m_{ij}(\omega )$ follow from this, discussed by Landau & Lifshitz (Reference Landau and Lifshitz1980, § 123) and Jackson (Reference Jackson1999, § 7.10). We adapt here their conclusions to the problem at hand.
$m_{ij}(\omega )$ follow from this, discussed by Landau & Lifshitz (Reference Landau and Lifshitz1980, § 123) and Jackson (Reference Jackson1999, § 7.10). We adapt here their conclusions to the problem at hand.
Real values of ![]() $m_{ij}(\omega )$ are obtained on the evanescent part of the real frequency axis, where
$m_{ij}(\omega )$ are obtained on the evanescent part of the real frequency axis, where ![]() $m_{ij}(\omega )$ increases from
$m_{ij}(\omega )$ increases from ![]() $0$ to
$0$ to ![]() $m_{ij}^\infty$ as
$m_{ij}^\infty$ as ![]() $\omega$ varies from
$\omega$ varies from ![]() $N$ to
$N$ to ![]() $+\infty$ (or
$+\infty$ (or ![]() $-N$ to
$-N$ to ![]() $-\infty$), and on the positive imaginary axis, where
$-\infty$), and on the positive imaginary axis, where ![]() $m_{ij}(\omega )$ increases from
$m_{ij}(\omega )$ increases from ![]() $m_{ij}^\infty$ to
$m_{ij}^\infty$ to ![]() $+\infty$ as
$+\infty$ as ![]() $\omega$ varies from
$\omega$ varies from ![]() $\mathrm {i}\infty$ to
$\mathrm {i}\infty$ to ![]() $\mathrm {i}0$. At infinity along any direction of the upper half-plane, we have
$\mathrm {i}0$. At infinity along any direction of the upper half-plane, we have
namely the oscillations are so fast that buoyancy cannot manifest itself and added mass takes its value in a homogeneous fluid. At the origin, decomposing ![]() $m_{ij}(\omega )$ into its real part
$m_{ij}(\omega )$ into its real part ![]() $\mu _{ij}(\omega )$ and its imaginary part
$\mu _{ij}(\omega )$ and its imaginary part ![]() $\lambda _{ij}(\omega )/\omega$, we see from § 5.1 that
$\lambda _{ij}(\omega )/\omega$, we see from § 5.1 that ![]() $\lambda _{ij}(\omega )$ may be non-zero, yielding a first-order pole, and that
$\lambda _{ij}(\omega )$ may be non-zero, yielding a first-order pole, and that ![]() $\mu _{ij}(\omega )$ may exhibit a logarithmic singularity.
$\mu _{ij}(\omega )$ may exhibit a logarithmic singularity.
For real ![]() $\omega$, we integrate
$\omega$, we integrate ![]() $[m_{ij}(\omega ')-m_{ij}^\infty ]/(\omega '-\omega )$ in the
$[m_{ij}(\omega ')-m_{ij}^\infty ]/(\omega '-\omega )$ in the ![]() $\omega '$ plane along the contour shown in figure 7. The contribution of the large semi-circle at infinity vanishes by (6.1). The small semi-circles at the poles
$\omega '$ plane along the contour shown in figure 7. The contribution of the large semi-circle at infinity vanishes by (6.1). The small semi-circles at the poles ![]() $\omega ' = 0$ and
$\omega ' = 0$ and ![]() $\omega ' = \omega$ give residue contributions, to which the logarithmic divergence of
$\omega ' = \omega$ give residue contributions, to which the logarithmic divergence of ![]() $\mu _{ij}(\omega )$ at
$\mu _{ij}(\omega )$ at ![]() $\omega ' = 0$ is too weak to contribute. We obtain
$\omega ' = 0$ is too weak to contribute. We obtain
where the stroke through the integral denotes a principal value. Separating real and imaginary parts, we have
or, taking into account that ![]() $\mu _{ij}(\omega )$ and
$\mu _{ij}(\omega )$ and ![]() $\lambda _{ij}(\omega )$ are even functions of
$\lambda _{ij}(\omega )$ are even functions of ![]() $\omega$,
$\omega$,
This is the most general form of the Kramers–Kronig relations for internal waves, expressing ![]() $\mu _{ij}(\omega )$ for real frequencies in terms of
$\mu _{ij}(\omega )$ for real frequencies in terms of ![]() $\lambda _{ij}(\omega )$ also for real frequencies, and vice versa. They were verified analytically by Ermanyuk & Gavrilov (Reference Ermanyuk and Gavrilov2002a) for a circular cylinder, using added mass coefficients deduced from Hurley (Reference Hurley1997).
$\lambda _{ij}(\omega )$ also for real frequencies, and vice versa. They were verified analytically by Ermanyuk & Gavrilov (Reference Ermanyuk and Gavrilov2002a) for a circular cylinder, using added mass coefficients deduced from Hurley (Reference Hurley1997).

Figure 7. Contour for the derivation of the Kramers–Kronig relations.
Relation (6.4a) may be of practical interest, as it provides a way of calculating the inertial coefficient ![]() $\mu _{ij}(\omega )$ at any real frequency, should the variations of the damping coefficient
$\mu _{ij}(\omega )$ at any real frequency, should the variations of the damping coefficient ![]() $\lambda _{ij}(\omega )$ be known exactly or determined empirically, by (4.33), from measurements of the wave power
$\lambda _{ij}(\omega )$ be known exactly or determined empirically, by (4.33), from measurements of the wave power ![]() $\langle P\rangle$. Together, (6.4a)–(6.4b) may be used to deduce connections between the behaviours of the coefficients at low, intermediate and high frequencies, transferring the burden of calculating these coefficients onto the frequency range in which the calculation is easiest, as pointed out for surface gravity waves by Greenhow (Reference Greenhow1984, Reference Greenhow1986), based on Kotik & Mangulis (Reference Kotik and Mangulis1962).
$\langle P\rangle$. Together, (6.4a)–(6.4b) may be used to deduce connections between the behaviours of the coefficients at low, intermediate and high frequencies, transferring the burden of calculating these coefficients onto the frequency range in which the calculation is easiest, as pointed out for surface gravity waves by Greenhow (Reference Greenhow1984, Reference Greenhow1986), based on Kotik & Mangulis (Reference Kotik and Mangulis1962).
6.2. Memory effect
Physically, added mass may be decomposed into two parts: an instantaneous response with no effect of the stratification, and a delayed response caused by internal wave radiation. We write
where
so that the hydrodynamic force (4.8) becomes
Accordingly, the effect of the stratification on added mass may be characterized as a memory effect, interpreted by Newman (Reference Newman2017, § 6.19), for surface gravity waves, as the feedback that the pressure fluctuations in the waves, once generated by the body, will continue to have on this body as they propagate away, for all subsequent times.
The memory kernel ![]() $m_{ij}^{M}(t)$, or impulse response function (Cummins Reference Cummins1962; Ogilvie Reference Ogilvie1964), may be expressed as the coefficient
$m_{ij}^{M}(t)$, or impulse response function (Cummins Reference Cummins1962; Ogilvie Reference Ogilvie1964), may be expressed as the coefficient
It is a real causal function, ![]() $f(t)$ say, and as such may be written in terms of the real part of its Fourier transform
$f(t)$ say, and as such may be written in terms of the real part of its Fourier transform ![]() $f(\omega )$ alone, or the imaginary part alone, as
$f(\omega )$ alone, or the imaginary part alone, as
Account has been taken of the fact that the imaginary part, proportional to the damping coefficient ![]() $\lambda _{ij}(\omega )$, is non-zero only over the propagating frequency range
$\lambda _{ij}(\omega )$, is non-zero only over the propagating frequency range ![]() $|\omega | < N$.
$|\omega | < N$.
Changing variable according to ![]() $\omega = N\cos \theta$, we obtain, for the elliptic cylinder,
$\omega = N\cos \theta$, we obtain, for the elliptic cylinder,
where
or alternatively, in terms of the Bessel functions ![]() $\mathrm {J}_n(t)$,
$\mathrm {J}_n(t)$,
Using (10.22.2) from Olver et al. (Reference Olver, Lozier, Boisvert and Clark2010), we have
where ![]() $\boldsymbol {H}_n(t)$ denotes a Struve function. The variations of the kernel are the same for horizontal and vertical motions. They are plotted in figure 8 where time is normalized by the buoyancy period
$\boldsymbol {H}_n(t)$ denotes a Struve function. The variations of the kernel are the same for horizontal and vertical motions. They are plotted in figure 8 where time is normalized by the buoyancy period ![]() $T = 2{\rm \pi} /N$.
$T = 2{\rm \pi} /N$.

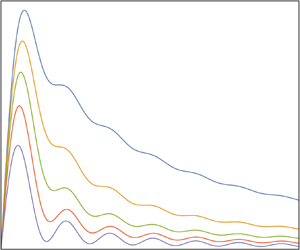
Figure 8. Exact (solid line) and asymptotic (dashed line) variations of the memory kernel for the translation of an elliptic cylinder.
Their interpretation is made easier by the expansion of the kernel for large time ![]() $Nt \gg 1$. Lighthill (Reference Lighthill1958, chapter 4) showed that the asymptotic behaviour of a Fourier transform follows from expanding the original function near the points where it, or any of its successive derivatives, is singular, then transforming these expansions and adding the results. The same applies to an inverse transform such as (6.8). The singularities are a pole at
$Nt \gg 1$. Lighthill (Reference Lighthill1958, chapter 4) showed that the asymptotic behaviour of a Fourier transform follows from expanding the original function near the points where it, or any of its successive derivatives, is singular, then transforming these expansions and adding the results. The same applies to an inverse transform such as (6.8). The singularities are a pole at ![]() $\omega = 0$ and two branch points at
$\omega = 0$ and two branch points at ![]() $\omega = \pm N$. Their contributions are evaluated using table 4 of Voisin (Reference Voisin2003), to give
$\omega = \pm N$. Their contributions are evaluated using table 4 of Voisin (Reference Voisin2003), to give
 \begin{equation} C^{M}(t) \sim 1-\left(\frac{2}{\rm \pi}\right)^{1/2} \frac{\cos(Nt-{\rm \pi}/4)}{(Nt)^{3/2}}. \end{equation}
\begin{equation} C^{M}(t) \sim 1-\left(\frac{2}{\rm \pi}\right)^{1/2} \frac{\cos(Nt-{\rm \pi}/4)}{(Nt)^{3/2}}. \end{equation}
This expansion, shown in figure 8, is seen to hold for almost any value of ![]() $Nt$. The kernel thus superposes buoyancy oscillations of frequency
$Nt$. The kernel thus superposes buoyancy oscillations of frequency ![]() $N$ and amplitude decaying as
$N$ and amplitude decaying as ![]() $t^{-3/2}$, faster than the decay as
$t^{-3/2}$, faster than the decay as ![]() $t^{-1/2}$ of the kernel of the Basset–Boussinesq memory integral (Boussinesq Reference Boussinesq1885; Basset Reference Basset1888), to a constant value. Accordingly, however much time has passed, the force exerted on the cylinder remains affected by the full past history of its motion. This feature is specific to two dimensions.
$t^{-1/2}$ of the kernel of the Basset–Boussinesq memory integral (Boussinesq Reference Boussinesq1885; Basset Reference Basset1888), to a constant value. Accordingly, however much time has passed, the force exerted on the cylinder remains affected by the full past history of its motion. This feature is specific to two dimensions.
For the spheroid, we have
 \begin{align} C_x^{M}(t) & = 2\frac{H(t)}{\epsilon} \int_0^{{\rm \pi}/2} \sin(Nt\cos\theta) \cos\theta (1+\epsilon^2\tan^2\theta)^{3/2} \nonumber\\ & \quad \times \biggl\{ \frac{{\rm \pi}^2}{4}+ \left[ \operatorname{arcsinh}(\epsilon\tan\theta)- \frac{2+\epsilon^2\tan^2\theta}{\epsilon\tan\theta} (1+\epsilon^2\tan^2\theta)^{1/2} \right]^2 \biggr\}^{{-}1} \,\mathrm{d}\theta, \end{align}
\begin{align} C_x^{M}(t) & = 2\frac{H(t)}{\epsilon} \int_0^{{\rm \pi}/2} \sin(Nt\cos\theta) \cos\theta (1+\epsilon^2\tan^2\theta)^{3/2} \nonumber\\ & \quad \times \biggl\{ \frac{{\rm \pi}^2}{4}+ \left[ \operatorname{arcsinh}(\epsilon\tan\theta)- \frac{2+\epsilon^2\tan^2\theta}{\epsilon\tan\theta} (1+\epsilon^2\tan^2\theta)^{1/2} \right]^2 \biggr\}^{{-}1} \,\mathrm{d}\theta, \end{align} \begin{align} C_z^{M}(t) & = \frac{H(t)}{\epsilon} \int_0^{{\rm \pi}/2} \sin(Nt\cos\theta) \frac{\sin^2\theta}{\cos\theta} (1+\epsilon^2\tan^2\theta)^{3/2} \nonumber\\& \quad \times \left\{ \frac{{\rm \pi}^2}{4}+ [\operatorname{arcsinh}(\epsilon\tan\theta)+ \epsilon\tan\theta(1+\epsilon^2\tan^2\theta)^{1/2}]^2 \right\}^{{-}1} \,\mathrm{d}\theta, \end{align}
\begin{align} C_z^{M}(t) & = \frac{H(t)}{\epsilon} \int_0^{{\rm \pi}/2} \sin(Nt\cos\theta) \frac{\sin^2\theta}{\cos\theta} (1+\epsilon^2\tan^2\theta)^{3/2} \nonumber\\& \quad \times \left\{ \frac{{\rm \pi}^2}{4}+ [\operatorname{arcsinh}(\epsilon\tan\theta)+ \epsilon\tan\theta(1+\epsilon^2\tan^2\theta)^{1/2}]^2 \right\}^{{-}1} \,\mathrm{d}\theta, \end{align}
namely different variations for horizontal and vertical motions, which cannot be expressed in terms of known functions. They are plotted in figure 9 and take the form of decaying buoyancy oscillations at the frequency ![]() $N$, superposed to a monotonous decrease for vertical motion and a slow non-monotonous variation for horizontal motion.
$N$, superposed to a monotonous decrease for vertical motion and a slow non-monotonous variation for horizontal motion.

Figure 9. Exact (solid line) and asymptotic (dashed line) variations of the memory kernel for the (a,c,e,g,i) horizontal and (b,d,f,h,j) vertical translations of spheroids of aspect ratios (a,b) ![]() $\epsilon = 0.2$, (c,d)
$\epsilon = 0.2$, (c,d) ![]() $\epsilon = 0.5$, (e,f)
$\epsilon = 0.5$, (e,f) ![]() $\epsilon = 1$, (g,h)
$\epsilon = 1$, (g,h) ![]() $\epsilon = 2$ and (i,j)
$\epsilon = 2$ and (i,j) ![]() $\epsilon = 5$.
$\epsilon = 5$.
Lighthill's (Reference Lighthill1958) asymptotic approach, used for the cylinder, considers only real values of the original and transformed variables, and hence, can only give algebraic decays with or without oscillations. These are indeed the behaviours observed for very large ![]() $Nt$ in all circumstances, but not, for moderately large
$Nt$ in all circumstances, but not, for moderately large ![]() $Nt$, the behaviour observed in figure 9 for horizontal motion. A generalization of the approach is in order, taking complex singularities into account and evaluating their contributions as contour integrals gathered in Appendix C. The best outcome, encompassing the cylinder as a particular case, is obtained by considering the singularities at which either the modulus of the transform diverges, or a branch cut starts across which this modulus undergoes a jump.
$Nt$, the behaviour observed in figure 9 for horizontal motion. A generalization of the approach is in order, taking complex singularities into account and evaluating their contributions as contour integrals gathered in Appendix C. The best outcome, encompassing the cylinder as a particular case, is obtained by considering the singularities at which either the modulus of the transform diverges, or a branch cut starts across which this modulus undergoes a jump.
The singularities of ![]() $C_x(\omega )$ and
$C_x(\omega )$ and ![]() $C_z(\omega )$ are linked to those of
$C_z(\omega )$ are linked to those of ![]() $D(\varUpsilon )$, whose variations are shown in figure 10. The only singularity is a branch point at
$D(\varUpsilon )$, whose variations are shown in figure 10. The only singularity is a branch point at ![]() $\varUpsilon = -1$, with a cut along the negative real axis. In the plane of the complex variable
$\varUpsilon = -1$, with a cut along the negative real axis. In the plane of the complex variable ![]() $\omega$, scaled as
$\omega$, scaled as ![]() $\varOmega = \omega /N$, to which
$\varOmega = \omega /N$, to which ![]() $\varUpsilon$ is related by (5.4), three or four singularities are observed depending on the parameter
$\varUpsilon$ is related by (5.4), three or four singularities are observed depending on the parameter ![]() $\epsilon$: two singularities at
$\epsilon$: two singularities at ![]() $\varOmega = \pm 1$, corresponding to
$\varOmega = \pm 1$, corresponding to ![]() $\varUpsilon = 0$, in the vicinity of which
$\varUpsilon = 0$, in the vicinity of which
 \begin{equation} D(\varUpsilon) \sim 1-\frac{\rm \pi}{2}\varUpsilon \sim 1-{\rm \pi}\epsilon \biggl[ \left(\frac{\varOmega-1}{2}\right)^{1/2}, \mathrm{i}\left(\frac{\varOmega+1}{2}\right)^{1/2} \biggr], \end{equation}
\begin{equation} D(\varUpsilon) \sim 1-\frac{\rm \pi}{2}\varUpsilon \sim 1-{\rm \pi}\epsilon \biggl[ \left(\frac{\varOmega-1}{2}\right)^{1/2}, \mathrm{i}\left(\frac{\varOmega+1}{2}\right)^{1/2} \biggr], \end{equation}
yielding an algebraically decaying oscillation at the buoyancy frequency; one singularity at ![]() $\varOmega = 0$, corresponding to
$\varOmega = 0$, corresponding to ![]() $\varUpsilon \to \infty$, in the vicinity of which
$\varUpsilon \to \infty$, in the vicinity of which
yielding an aperiodic algebraic decay; and when ![]() $\epsilon < 1$, a singularity at
$\epsilon < 1$, a singularity at ![]() $\varOmega = -\mathrm {i}\varOmega _{s}$ with
$\varOmega = -\mathrm {i}\varOmega _{s}$ with
corresponding to ![]() $\varUpsilon \to -1$, in the vicinity of which
$\varUpsilon \to -1$, in the vicinity of which
yielding an aperiodic exponential decay. The branch cut away from ![]() $\varOmega = 0$ stretches along the whole negative imaginary axis when
$\varOmega = 0$ stretches along the whole negative imaginary axis when ![]() $\epsilon > 1$, and stops at
$\epsilon > 1$, and stops at ![]() $-\mathrm {i}\varOmega _{s}$ when
$-\mathrm {i}\varOmega _{s}$ when ![]() $\epsilon < 1$.
$\epsilon < 1$.

Figure 10. Variations of ![]() $D(\varUpsilon )$ in the complex
$D(\varUpsilon )$ in the complex ![]() $\varUpsilon$ plane. The surface height is set by the modulus of
$\varUpsilon$ plane. The surface height is set by the modulus of ![]() $D(\varUpsilon )$ and the colour by its argument. The solid lines represent the images of the real and imaginary axes.
$D(\varUpsilon )$ and the colour by its argument. The solid lines represent the images of the real and imaginary axes.
Typical variations of ![]() $C_x(\omega )$ and
$C_x(\omega )$ and ![]() $C_z(\omega )$ are shown in figure 11. For vertical motion, the relevant singularities are
$C_z(\omega )$ are shown in figure 11. For vertical motion, the relevant singularities are ![]() $\varOmega = 0$ and
$\varOmega = 0$ and ![]() $\varOmega = \pm 1$. Using (C1), (C2) and (C4), we obtain
$\varOmega = \pm 1$. Using (C1), (C2) and (C4), we obtain
 \begin{equation} C_z^{M}(t) \sim \frac{1-H(1-\epsilon)\exp(-\omega_{s}t)}{\epsilon^2Nt} - \left(\frac{2}{\rm \pi}\right)^{3/2} \frac{\cos(Nt-{\rm \pi}/4)} {\epsilon(Nt)^{3/2}}, \end{equation}
\begin{equation} C_z^{M}(t) \sim \frac{1-H(1-\epsilon)\exp(-\omega_{s}t)}{\epsilon^2Nt} - \left(\frac{2}{\rm \pi}\right)^{3/2} \frac{\cos(Nt-{\rm \pi}/4)} {\epsilon(Nt)^{3/2}}, \end{equation}
namely buoyancy oscillations of frequency ![]() $N$ and amplitude decay as
$N$ and amplitude decay as ![]() $t^{-3/2}$, superposed to an aperiodic decay as
$t^{-3/2}$, superposed to an aperiodic decay as ![]() $t^{-1}$, with
$t^{-1}$, with ![]() $\omega _{s} = N\varOmega _{s}$.
$\omega _{s} = N\varOmega _{s}$.

Figure 11. Variations of (a–c) ![]() $C_x(\omega )$ in the complex
$C_x(\omega )$ in the complex ![]() $\varOmega$ plane for the horizontal translation of spheroids, and (d–f)
$\varOmega$ plane for the horizontal translation of spheroids, and (d–f) ![]() $C_z(\omega )$ for their vertical translation. The spheroids have aspect ratios (a,d)
$C_z(\omega )$ for their vertical translation. The spheroids have aspect ratios (a,d) ![]() $\epsilon = 0.5$, (b,e)
$\epsilon = 0.5$, (b,e) ![]() $\epsilon = 1$ and (c,f)
$\epsilon = 1$ and (c,f) ![]() $\epsilon = 2$.
$\epsilon = 2$.
For horizontal motion, the singularity ![]() $\varOmega = 0$ is no longer relevant but new ones come into play, associated with the complex conjugate solutions
$\varOmega = 0$ is no longer relevant but new ones come into play, associated with the complex conjugate solutions ![]() $\varUpsilon _{c}$ and
$\varUpsilon _{c}$ and ![]() $\overline {\varUpsilon _{c}}$ of
$\overline {\varUpsilon _{c}}$ of ![]() $D(\varUpsilon ) = -1$, where
$D(\varUpsilon ) = -1$, where
A new constraint arises, ![]() $|\mathrm {Re}\ \varOmega | < 1$ and
$|\mathrm {Re}\ \varOmega | < 1$ and ![]() $\mathrm {Im}\ \varOmega < 0$, namely the singularities must be situated in the lower half-plane between the two branch cuts away from
$\mathrm {Im}\ \varOmega < 0$, namely the singularities must be situated in the lower half-plane between the two branch cuts away from ![]() $\varOmega = \pm 1$, in order to belong to the proper Riemann sheet. This gives
$\varOmega = \pm 1$, in order to belong to the proper Riemann sheet. This gives ![]() $\epsilon < \epsilon _{c} \approx 2.396$ and leaves two poles
$\epsilon < \epsilon _{c} \approx 2.396$ and leaves two poles ![]() $\pm \varOmega _{r}-\mathrm {i}\varOmega _{i}$, symmetric with respect to the imaginary axis, where
$\pm \varOmega _{r}-\mathrm {i}\varOmega _{i}$, symmetric with respect to the imaginary axis, where
and the determination of the square root is chosen such that ![]() $0 < \varOmega _{r} < 1$ and
$0 < \varOmega _{r} < 1$ and ![]() $\varOmega _{i} > 0$. Figure 11 illustrates how the poles approach the cuts as
$\varOmega _{i} > 0$. Figure 11 illustrates how the poles approach the cuts as ![]() $\epsilon$ increases, eventually crossing them at
$\epsilon$ increases, eventually crossing them at ![]() $\epsilon = \epsilon _{c}$ then vanishing. Applying the residue theorem together with (C2), we obtain
$\epsilon = \epsilon _{c}$ then vanishing. Applying the residue theorem together with (C2), we obtain
namely buoyancy oscillations of frequency ![]() $N$ and amplitude decay as
$N$ and amplitude decay as ![]() $t^{-3/2}$, superposed for
$t^{-3/2}$, superposed for ![]() $\epsilon < \epsilon _{c}$ to oscillations of frequency
$\epsilon < \epsilon _{c}$ to oscillations of frequency ![]() $\omega _{r} = N\varOmega _{r}$ and damping rate
$\omega _{r} = N\varOmega _{r}$ and damping rate ![]() $\omega _{i} = N\varOmega _{i}$.
$\omega _{i} = N\varOmega _{i}$.
As a rule, for both horizontal and vertical motions, the importance of the memory integral in the total hydrodynamic force (6.7) is larger for small ![]() $\epsilon$, namely for bodies that are horizontally flat. In these circumstances, the recent history of the motion is dominant, with the memory kernel exhibiting a peak within the first half-period followed by exponential decay for horizontal motion and algebraic decay for vertical motion. As
$\epsilon$, namely for bodies that are horizontally flat. In these circumstances, the recent history of the motion is dominant, with the memory kernel exhibiting a peak within the first half-period followed by exponential decay for horizontal motion and algebraic decay for vertical motion. As ![]() $\epsilon$ increases and the body gets more elongated vertically, the decay happens faster, hence, the peak becomes more pronounced and buoyancy oscillations take on a more prominent role afterwards. At larger
$\epsilon$ increases and the body gets more elongated vertically, the decay happens faster, hence, the peak becomes more pronounced and buoyancy oscillations take on a more prominent role afterwards. At larger ![]() $\epsilon$ the original peak remains present for vertical motion but vanishes for horizontal motion, leaving only buoyancy oscillations.
$\epsilon$ the original peak remains present for vertical motion but vanishes for horizontal motion, leaving only buoyancy oscillations.
We note that ![]() $C_z^{M}(t)$ is always positive. Accordingly, the memory force always opposes vertical acceleration, dragging the body back as it speeds up and pushing it forward at it slows down. This is a manifestation of the inhibition of vertical motion by the stratification, complementary to the observation, both experimental and numerical, that buoyancy always induces a resistance to steady vertical motion (Magnaudet & Mercier Reference Magnaudet and Mercier2020). By contrast,
$C_z^{M}(t)$ is always positive. Accordingly, the memory force always opposes vertical acceleration, dragging the body back as it speeds up and pushing it forward at it slows down. This is a manifestation of the inhibition of vertical motion by the stratification, complementary to the observation, both experimental and numerical, that buoyancy always induces a resistance to steady vertical motion (Magnaudet & Mercier Reference Magnaudet and Mercier2020). By contrast, ![]() $C_x^{M}(t)$ is both positive and negative, yielding an alternation of phases where the acceleration of the body is either opposed or fostered.
$C_x^{M}(t)$ is both positive and negative, yielding an alternation of phases where the acceleration of the body is either opposed or fostered.
7. Conclusion
The concept of added mass has been generalized to stratified fluids, taking internal waves into account and assuming the fluid to be inviscid, the stratification uniform and the Boussinesq approximation valid. Added mass has been defined in § 4 for the translation of a rigid body, and its relation clarified with the hydrodynamic force on the body, the dipole strength of this body, and the energy and momentum of the fluid. Added mass has been calculated in § 5.1 for an elliptic cylinder of horizontal axis, typical of two-dimensional bodies, and a spheroid of vertical axis, typical of three-dimensional bodies, based on boundary integral representations of these bodies by Voisin (Reference Voisin2021). Added mass appears as a complex function of the oscillation frequency ![]() $\omega$. Its real part
$\omega$. Its real part ![]() $\mu _{ij}(\omega )$ is associated with inertia and its imaginary part
$\mu _{ij}(\omega )$ is associated with inertia and its imaginary part ![]() $\lambda _{ij}(\omega )/\omega$ with wave damping. The tensors
$\lambda _{ij}(\omega )/\omega$ with wave damping. The tensors ![]() $\mu _{ij}(\omega )$ and
$\mu _{ij}(\omega )$ and ![]() $\lambda _{ij}(\omega )$, where
$\lambda _{ij}(\omega )$, where ![]() $i = 3$ corresponds to the vertical direction, are both symmetric; in addition,
$i = 3$ corresponds to the vertical direction, are both symmetric; in addition, ![]() $\lambda _{ij}(\omega )$ is positive definite and vanishes outside the frequency range
$\lambda _{ij}(\omega )$ is positive definite and vanishes outside the frequency range ![]() $|\omega | < N$ of propagating waves, with
$|\omega | < N$ of propagating waves, with ![]() $N$ the buoyancy frequency. Because of causality,
$N$ the buoyancy frequency. Because of causality, ![]() $\mu _{ij}(\omega )$ and
$\mu _{ij}(\omega )$ and ![]() $\lambda _{ij}(\omega )$ satisfy Kramers–Kronig relations derived in § 6.1.
$\lambda _{ij}(\omega )$ satisfy Kramers–Kronig relations derived in § 6.1.
A first application of added mass is the wave power, considered in § 5.2. For the internal tide, namely internal waves generated in the ocean by the ebb and flow of the barotropic tide over bottom topography (Garrett & Kunze Reference Garrett and Kunze2007), this power determines the rate at which barotropic energy is converted to baroclinic form. For oscillations of fixed excursion, the radiated power is a maximum at ![]() $\omega /N$ about
$\omega /N$ about ![]() $0.8$, corresponding to radiation at
$0.8$, corresponding to radiation at ![]() $35^\circ$ to the vertical, independent of the direction of oscillation for the cylinder and weakly dependent on it for the spheroid. This might provide an explanation for the observation, sometimes made, experimentally and numerically, of a clear peak in the wave spectrum for broadband forcing mechanisms such as the collapse of a mixed region (Wu Reference Wu1969), penetrative convection (Cerasoli Reference Cerasoli1978) and turbulent decay (Riley et al. Reference Riley, Metcalfe and Weissman1981).
$35^\circ$ to the vertical, independent of the direction of oscillation for the cylinder and weakly dependent on it for the spheroid. This might provide an explanation for the observation, sometimes made, experimentally and numerically, of a clear peak in the wave spectrum for broadband forcing mechanisms such as the collapse of a mixed region (Wu Reference Wu1969), penetrative convection (Cerasoli Reference Cerasoli1978) and turbulent decay (Riley et al. Reference Riley, Metcalfe and Weissman1981).
Another application is the oscillations through which a buoyant body, displaced from its equilibrium position, goes back to it. These oscillations are considered in a companion paper (Voisin Reference Voisin2024) for three configurations: a float displaced from its neutral level then released; a Cartesian diver driven by variations of the hydrostatic pressure then released; and a pendulum with a buoyant body at its end, to which an impulse is applied. Comparison with experiment will be seen to require the inclusion of viscous dissipation.
In the temporal domain, the modifications brought to added mass by the stratification may be viewed as a new memory force, expressed in § 6.2 as a convolution integral. The kernel of this integral exhibits the same variations independent of the direction of motion for the cylinder, namely an oscillation at the buoyancy frequency with an amplitude decaying as ![]() $t^{-3/2}$, superposed to a positive constant. Accordingly, the full previous history of a two-dimensional body determines the force exerted on it at any subsequent instant. For the spheroid, the same oscillations are present, superposed to an algebraic decay as
$t^{-3/2}$, superposed to a positive constant. Accordingly, the full previous history of a two-dimensional body determines the force exerted on it at any subsequent instant. For the spheroid, the same oscillations are present, superposed to an algebraic decay as ![]() $t^{-1}$ for vertical motion and an exponentially damped oscillation for horizontal motion. The force always opposes the acceleration of the body for vertical motion, while for horizontal motion, the acceleration is alternatively opposed and fostered.
$t^{-1}$ for vertical motion and an exponentially damped oscillation for horizontal motion. The force always opposes the acceleration of the body for vertical motion, while for horizontal motion, the acceleration is alternatively opposed and fostered.
Added mass has been investigated already for stratified fluids, in two contexts complementary to the present study. First, the inertial effect of the stratification, neglected on the Boussinesq approximation, was considered in isolation by Eames & Hunt (Reference Eames and Hunt1997) and Palierne (Reference Palierne1999). Second, the creeping flow regime observed in sedimentation studies, reviewed by Ardekani, Doostmohammadi & Desai (Reference Ardekani, Doostmohammadi and Desai2017), Magnaudet & Mercier (Reference Magnaudet and Mercier2020) and More & Ardekani (Reference More and Ardekani2023), was considered by Candelier, Mehaddi & Vauquelin (Reference Candelier, Mehaddi and Vauquelin2014) at low Reynolds and Péclet numbers, showing that stratification induces a new memory force. No detailed comparison has been attempted with the present investigation. We note, however, that the response to the abrupt vertical motion of a sphere in figure 4 of Candelier et al. (Reference Candelier, Mehaddi and Vauquelin2014), made of damped oscillations at the buoyancy frequency towards an equilibrium value, is similar to the response in Voisin (Reference Voisin2024) after the abrupt release of a displaced spherical float.
An important limitation of the study is its neglect of the rotation of the body. Rotation is irrelevant – in the absence of viscosity – for the circular cylinder and the sphere for which this study was originally conceived (Voisin Reference Voisin2007, Reference Voisin2009), but it becomes essential for the elliptic cylinder and the spheroid; see the studies of settling discs by Lam, Vincent & Kanso (Reference Lam, Vincent and Kanso2019) and Mercier et al. (Reference Mercier, Wang, Péméja, Ern and Ardekani2020), and settling spheroids by More et al. (Reference More, Ardekani, Brandt and Ardekani2021) and Varanasi, Marath & Subramanian (Reference Varanasi, Marath and Subramanian2022). A choice was made here to focus on translation, in order to develop the mathematical and physical tools for added mass in a stratified fluid. Given the anisotropy of the fluid, an analytical approach of rotation may prove impossible except for the simplest geometries, since all symmetries are lost when the principal axes of the body deviate from the horizontal and the vertical. In two dimensions, the small angular oscillations of an elliptic cylinder of horizontal axis and inclined cross-section were considered by Hurley & Hood (Reference Hurley and Hood2001), theoretically, and its detailed dynamics by Hurlen (Reference Hurlen2006), theoretically, experimentally and numerically. In three dimensions, the small angular oscillations of horizontal discs were considered by Martin & Llewellyn Smith (Reference Martin and Llewellyn Smith2011, Reference Martin and Llewellyn Smith2012).
Other limitations are the uniformity of the stratification and the unboundedness of the fluid. The studies of two-layer and composite stratifications with or without top and bottom, mentioned in § 1, show the continued relevance of added mass for these configurations, closer to coastal areas. The similarity with surface gravity waves (Wehausen Reference Wehausen1971; Newman Reference Newman1978, Reference Newman2017, §§ 6.15–6.19) hints at the application of added mass to both radiation and scattering, and to the response of a body to incoming waves. The generation or scattering of an internal tide in an ocean of varying ![]() $N(z)$ and finite depth, in which the waves decompose into vertical modes, has been considered for two-dimensional topography by Pétrélis, Llewellyn Smith & Young (Reference Pétrélis, Llewellyn Smith and Young2006), Balmforth & Peacock (Reference Balmforth and Peacock2009), Echeverri & Peacock (Reference Echeverri and Peacock2010), Echeverri et al. (Reference Echeverri, Yokossi, Balmforth and Peacock2011) and Mathur, Carter & Peacock (Reference Mathur, Carter and Peacock2014). Boundary integrals were used, and the method turned into a software package (Mercier et al. Reference Mercier, Ghaemsaidi, Echeverri, Mathur and Peacock2012). Given the connection of the present investigation with boundary integrals, its adaptation to more realistic configurations does not seem far away. The flexibility of the added mass concept, tied to its deeply physical nature, is illustrated by the way in which added mass has been applied, in naval hydrodynamics, to floating bodies with elastic behaviour and resonances, and to fluids with an inclined bottom or an ice cover, or with a sea state, to name but a few adaptations.
$N(z)$ and finite depth, in which the waves decompose into vertical modes, has been considered for two-dimensional topography by Pétrélis, Llewellyn Smith & Young (Reference Pétrélis, Llewellyn Smith and Young2006), Balmforth & Peacock (Reference Balmforth and Peacock2009), Echeverri & Peacock (Reference Echeverri and Peacock2010), Echeverri et al. (Reference Echeverri, Yokossi, Balmforth and Peacock2011) and Mathur, Carter & Peacock (Reference Mathur, Carter and Peacock2014). Boundary integrals were used, and the method turned into a software package (Mercier et al. Reference Mercier, Ghaemsaidi, Echeverri, Mathur and Peacock2012). Given the connection of the present investigation with boundary integrals, its adaptation to more realistic configurations does not seem far away. The flexibility of the added mass concept, tied to its deeply physical nature, is illustrated by the way in which added mass has been applied, in naval hydrodynamics, to floating bodies with elastic behaviour and resonances, and to fluids with an inclined bottom or an ice cover, or with a sea state, to name but a few adaptations.
Acknowledgements
This research was initiated at DAMTP under the supervision of D. Crighton in 1998, then continued at LEGI. It benefited from numerous conversations with E. Ermanyuk and I. Sturova over the years, together with conversations with S. Llewellyn Smith and A. Davis during a stay at UCSD in 2008, correspondence with O. Bühler in 2009 and a conversation with J. Magnaudet in 2023. Input from A. Chikhi during a master internship in 2005 is acknowledged. The reviewers are thanked for their careful reading and suggestions, which led to substantial improvement of the paper.
Funding
This work was supported by Marie Curie grant ERBFMBI CT97 2653 from the European Commission (1998) and grant TOPOGI-3D from the French National Research Agency (2005–2008).
Declaration of interests
The author reports no conflict of interest.
Appendix A. Green's function
The impulsive Green's function ![]() $G(\boldsymbol {x},t)$ represents the response to a unit point impulse. It satisfies
$G(\boldsymbol {x},t)$ represents the response to a unit point impulse. It satisfies
with ![]() $\delta (\boldsymbol {x})\delta (t)$ the Dirac delta function, together with the causality condition
$\delta (\boldsymbol {x})\delta (t)$ the Dirac delta function, together with the causality condition ![]() $G|_{t<0} = 0$. It is continuous at
$G|_{t<0} = 0$. It is continuous at ![]() $t = 0$ and its derivative discontinuous, with
$t = 0$ and its derivative discontinuous, with
 \begin{equation} \left.G\right|_{t = 0_+} = 0, \quad \left.\frac{\partial G}{\partial t}\right|_{t = 0_+} ={-}\frac{1}{4{\rm \pi} r}, \end{equation}
\begin{equation} \left.G\right|_{t = 0_+} = 0, \quad \left.\frac{\partial G}{\partial t}\right|_{t = 0_+} ={-}\frac{1}{4{\rm \pi} r}, \end{equation}
where ![]() $r = |\boldsymbol {x}|$. Several expressions of the Green's function may be found in the literature, namely the convolution product
$r = |\boldsymbol {x}|$. Several expressions of the Green's function may be found in the literature, namely the convolution product
derived by Dickinson (Reference Dickinson1969) and Fox (Reference Fox1976), where ![]() $H(t)$ denotes the Heaviside step function and
$H(t)$ denotes the Heaviside step function and ![]() $\mathrm {J}_n(t)$ a Bessel function; the spectral integral
$\mathrm {J}_n(t)$ a Bessel function; the spectral integral
 \begin{equation} G(\boldsymbol{x},t) ={-}\frac{H(t)}{2{\rm \pi}^2r} \int_{N|z|/r}^N \frac{\sin(\omega t)} {(N^2-\omega^2)^{1/2}(\omega^2-N^2z^2/r^2)^{1/2}} \,\mathrm{d}\omega, \end{equation}
\begin{equation} G(\boldsymbol{x},t) ={-}\frac{H(t)}{2{\rm \pi}^2r} \int_{N|z|/r}^N \frac{\sin(\omega t)} {(N^2-\omega^2)^{1/2}(\omega^2-N^2z^2/r^2)^{1/2}} \,\mathrm{d}\omega, \end{equation}derived by Sekerzh-Zen'kovich (Reference Sekerzh-Zen'kovich1979, Reference Sekerzh-Zen'kovich1981b) and Teodorovich & Gorodtsov (Reference Teodorovich and Gorodtsov1980); and the series
 \begin{equation} G(\boldsymbol{x},t) ={-}\frac{H(t)}{2{\rm \pi} Nr} \sum_{n=0}^\infty \mathrm{J}_{2n+1}(Nt)P_n \Big(\frac{r_{h}^2-z^2}{r^2}\Big), \end{equation}
\begin{equation} G(\boldsymbol{x},t) ={-}\frac{H(t)}{2{\rm \pi} Nr} \sum_{n=0}^\infty \mathrm{J}_{2n+1}(Nt)P_n \Big(\frac{r_{h}^2-z^2}{r^2}\Big), \end{equation}
derived by Gorodtsov & Teodorovich (Reference Gorodtsov and Teodorovich1981) and Gordeichik & Ter-Krikorov (Reference Gordeichik and Ter-Krikorov1996), where ![]() $\boldsymbol {x}_{h} = (x,y,0)$ and
$\boldsymbol {x}_{h} = (x,y,0)$ and ![]() $r_{h} = |\boldsymbol {x}_{h}|$, and
$r_{h} = |\boldsymbol {x}_{h}|$, and ![]() $P_n(x)$ denotes a Legendre polynomial. The associated velocity
$P_n(x)$ denotes a Legendre polynomial. The associated velocity ![]() $\boldsymbol {u}_G = [(\partial ^2/\partial t^2)\boldsymbol {\nabla }+N^2\boldsymbol {\nabla }_{h}]G$ has the integral representation
$\boldsymbol {u}_G = [(\partial ^2/\partial t^2)\boldsymbol {\nabla }+N^2\boldsymbol {\nabla }_{h}]G$ has the integral representation
 \begin{align} \boldsymbol{u}_G(\boldsymbol{x},t) & = \frac{\boldsymbol{x}}{2{\rm \pi}^2r^3} \frac{\partial}{\partial t} \left\{ H(t) \left[ \frac{\rm \pi}{2}\cos\left(Nt\frac{|z|}{r}\right) \right. \right.\nonumber\\ & \quad \left. \left. + \int_{N|z|/r}^N \frac{\omega(N^2-\omega^2)^{1/2}} {(\omega^2-N^2z^2/r^2)^{3/2}} \left[\cos\left(Nt\frac{|z|}{r}\right)-\cos(\omega t)\right] \,\mathrm{d}\omega \right] \right\}, \end{align}
\begin{align} \boldsymbol{u}_G(\boldsymbol{x},t) & = \frac{\boldsymbol{x}}{2{\rm \pi}^2r^3} \frac{\partial}{\partial t} \left\{ H(t) \left[ \frac{\rm \pi}{2}\cos\left(Nt\frac{|z|}{r}\right) \right. \right.\nonumber\\ & \quad \left. \left. + \int_{N|z|/r}^N \frac{\omega(N^2-\omega^2)^{1/2}} {(\omega^2-N^2z^2/r^2)^{3/2}} \left[\cos\left(Nt\frac{|z|}{r}\right)-\cos(\omega t)\right] \,\mathrm{d}\omega \right] \right\}, \end{align}derived by Zavol'skii & Zaitsev (Reference Zavol'skii and Zaitsev1984).
Another singular solution has been used by Miropol'skii (Reference Miropol'skii1978) and Gabov & Shevtsov (Reference Gabov and Shevtsov1983),
based on an analogy with the known Green's function of inertial waves (Sobolev Reference Sobolev1954; Maslennikova Reference Maslennikova1968). It was shown by Teodorovich & Gorodtsov (Reference Teodorovich and Gorodtsov1980) to satisfy
instead of (A1). The two solutions are related to each other by
and their spectra by
so that
and conversely,
as remarked by Gabov & Shevtsov (Reference Gabov and Shevtsov1986).
Appendix B. Kirchhoff–Helmholtz integral
The initial-boundary value problem for inertial waves was solved by Sobolev (Reference Sobolev1954) in terms of a Kirchhoff–Helmholtz integral, and the integral applied by him to initial values and by Kapitonov (Reference Kapitonov1980) to boundary values. For internal waves, a Kirchhoff–Helmholtz integral was derived by Miropol'skii (Reference Miropol'skii1978) and Gabov & Shevtsov (Reference Gabov and Shevtsov1983), using ![]() $F(\boldsymbol {x},t)$ as a Green's function, with Pletner (Reference Pletner1991) adding non-Boussinesq effects and Sundukova (Reference Sundukova1991) rotation. Sekerzh-Zen'kovich (Reference Sekerzh-Zen'kovich1981a, Reference Sekerzh-Zen'kovich1982) solved the initial-value problem in terms of the actual Green's function
$F(\boldsymbol {x},t)$ as a Green's function, with Pletner (Reference Pletner1991) adding non-Boussinesq effects and Sundukova (Reference Sundukova1991) rotation. Sekerzh-Zen'kovich (Reference Sekerzh-Zen'kovich1981a, Reference Sekerzh-Zen'kovich1982) solved the initial-value problem in terms of the actual Green's function ![]() $G(\boldsymbol {x},t)$, and Simakov (Reference Simakov1993) introduced the use of an unspecified Green's function tailored to the Dirichlet boundary condition.
$G(\boldsymbol {x},t)$, and Simakov (Reference Simakov1993) introduced the use of an unspecified Green's function tailored to the Dirichlet boundary condition.
We derive the Kirchhoff–Helmholtz integral for unsteady internal waves by following the same lines as for the classical wave equation (Morse & Feshbach Reference Morse and Feshbach1953, pp. 834–837). For arbitrary functions ![]() $f$ and
$f$ and ![]() $g$, we write
$g$, we write
 \begin{align} &f \left(\frac{\partial^2}{\partial t^2}\nabla^2+N^2\nabla_{h}^2\right)g- g \left(\frac{\partial^2}{\partial t^2}\nabla^2+N^2\nabla_{h}^2\right)f\nonumber\\ &\quad = \frac{\partial}{\partial t} \left( \nabla^2f\frac{\partial g}{\partial t} - g\frac{\partial}{\partial t}\nabla^2f \right) - \frac{\partial}{\partial t}\boldsymbol{\nabla}\boldsymbol{\cdot} \left(\boldsymbol{\nabla} f\frac{\partial g}{\partial t} - g\frac{\partial}{\partial t}\boldsymbol{\nabla} f \right)\nonumber\\ &\qquad + \boldsymbol{\nabla}\boldsymbol{\cdot} \left[ f \left(\frac{\partial^2}{\partial t^2}\boldsymbol{\nabla}+N^2\boldsymbol{\nabla}_{h} \right) g - g \left( \frac{\partial^2}{\partial t^2}\boldsymbol{\nabla}+N^2\boldsymbol{\nabla}_{h} \right)f \right], \end{align}
\begin{align} &f \left(\frac{\partial^2}{\partial t^2}\nabla^2+N^2\nabla_{h}^2\right)g- g \left(\frac{\partial^2}{\partial t^2}\nabla^2+N^2\nabla_{h}^2\right)f\nonumber\\ &\quad = \frac{\partial}{\partial t} \left( \nabla^2f\frac{\partial g}{\partial t} - g\frac{\partial}{\partial t}\nabla^2f \right) - \frac{\partial}{\partial t}\boldsymbol{\nabla}\boldsymbol{\cdot} \left(\boldsymbol{\nabla} f\frac{\partial g}{\partial t} - g\frac{\partial}{\partial t}\boldsymbol{\nabla} f \right)\nonumber\\ &\qquad + \boldsymbol{\nabla}\boldsymbol{\cdot} \left[ f \left(\frac{\partial^2}{\partial t^2}\boldsymbol{\nabla}+N^2\boldsymbol{\nabla}_{h} \right) g - g \left( \frac{\partial^2}{\partial t^2}\boldsymbol{\nabla}+N^2\boldsymbol{\nabla}_{h} \right)f \right], \end{align}
which, integrated in time from ![]() $t_1$ to
$t_1$ to ![]() $t_2$ and in space over a volume
$t_2$ and in space over a volume ![]() $V$ delimited by the surface
$V$ delimited by the surface ![]() $S$ of outward normal
$S$ of outward normal ![]() $\boldsymbol {n}$, gives
$\boldsymbol {n}$, gives
 \begin{align} & \int_{t_1}^{t_2}\,\mathrm{d}t\int_V\,\mathrm{d}^3x \left[ f\left(\frac{\partial^2}{\partial t^2}\nabla^2+N^2\nabla_{h}^2\right)g- g\left(\frac{\partial^2}{\partial t^2}\nabla^2+N^2\nabla_{h}^2\right)f \right] \nonumber\\ & \quad = \int_V\,\mathrm{d}^3x\, \left[ \nabla^2f\frac{\partial g}{\partial t} - g\frac{\partial}{\partial t}\nabla^2f \right]_{t = t_1}^{t = t_2} - \int_S\,\mathrm{d}^2S\left[ \frac{\partial f}{\partial n}\frac{\partial g}{\partial t} - g\frac{\partial}{\partial t}\frac{\partial f}{\partial n} \right]_{t = t_1}^{t = t_2} \nonumber\\ & \qquad + \int_{t_1}^{t_2}\,\mathrm{d}t\int_S\,\mathrm{d}^2S \left[ f \left( \frac{\partial^2}{\partial t^2}\frac{\partial}{\partial n}+N^2\frac{\partial}{\partial n_{h}} \right) g - g \left( \frac{\partial^2}{\partial t^2}\frac{\partial}{\partial n}+N^2\frac{\partial}{\partial n_{h}} \right) f \right]. \end{align}
\begin{align} & \int_{t_1}^{t_2}\,\mathrm{d}t\int_V\,\mathrm{d}^3x \left[ f\left(\frac{\partial^2}{\partial t^2}\nabla^2+N^2\nabla_{h}^2\right)g- g\left(\frac{\partial^2}{\partial t^2}\nabla^2+N^2\nabla_{h}^2\right)f \right] \nonumber\\ & \quad = \int_V\,\mathrm{d}^3x\, \left[ \nabla^2f\frac{\partial g}{\partial t} - g\frac{\partial}{\partial t}\nabla^2f \right]_{t = t_1}^{t = t_2} - \int_S\,\mathrm{d}^2S\left[ \frac{\partial f}{\partial n}\frac{\partial g}{\partial t} - g\frac{\partial}{\partial t}\frac{\partial f}{\partial n} \right]_{t = t_1}^{t = t_2} \nonumber\\ & \qquad + \int_{t_1}^{t_2}\,\mathrm{d}t\int_S\,\mathrm{d}^2S \left[ f \left( \frac{\partial^2}{\partial t^2}\frac{\partial}{\partial n}+N^2\frac{\partial}{\partial n_{h}} \right) g - g \left( \frac{\partial^2}{\partial t^2}\frac{\partial}{\partial n}+N^2\frac{\partial}{\partial n_{h}} \right) f \right]. \end{align} This Green's theorem is applied to wave generation by an initial disturbance at time ![]() $t = 0$ followed by boundary forcing at a closed surface
$t = 0$ followed by boundary forcing at a closed surface ![]() $S$ at times
$S$ at times ![]() $t > 0$. We choose a fixed observation time
$t > 0$. We choose a fixed observation time ![]() $t > 0$, and a fixed observation point
$t > 0$, and a fixed observation point ![]() $\boldsymbol {x}$ situated either inside
$\boldsymbol {x}$ situated either inside ![]() $S$ in the domain
$S$ in the domain ![]() $V_-$ or outside
$V_-$ or outside ![]() $S$ in the domain
$S$ in the domain ![]() $V_+$. We integrate over
$V_+$. We integrate over ![]() $t'$ in the interval
$t'$ in the interval ![]() $[0,t]$ and over
$[0,t]$ and over ![]() $\boldsymbol {x}'$ in the domain bounded internally by
$\boldsymbol {x}'$ in the domain bounded internally by ![]() $S$ and externally by a sphere
$S$ and externally by a sphere ![]() $S_R$ of centre at
$S_R$ of centre at ![]() $\boldsymbol {x}$ and large radius
$\boldsymbol {x}$ and large radius ![]() $R$, as shown in figure 12. We take, for
$R$, as shown in figure 12. We take, for ![]() $f$, the internal potential
$f$, the internal potential ![]() $\psi (\boldsymbol {x}',t')$ and, for
$\psi (\boldsymbol {x}',t')$ and, for ![]() $g$, the propagator
$g$, the propagator ![]() $G(\boldsymbol {x}-\boldsymbol {x}',t-t')$, with
$G(\boldsymbol {x}-\boldsymbol {x}',t-t')$, with ![]() $G$ the Green's function. The contribution of
$G$ the Green's function. The contribution of ![]() $S_R$ is assumed to vanish in the limit
$S_R$ is assumed to vanish in the limit ![]() $R \to \infty$, an assumption we will come back to later.
$R \to \infty$, an assumption we will come back to later.

Figure 12. Geometry for the derivation of the Kirchhoff–Helmholtz integral.
We obtain
 \begin{align} H_+(\boldsymbol{x})\psi(\boldsymbol{x},t) & = \int_{V_+}\,\mathrm{d}^3x' \left[ \nabla'^2\psi_0(\boldsymbol{x}')\frac{\partial G}{\partial t}(\boldsymbol{x}-\boldsymbol{x}',t) + \nabla'^2\psi_1(\boldsymbol{x}')G(\boldsymbol{x}-\boldsymbol{x}',t) \right] \nonumber\\ & \quad + \int_S\,\mathrm{d}^2S' \left[ \frac{\partial\psi_0}{\partial n'}(\boldsymbol{x}')\frac{\partial G}{\partial t}(\boldsymbol{x}-\boldsymbol{x}',t) + \frac{\partial\psi_1}{\partial n'}(\boldsymbol{x}')G(\boldsymbol{x}-\boldsymbol{x}',t) \right] \nonumber\\ & \quad + \int_0^{t+0}\,\mathrm{d}t'\int_S\,\mathrm{d}^2S' \left[ G(\boldsymbol{x}-\boldsymbol{x}',t-t') \left( \frac{\partial^2}{\partial t'^2}\frac{\partial}{\partial n'} +N^2\frac{\partial}{\partial n'_{h}} \right) \psi(\boldsymbol{x}',t') \right. \nonumber\\ & \quad\left. - \psi(\boldsymbol{x}',t') \left( \frac{\partial^2}{\partial t'^2}\frac{\partial}{\partial n'} +N^2\frac{\partial}{\partial n'_{h}} \right) G(\boldsymbol{x}-\boldsymbol{x}',t-t') \right], \end{align}
\begin{align} H_+(\boldsymbol{x})\psi(\boldsymbol{x},t) & = \int_{V_+}\,\mathrm{d}^3x' \left[ \nabla'^2\psi_0(\boldsymbol{x}')\frac{\partial G}{\partial t}(\boldsymbol{x}-\boldsymbol{x}',t) + \nabla'^2\psi_1(\boldsymbol{x}')G(\boldsymbol{x}-\boldsymbol{x}',t) \right] \nonumber\\ & \quad + \int_S\,\mathrm{d}^2S' \left[ \frac{\partial\psi_0}{\partial n'}(\boldsymbol{x}')\frac{\partial G}{\partial t}(\boldsymbol{x}-\boldsymbol{x}',t) + \frac{\partial\psi_1}{\partial n'}(\boldsymbol{x}')G(\boldsymbol{x}-\boldsymbol{x}',t) \right] \nonumber\\ & \quad + \int_0^{t+0}\,\mathrm{d}t'\int_S\,\mathrm{d}^2S' \left[ G(\boldsymbol{x}-\boldsymbol{x}',t-t') \left( \frac{\partial^2}{\partial t'^2}\frac{\partial}{\partial n'} +N^2\frac{\partial}{\partial n'_{h}} \right) \psi(\boldsymbol{x}',t') \right. \nonumber\\ & \quad\left. - \psi(\boldsymbol{x}',t') \left( \frac{\partial^2}{\partial t'^2}\frac{\partial}{\partial n'} +N^2\frac{\partial}{\partial n'_{h}} \right) G(\boldsymbol{x}-\boldsymbol{x}',t-t') \right], \end{align}
where ![]() $H_+(\boldsymbol {x}) = 1$ for
$H_+(\boldsymbol {x}) = 1$ for ![]() $\boldsymbol {x} \in V_+$ and
$\boldsymbol {x} \in V_+$ and ![]() $0$ for
$0$ for ![]() $\boldsymbol {x} \in V_-$ is the Heaviside step function of support
$\boldsymbol {x} \in V_-$ is the Heaviside step function of support ![]() $V_+$. The first integral on the right-hand side includes the initial disturbance
$V_+$. The first integral on the right-hand side includes the initial disturbance
and is Sekerzh-Zen'kovich's (Reference Sekerzh-Zen'kovich1981a, Reference Sekerzh-Zen'kovich1982) solution of the initial-value problem in the whole space. The second integral adds another initial contribution when a boundary is present. The third integral represents the effect of the subsequent boundary forcing. It combines a single-layer potential of the general form
and a double-layer potential of the form
with ![]() $\sigma$ and
$\sigma$ and ![]() $\mu$ the respective surface densities. The notation
$\mu$ the respective surface densities. The notation ![]() $t+0$ means that the temporal integration ends immediately after
$t+0$ means that the temporal integration ends immediately after ![]() $t$. If it were to end at
$t$. If it were to end at ![]() $t-0$, immediately before
$t-0$, immediately before ![]() $t$, then an additional term would arise,
$t$, then an additional term would arise,
associated with the delta-function singularity of ![]() $\partial ^2G/\partial t'^2(\boldsymbol {x}-\boldsymbol {x}',t-t')$ at
$\partial ^2G/\partial t'^2(\boldsymbol {x}-\boldsymbol {x}',t-t')$ at ![]() $t' = t$. This term may be seen in Kapitonov (Reference Kapitonov1980), Gabov & Shevtsov (Reference Gabov and Shevtsov1983) and Simakov (Reference Simakov1993).
$t' = t$. This term may be seen in Kapitonov (Reference Kapitonov1980), Gabov & Shevtsov (Reference Gabov and Shevtsov1983) and Simakov (Reference Simakov1993).
The omitted contribution of ![]() $S_R$ includes two parts. The first part,
$S_R$ includes two parts. The first part,
is associated with the initial disturbance. It vanishes as ![]() $R \to \infty$ provided that
$R \to \infty$ provided that
which are the conditions on which Sekerzh-Zen'kovich's (Reference Sekerzh-Zen'kovich1981a, Reference Sekerzh-Zen'kovich1982) solution has been obtained. The second part,
potentially includes waves both radiating away from the forcing and coming in from infinity. A radiation condition is needed to eliminate the latter. For steady monochromatic waves, considered in Voisin (Reference Voisin2021), the radiation condition assumes different forms inside and outside the wave beams; this is linked to the singularity of the monochromatic Green's function along the wave rays. Here for unsteady waves, the impulsive Green's function possesses no such singularity. As ![]() $R \to \infty$, we have
$R \to \infty$, we have
and the radiation condition consists in requiring that the waves decay at the same rate,
With the area element ![]() $\mathrm {d}^2S'$ varying as
$\mathrm {d}^2S'$ varying as ![]() $R^2$, (B10) varies as
$R^2$, (B10) varies as ![]() $1/R$ and vanishes as
$1/R$ and vanishes as ![]() $R \to \infty$. Sobolev (Reference Sobolev1954) noted that his (154), essentially (B2) for inertial waves, could be applied to an unbounded domain
$R \to \infty$. Sobolev (Reference Sobolev1954) noted that his (154), essentially (B2) for inertial waves, could be applied to an unbounded domain ![]() $V$ provided that
$V$ provided that ![]() $f$ and
$f$ and ![]() $g$ decayed at infinity as
$g$ decayed at infinity as ![]() $1/R$, their first-order spatial derivatives as
$1/R$, their first-order spatial derivatives as ![]() $1/R^2$ and the second-order derivatives as
$1/R^2$ and the second-order derivatives as ![]() $1/R^3$.
$1/R^3$.
Boundary forcing is singled out by considering motion started from rest at ![]() $t = -\infty$. We have
$t = -\infty$. We have
 \begin{align} H_+(\boldsymbol{x})\psi(\boldsymbol{x},t) & = \int_{-\infty}^{t+0}\,\mathrm{d}t'\int_S\,\mathrm{d}^2S'\, \left[ G(\boldsymbol{x}-\boldsymbol{x}',t-t') \left( \frac{\partial^2}{\partial t'^2}\frac{\partial}{\partial n'} +N^2\frac{\partial}{\partial n'_{h}} \right) \psi(\boldsymbol{x}',t') \right. \nonumber\\ & \quad \left. - \psi(\boldsymbol{x}',t') \left( \frac{\partial^2}{\partial t'^2}\frac{\partial}{\partial n'} +N^2\frac{\partial}{\partial n'_{h}} \right) G(\boldsymbol{x}-\boldsymbol{x}',t-t') \right], \end{align}
\begin{align} H_+(\boldsymbol{x})\psi(\boldsymbol{x},t) & = \int_{-\infty}^{t+0}\,\mathrm{d}t'\int_S\,\mathrm{d}^2S'\, \left[ G(\boldsymbol{x}-\boldsymbol{x}',t-t') \left( \frac{\partial^2}{\partial t'^2}\frac{\partial}{\partial n'} +N^2\frac{\partial}{\partial n'_{h}} \right) \psi(\boldsymbol{x}',t') \right. \nonumber\\ & \quad \left. - \psi(\boldsymbol{x}',t') \left( \frac{\partial^2}{\partial t'^2}\frac{\partial}{\partial n'} +N^2\frac{\partial}{\partial n'_{h}} \right) G(\boldsymbol{x}-\boldsymbol{x}',t-t') \right], \end{align}which becomes, after integrating the double-layer term twice by parts over time and using the reciprocity of the Green's function,
 \begin{align} H_+(\boldsymbol{x})\psi(\boldsymbol{x},t) & = \int_{-\infty}^t\,\mathrm{d}t' \int_S\,\mathrm{d}^2S'\, \left[ G(\boldsymbol{x}-\boldsymbol{x}',t-t') \left( \frac{\partial^2}{\partial t'^2}\frac{\partial}{\partial n'} +N^2\frac{\partial}{\partial n'_{h}} \right) \psi(\boldsymbol{x}',t') \right. \nonumber\\ & \quad \left. + \left( \boldsymbol{n}'\frac{\partial^2}{\partial t'^2} +\boldsymbol{n}'_\mathrm{h}N^2 \right) \psi(\boldsymbol{x}',t') \boldsymbol{\cdot} \boldsymbol{\nabla} G(\boldsymbol{x}-\boldsymbol{x}',t-t') \right]. \end{align}
\begin{align} H_+(\boldsymbol{x})\psi(\boldsymbol{x},t) & = \int_{-\infty}^t\,\mathrm{d}t' \int_S\,\mathrm{d}^2S'\, \left[ G(\boldsymbol{x}-\boldsymbol{x}',t-t') \left( \frac{\partial^2}{\partial t'^2}\frac{\partial}{\partial n'} +N^2\frac{\partial}{\partial n'_{h}} \right) \psi(\boldsymbol{x}',t') \right. \nonumber\\ & \quad \left. + \left( \boldsymbol{n}'\frac{\partial^2}{\partial t'^2} +\boldsymbol{n}'_\mathrm{h}N^2 \right) \psi(\boldsymbol{x}',t') \boldsymbol{\cdot} \boldsymbol{\nabla} G(\boldsymbol{x}-\boldsymbol{x}',t-t') \right]. \end{align}
The singularity at ![]() $t' = t$ is now gone. At large distances
$t' = t$ is now gone. At large distances ![]() $|\boldsymbol {x}| \gg |\boldsymbol {x}'|$ from the forcing, a multipole expansion follows from expanding the Green's function in the form
$|\boldsymbol {x}| \gg |\boldsymbol {x}'|$ from the forcing, a multipole expansion follows from expanding the Green's function in the form
and writing
with ![]() $u_n = \boldsymbol {n}\boldsymbol {\cdot }\boldsymbol {u}$ the normal velocity on
$u_n = \boldsymbol {n}\boldsymbol {\cdot }\boldsymbol {u}$ the normal velocity on ![]() $S$. We obtain
$S$. We obtain
where
is the monopole strength of the forcing and
its dipole strength.
Appendix C. Some inverse Fourier transforms
The following integrals, related to inverse Fourier transforms, are used in the present Part 1 and the companion Part 2.
First come integrals around a cut along the negative imaginary axis, shown in figure 13(a). The contour starts at infinity on the left side of the cut, encircles the branch point at the origin in the clockwise sense then goes back to infinity on the right-hand side. The integrals are
 \begin{gather} \frac{1}{2{\rm \pi}}\int_{-\mathrm{i}\infty}^{(0_-)} \frac{\exp(-\mathrm{i}\omega t)}{\omega^{1/2}\pm\omega_0^{1/2}} \,\mathrm{d}\omega = \frac{\mathrm{e}^{-\mathrm{i}{\rm \pi}/4}}{({\rm \pi} t)^{1/2}} + \mathrm{i}\omega_0^{1/2} \exp(-\mathrm{i}\omega_0t) \operatorname{erfc}[(\omega_0t)^{1/2}\mathrm{e}^{-\mathrm{i}{\rm \pi}/4}], \end{gather}
\begin{gather} \frac{1}{2{\rm \pi}}\int_{-\mathrm{i}\infty}^{(0_-)} \frac{\exp(-\mathrm{i}\omega t)}{\omega^{1/2}\pm\omega_0^{1/2}} \,\mathrm{d}\omega = \frac{\mathrm{e}^{-\mathrm{i}{\rm \pi}/4}}{({\rm \pi} t)^{1/2}} + \mathrm{i}\omega_0^{1/2} \exp(-\mathrm{i}\omega_0t) \operatorname{erfc}[(\omega_0t)^{1/2}\mathrm{e}^{-\mathrm{i}{\rm \pi}/4}], \end{gather}
where ![]() $n$ is a non-negative integer,
$n$ is a non-negative integer, ![]() $\mu \ne -n$ a real number,
$\mu \ne -n$ a real number, ![]() $\varGamma (\mu )$ the gamma function,
$\varGamma (\mu )$ the gamma function, ![]() $\omega _0$ a complex number such that
$\omega _0$ a complex number such that ![]() $\mathrm {Im}[(\mathrm {i}\omega _0)^{1/2}] > 0$ and
$\mathrm {Im}[(\mathrm {i}\omega _0)^{1/2}] > 0$ and ![]() $\operatorname {erfc} t$ the complementary error function.
$\operatorname {erfc} t$ the complementary error function.

Figure 13. Integration contours for the inverse transforms in Appendix C.
Then come integrals along portions of that contour, namely
 \begin{equation} \frac{1}{2{\rm \pi}}\int_{-\mathrm{i}}^{(0_-)} \exp(-\mathrm{i}\omega t)\omega^n \ln\omega \,\mathrm{d}\omega ={-}\frac{n!}{\mathrm{i}^nt^{n+1}} \Big[ 1-\exp({-}t)\sum_{k = 0}^n\frac{t^k}{k!} \Big], \end{equation}
\begin{equation} \frac{1}{2{\rm \pi}}\int_{-\mathrm{i}}^{(0_-)} \exp(-\mathrm{i}\omega t)\omega^n \ln\omega \,\mathrm{d}\omega ={-}\frac{n!}{\mathrm{i}^nt^{n+1}} \Big[ 1-\exp({-}t)\sum_{k = 0}^n\frac{t^k}{k!} \Big], \end{equation}taken along the path shown in figure 13(b), and
taken along the path shown in figure 13(c), with ![]() $\gamma ^\ast (\mu,t) = t^{-\mu }\gamma (\mu,t)/\varGamma (\mu )$ a normalized form of the incomplete gamma function
$\gamma ^\ast (\mu,t) = t^{-\mu }\gamma (\mu,t)/\varGamma (\mu )$ a normalized form of the incomplete gamma function ![]() $\gamma (\mu,t)$.
$\gamma (\mu,t)$.