Article contents
Acoustic streaming and the induced forces between two spheres
Published online by Cambridge University Press: 25 November 2016
Abstract
The ability of acoustic microstreaming to cause a pair of particles to attract or repel is investigated. Expanding the flow around two spheres in terms of a small-amplitude parameter measuring the amplitude of the forcing, the leading order is an oscillating flow field with zero mean representing the effect of the applied acoustic field, while the second-order correction contains a steady streaming component. A modal decomposition in the azimuthal direction reduces the problem to a few linear problems in a two-dimensional domain corresponding to the meridional (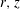 $r,z$) plane. The analysis computes both the intricate flow fields and the mean forces felt by both spheres. If the spheres are aligned obliquely with respect to the oscillating flow, they experience a lateral force which realigns them into a transverse configuration. In this transverse configuration, they experience an axial force which can be either attractive or repulsive. At high frequencies the force is always attractive. At low frequencies, it is repulsive. At intermediate frequencies, the force is attractive at large distances and repulsive at small distances, leading to the existence of a stable equilibrium configuration.
$r,z$) plane. The analysis computes both the intricate flow fields and the mean forces felt by both spheres. If the spheres are aligned obliquely with respect to the oscillating flow, they experience a lateral force which realigns them into a transverse configuration. In this transverse configuration, they experience an axial force which can be either attractive or repulsive. At high frequencies the force is always attractive. At low frequencies, it is repulsive. At intermediate frequencies, the force is attractive at large distances and repulsive at small distances, leading to the existence of a stable equilibrium configuration.
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 8
- Cited by



