Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-24T17:57:59.005Z Has data issue: false hasContentIssue false
  • English
  • Français

Acoustic oscillations driven by boundary mass exchange

Published online by Cambridge University Press:  05 March 2019

Avshalom Offner ,
Rui Yang ,
Daniel Felman ,
Nimrod Elkayam ,
Yehuda Agnon  and
Guy Z. Ramon Open the ORCID record for Guy Z. Ramon [Opens in a new window]
Avshalom Offner
Affiliation:
The Nancy and Stephen Grand Technion Energy Programme, Technion – Israel Institute of Technology, Haifa 32000, Israel Department of Civil and Environmental Engineering, Technion – Israel Institute of Technology, Haifa 32000, Israel
Rui Yang
Affiliation:
Department of Civil and Environmental Engineering, Technion – Israel Institute of Technology, Haifa 32000, Israel
Daniel Felman
Affiliation:
Department of Civil and Environmental Engineering, Technion – Israel Institute of Technology, Haifa 32000, Israel The Applied Mathematics Interdisciplinary Graduate Programme, Technion – Israel Institute of Technology, Haifa 32000, Israel
Nimrod Elkayam
Affiliation:
The Nancy and Stephen Grand Technion Energy Programme, Technion – Israel Institute of Technology, Haifa 32000, Israel Department of Civil and Environmental Engineering, Technion – Israel Institute of Technology, Haifa 32000, Israel
Yehuda Agnon
Affiliation:
The Nancy and Stephen Grand Technion Energy Programme, Technion – Israel Institute of Technology, Haifa 32000, Israel Department of Civil and Environmental Engineering, Technion – Israel Institute of Technology, Haifa 32000, Israel The Applied Mathematics Interdisciplinary Graduate Programme, Technion – Israel Institute of Technology, Haifa 32000, Israel Millstone/St. Louis Chair in Civil/Environmental Engineering, Technion – Israel Institute of Technology, Haifa 32000, Israel
Guy Z. Ramon*
Affiliation:
The Nancy and Stephen Grand Technion Energy Programme, Technion – Israel Institute of Technology, Haifa 32000, Israel Department of Civil and Environmental Engineering, Technion – Israel Institute of Technology, Haifa 32000, Israel The Applied Mathematics Interdisciplinary Graduate Programme, Technion – Israel Institute of Technology, Haifa 32000, Israel
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Thermoacoustic instability – self-sustained pressure oscillations triggered by temperature gradients – has become an increasingly studied topic in the context of energy conversion. Generally, the process relies on conductive heat transfer between a solid and the fluid in which the generated pressure oscillations are sustained. In the present study, the thermoacoustic theory is extended to include mass transfer; specifically, the working fluid is modified so as to incorporate a ‘reactive’ gas, able to exchange phase with a solid/liquid boundary through a sorption process (or through evaporation/condensation), such that most heat is transferred in the form of latent heat rather than through conduction. A set of differential equations is derived, accounting for phase-exchange heat and mass transfer, and de-coupled via a small-amplitude asymptotic expansion. These equations are solved and subsequently manipulated into the form of a wave equation, representing the small perturbation on the pressure field, and used to derive expressions for the time-averaged, second-order heat and mass fluxes. A stability analysis is performed on the wave equation, from which the marginal stability curve is calculated in terms of the temperature difference, 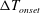$\unicode[STIX]{x0394}T_{onset}$, required for initiation of self-sustained oscillations. Calculated stability curves are compared with published experimental results, showing good agreement. Effects of gas mixture composition are studied, indicating that a lower heat capacity of the inert component, combined with a low boiling temperature and high latent heat of the reactive component substantially lower 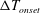$\unicode[STIX]{x0394}T_{onset}$. Furthermore, an increase in the average mole fraction of the reactive gas, 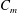$C_{m}$ strongly affects onset conditions, leading to 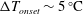$\unicode[STIX]{x0394}T_{onset}\sim 5\,^{\circ }\text{C}$ at the highest value of 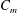$C_{m}$ achievable under atmospheric pressure. An analysis of the system limit cycle is performed for a wide range of parameters, indicating a systematic decrease in the temperature difference capable of sustaining the limit cycle, as well as a significant distortion of the acoustic wave form as the phase-exchange mechanism becomes dominant. These findings, combined, reveal the underlying mechanisms by which a phase-exchange engine may produce more acoustic power than its counterpart ‘classical’ thermoacoustic system, while its temperature difference is substantially lower.

JFM classification

Phase change: Phase change Instability: Instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 866 , 10 May 2019 , pp. 316 - 349
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arnott, W. P., Bass, H. E. & Raspet, R. 1992 Specific acoustic impedance measurements of an air-filled thermoacoustic prime mover. J. Acoust. Soc. Am. 92 (6), 3432–3434.10.1121/1.404167Google Scholar
Arnott, W. P., Belcher, J. R., Raspet, R. & Bass, H. E. 1994 Stability analysis of a helium-filled thermoacoustic engine. J. Acoust. Soc. Am. 96 (1), 370–375.10.1121/1.410486Google Scholar
Bird, R. B., Stewart, W. E. & Lightfoot, E. N. 2007 Transport Phenomena, 2nd edn. Wiley.Google Scholar
Ceperley, P. H. 1979 A pistonless Stirling engine – the traveling wave heat engine. J. Acoust. Soc. Am. 66 (5), 1508–1513.10.1121/1.383505Google Scholar
Dowling, A. P. & Morgans, A. S. 2005 Feedback control of combustion oscillations. Annu. Rev. Fluid Mech. 37 (1), 151–182.10.1146/annurev.fluid.36.050802.122038Google Scholar
Fleifil, M., Annaswamy, A. M., Ghoneim, Z. A. & Ghoniem, A. F. 1996 Response of a laminar premixed flame to flow oscillations: a kinematic model and thermoacoustic instability results. Combust. Flame 106 (4), 487–510.10.1016/0010-2180(96)00049-1Google Scholar
Hiller, R. A. & Swift, G. W. 2000 Condensation in a steady-flow thermoacoustic refrigerator. J. Acoust. Soc. Am. 108 (4), 1521–1527.10.1121/1.1289664Google Scholar
Keller, J. J. 1995 Thermoacoustic oscillations in combustion chambers of gas turbines. AIAA J. 33 (12), 2280–2287.10.2514/3.12980Google Scholar
Landau, L. D. & Lifshitz, E. M. 1959 Fluid Mechanics. Pergamon.Google Scholar
Majer, V. & Svoboda, V. 1985 Enthalpies of Vaporization of Organic Compounds: A Critical Review and Data Compilation. Blackwell Scientific.Google Scholar
Meir, A., Offner, A. & Ramon, G. Z. 2018 Low-temperature energy conversion using a phase-change acoustic heat engine. Applied Energy 231, 372–379.10.1016/j.apenergy.2018.09.124Google Scholar
Noda, D. & Ueda, Y. 2013 A thermoacoustic oscillator powered by vaporized water and ethanol. Am. J. Phys. 81 (2), 124–126.10.1119/1.4766940Google Scholar
Poling, B. E., Prausnitz, J. M. & O’Connell, J. P. 2001 The Properties of Gases and Liquids. McGraw-Hill.Google Scholar
Raspet, R., Slaton, W. V., Hickey, C. J. & Hiller, R. A. 2002 Theory of inert gas-condensing vapor thermoacoustics: propgation equations. J. Acoust. Soc. Am. 112 (4), 1414–1422.10.1121/1.1508113Google Scholar
Rijke, P. L. 1859 Notiz über eine neue Art, die in einer an beiden Enden offenen Röhre enthaltene Luft in Schwingungen zu versetzen. Ann. Phys. 183 (6), 339–343.10.1002/andp.18591830616Google Scholar
Rott, N. 1969 Damped and thermally driven acoustic oscillations in wide and narrow tubes. Z. Angew. Math. Phys. 20 (2), 230–243.10.1007/BF01595562Google Scholar
Slaton, W. V., Raspet, R., Hickey, C. J. & Hiller, R. A. 2002 Theory of inert gas-condensing vapor thermoacoustics: transport equations. J. Acoust. Soc. Am. 112 (4), 1423–1430.10.1121/1.1508114Google Scholar
Sondhauss, C. 1850 Ueber die Schallschwingungen der Luft in erhitzten Glasröhren und in gedeckten Pfeifen von ungleicher Weite. Ann. Phys. 155 (1), 1–34.10.1002/andp.18501550102Google Scholar
Swift, G. W. 1988 Thermoacoustic engines. J. Acoust. Soc. Am. 84 (4), 1145–1180.10.1121/1.396617Google Scholar
Swift, G. W. 1992 Analysis and performance of a large thermoacoustic engine. J. Acoust. Soc. Am. 92 (3), 1551–1563.10.1121/1.403896Google Scholar
Swift, G. W. 2002 Thermoacoustics: A Unifying Perspective for Some Engines and Refrigerators. Acoustic Society of America.Google Scholar
Tsuda, K. & Ueda, Y. 2015 Abrupt reduction of the critical temperature difference of a thermoacoustic engine by adding water. AIP Adv. 5 (9), 097173.10.1063/1.4932036Google Scholar
Tsuda, K. & Ueda, Y. 2017 Critical temperature of traveling- and standing-wave thermoacoustic engines using a wet regenerator. Appl. Energy 196, 62–67.10.1016/j.apenergy.2017.04.004Google Scholar
Ward, W. C. & Swift, G. W. 1994 Design environment for low amplitude thermoacoustic engines. J. Acoust. Soc. Am. 95 (6), 3671–3672.10.1121/1.409938Google Scholar
Weltsch, O., Offner, A., Liberzon, D. & Ramon, G. Z. 2017 Adsorption-mediated mass streaming in a standing acoustic wave. Phys. Rev. Lett. 118 (24), 244301.10.1103/PhysRevLett.118.244301Google Scholar
Yazaki, T., Iwata, A., Maekawa, T. & Tominaga, A. 1998 Traveling wave thermoacoustic engine in a looped tube. Phys. Rev. Lett. 81 (15), 3128–3131.10.1103/PhysRevLett.81.3128Google Scholar