Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T09:40:39.992Z Has data issue: false hasContentIssue false
  • English
  • Français

Acoustic impedance of a cylindrical orifice

Published online by Cambridge University Press:  01 April 2020

Rodolfo Brandão  and
Ory Schnitzer Open the ORCID record for Ory Schnitzer [Opens in a new window]
Rodolfo Brandão
Affiliation:
Department of Mathematics, Imperial College London, LondonSW7 2AZ, UK
Ory Schnitzer*
Affiliation:
Department of Mathematics, Imperial College London, LondonSW7 2AZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

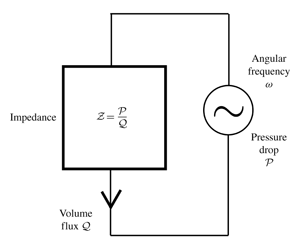
We use matched asymptotics to derive analytical formulae for the acoustic impedance of a subwavelength orifice consisting of a cylindrical perforation in a rigid plate. In the inviscid case, an end correction to the length of the orifice due to Rayleigh is shown to constitute an exponentially accurate approximation in the limit where the aspect ratio of the orifice is large; in the opposite limit, we derive an algebraically accurate correction, depending upon the logarithm of the aspect ratio, to the impedance of a circular aperture in a zero-thickness screen. Viscous effects are considered in the limit of thin Stokes boundary layers, where a boundary-layer analysis in conjunction with a reciprocity argument provides the perturbation to the impedance as a quadrature of the basic inviscid flow. We show that for large aspect ratios the latter perturbation can be captured with exponential accuracy by introducing a second end correction whose value is calculated to be in between two guesses commonly used in the literature; we also derive an algebraically accurate approximation in the small-aspect-ratio limit. The viscous theory reveals that the resistance exhibits a minimum as a function of aspect ratio, with the orifice radius held fixed. It is evident that the resistance grows in the long-aspect-ratio limit; in the opposite limit, resistance is amplified owing to the large velocities close to the sharp edge of the orifice. The latter amplification arrests only when the plate is as thin as the Stokes boundary layer. The analytical approximations derived in this paper could be used to improve circuit modelling of resonating acoustic devices.

Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 892 , 10 June 2020 , A7
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alblas, J. B. 1957 On the diffraction of sound waves in a viscous medium. Arch. Appl. Sci. Res. 6 (4), 237–262.CrossRefGoogle Scholar
Batchelor, G. K. 1967 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Crandall, I. B. 1926 Theory of Vibrating Systems and Sound. D. Van Nostrand Company.Google Scholar
Crighton, D. G., Dowling, A. P., Ffowcs Williams, J. E., Heckl, M. & Leppington, F. G. 1992 Modern Methods in Analytical Acoustics. Springer.CrossRefGoogle Scholar
Crighton, D. G. & Leppington, F. G. 1973 Singular perturbation methods in acoustics: diffraction by a plate of finite thickness. Proc. R. Soc. Lond. 335 (1602), 313–339.Google Scholar
Dagan, Z., Weinbaum, S. & Pfeffer, R. 1982 An infinite-series solution for the creeping motion through an orifice of finite length. J. Fluid Mech. 115, 505–523.CrossRefGoogle Scholar
Daniell, P. J. 1915a The coefficient of end-correction. Part I. Phil. Mag. 30 (175), 137–146.CrossRefGoogle Scholar
Daniell, P. J. 1915b The coefficient of end-correction. Part II. Phil. Mag. 30 (176), 248–256.CrossRefGoogle Scholar
Fang, N., Xi, D., Xu, J., Ambati, M., Srituravanich, W., Sun, C. & Zhang, X. 2006 Ultrasonic metamaterials with negative modulus. Nat. Mater. 5 (6), 452–456.CrossRefGoogle ScholarPubMed
Hinch, E. J. 1991 Perturbation Methods. Cambridge University Press.CrossRefGoogle Scholar
Howe, M. S. 1998 Acoustics of Fluid–Structure Interactions. Cambridge University Press.CrossRefGoogle Scholar
Ingard, U. 1953 On the theory and design of acoustic resonators. J. Acoust. Soc. Am. 25 (6), 1037–1061.CrossRefGoogle Scholar
Jiménez, N., Huang, W., Romero-García, V., Pagneux, V. & Groby, J. P. 2016 Ultra-thin metamaterial for perfect and quasi-omnidirectional sound absorption. Appl. Phys. Lett. 109 (12), 121902.CrossRefGoogle Scholar
King, L. V. 1936 On the electrical and acoustic conductivities of cylindrical tubes bounded by infinite flanges. Phil. Mag. 21 (138), 128–144.CrossRefGoogle Scholar
Kinsler, L. E., Frey, A. R., Coppens, A. B. & Sanders, J. V. 1999 Fundamentals of Acoustics. Wiley.Google Scholar
Komkin, A. I., Mironov, M. A. & Bykov, A. I. 2017 Sound absorption by a Helmholtz resonator. Acoust. Phys. 63 (4), 385–392.CrossRefGoogle Scholar
Laurens, S., Tordeux, S., Bendali, A., Fares, M. & Kotiuga, P. R. 2013 Lower and upper bounds for the Rayleigh conductivity of a perforated plate. ESAIM Math. Model. Numer. Anal. 47 (6), 1691–1712.CrossRefGoogle Scholar
Li, Y. & Assouar, B. M. 2016 Acoustic metasurface-based perfect absorber with deep subwavelength thickness. Appl. Phys. Lett. 108 (6), 063502.Google Scholar
Maa, D. Y. 1998 Potential of microperforated panel absorber. J. Acoust. Soc. Am. 104 (5), 2861–2866.CrossRefGoogle Scholar
Matlab pdetoolbox2019 version 9.10.0 (R2019a).Google Scholar
Melling, T. H. 1973 The acoustic impendance of perforates at medium and high sound pressure levels. J. Sound Vib. 29 (1), 1–65.Google Scholar
Mittra, R. 1971 Analytical Techniques in the Theory of Guided Waves. The Macmillan Company.Google Scholar
Morse, P. M. & Ingard, U. 1986 Theoretical Acoustics. Princeton University Press.Google Scholar
Nomura, Y., Yamamura, I. & Inawashiro, S. 1960 On the acoustic radiation from a flanged circular pipe. J. Phys. Soc. Japan 15 (3), 510–517.CrossRefGoogle Scholar
Norris, A. N. & Sheng, I. C. 1989 Acoustic radiation from a circular pipe with an infinite flange. J. Sound Vib. 135 (1), 85–93.Google Scholar
Peat, K. S. 2010 Acoustic impedance at the interface between a plain and a perforated pipe. J. Sound Vib. 329 (14), 2884–2894.Google Scholar
Rayleigh, Lord 1871 On the theory of resonance. Phil. Trans. R. Soc. Lond. A 161, 77–118.Google Scholar
Rayleigh, Lord 1896 The Theory of Sound. Macmillan.Google Scholar
Sampson, R. A. 1891 On Stokes’s current function. Phil. Trans. R. Soc. Lond. A (182), 449–518.Google Scholar
Sherwood, J. D., Mao, M. & Ghosal, S. 2014 Electroosmosis in a finite cylindrical pore: simple models of end effects. Langmuir 30 (31), 9261–9272.CrossRefGoogle Scholar
Sivian, L. J. 1935 Acoustic impedance of small orifices. J. Acoust. Soc. Am. 7 (2), 94–101.CrossRefGoogle Scholar
Stinson, M. R. & Shaw, E. A. G. 1985 Acoustic impedance of small, circular orifices in thin plates. J. Acoust. Soc. Am. 77 (6), 2039–2042.CrossRefGoogle Scholar
Thurston, G. B. & Martin, C. E. Jr 1953 Periodic fluid flow through circular orifices. J. Acoust. Soc. Am. 25 (1), 26–31.CrossRefGoogle Scholar
Tuck, E. O. 1975 Matching problems involving flow through small holes. Adv. Appl. Mech. 15, 89–158.CrossRefGoogle Scholar
Van Bladel, J. G. 2007 Electromagnetic Fields. Wiley.CrossRefGoogle Scholar
Van Dyke, M. D. 1975 Perturbation Methods in Fluid Dynamics. Parabolic.Google Scholar
Wendoloski, J. C., Fricke, F. R. & McPhedran, R. C. 1993 Boundary conditions of a flanged cylindrical pipe. J. Sound Vib. 162 (1), 89–96.Google Scholar
Zhang, S., Yin, L. & Fang, N. 2009 Focusing ultrasound with an acoustic metamaterial network. Phys. Rev. Lett. 102 (19), 194301.CrossRefGoogle ScholarPubMed
Zwikker, C. & Kosten, C. W. 1949 Sound Absorbing Materials. Elsevier.Google Scholar