Published online by Cambridge University Press: 08 September 2020
The flow structures and the acoustic feedback loops of underexpanded round jets are investigated by numerical simulations. The jets have a Mach number of 1 at the nozzle exit and a diameter-based Reynolds number of  $2.5 \times {10^3}$. Three nozzle pressure ratios (NPRs) of 2.2, 2.4 and 2.6 are considered. The wavelengths of the screech tones are in good agreement with the experimental measurements on high-Reynolds-number jets in the literature. The screech tones are respectively at the A1 and B modes for the jets at NPRs of 2.2 and 2.6. Two screech tones at the A2 and B modes are identified in the jet at the NPR of 2.4 and the wavelet analyses conducted on the pressure fluctuations confirm that these two modes are contemporaneous. The amplitude and phase fields of fluctuating pressure at the screech frequencies are presented in the nozzle exit plane and azimuthal planes. The effective source locations of the screech tones are determined based on the distributions of the phase. The number of periods contained in the screech feedback loop is equal to the number of cells in the standing wave between the nozzle exit and the effective source. The screech frequencies estimated by the classical feedback model agree well with the numerical results at different modes. A modified model, in which the classical feedback model and the upstream-propagating acoustic wave mode of the jet are combined, shows that the screech feedback loops at the A1 and A2 modes are associated with the same acoustic wave mode. The modified model fails to estimate the screech frequencies at the B mode. Different feedback mechanisms lead to the coexistence of the A2 and B modes. The coherent structures corresponding to different screech modes are extracted by dynamic mode decomposition.
$2.5 \times {10^3}$. Three nozzle pressure ratios (NPRs) of 2.2, 2.4 and 2.6 are considered. The wavelengths of the screech tones are in good agreement with the experimental measurements on high-Reynolds-number jets in the literature. The screech tones are respectively at the A1 and B modes for the jets at NPRs of 2.2 and 2.6. Two screech tones at the A2 and B modes are identified in the jet at the NPR of 2.4 and the wavelet analyses conducted on the pressure fluctuations confirm that these two modes are contemporaneous. The amplitude and phase fields of fluctuating pressure at the screech frequencies are presented in the nozzle exit plane and azimuthal planes. The effective source locations of the screech tones are determined based on the distributions of the phase. The number of periods contained in the screech feedback loop is equal to the number of cells in the standing wave between the nozzle exit and the effective source. The screech frequencies estimated by the classical feedback model agree well with the numerical results at different modes. A modified model, in which the classical feedback model and the upstream-propagating acoustic wave mode of the jet are combined, shows that the screech feedback loops at the A1 and A2 modes are associated with the same acoustic wave mode. The modified model fails to estimate the screech frequencies at the B mode. Different feedback mechanisms lead to the coexistence of the A2 and B modes. The coherent structures corresponding to different screech modes are extracted by dynamic mode decomposition.
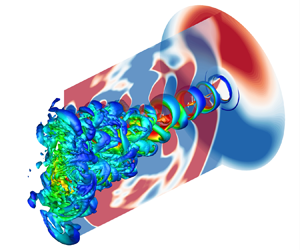
The representation of the isosurfaces of the nondimensional Q-criterion=0.1, colored by the local Mach number, and of the pressure fluctuations in the planes of x=0, θ=π/2 and 3π/2 for the jet at the NPR of 2.2. The nozzle exit is located at x=0.