Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
He, Qing
Tao, Shi
Yang, Xiaoping
Lu, Weijian
and
He, Zongrun
2021.
Discrete unified gas kinetic scheme simulation of microflows with complex geometries in Cartesian grid.
Physics of Fluids,
Vol. 33,
Issue. 4,
Shi, Yangyang
and
Shan, Xiaowen
2021.
A multiple-relaxation-time collision model for nonequilibrium flows.
Physics of Fluids,
Vol. 33,
Issue. 3,
Gan, Yanbiao
Xu, Aiguo
Lai, Huilin
Li, Wei
Sun, Guanglan
and
Succi, Sauro
2022.
Discrete Boltzmann multi-scale modelling of non-equilibrium multiphase flows.
Journal of Fluid Mechanics,
Vol. 951,
Issue. ,
Liu, Xiaochuan
Wu, Si
Zhu, Keyong
Cai, Yuepei
and
Huang, Yong
2022.
Mesoscopic lattice Boltzmann model for radiative heat transfer in graded-index media.
Physical Review Research,
Vol. 4,
Issue. 1,
Zhang, Dejia
Xu, Aiguo
Zhang, Yudong
Gan, Yanbiao
and
Li, Yingjun
2022.
Discrete Boltzmann modeling of high-speed compressible flows with various depths of non-equilibrium.
Physics of Fluids,
Vol. 34,
Issue. 8,
Plotnikov, M. Yu.
and
Shkarupa, E. V.
2023.
Error Estimation and Optimization of the Direct Simulation Monte Carlo Method Taking into Account Spatial Regularization.
Журнал вычислительной математики и математической физики,
Vol. 63,
Issue. 8,
p.
1367.
Chen, Xuan
Yang, Kun
and
Shan, Xiaowen
2023.
Characteristic boundary condition for multispeed lattice Boltzmann model in acoustic problems.
Journal of Computational Physics,
Vol. 490,
Issue. ,
p.
112302.
Plotnikov, M. Yu.
and
Shkarupa, E. V.
2023.
Error Estimation and Optimization of the Direct Simulation Monte Carlo Method Taking into Account Spatial Regularization.
Computational Mathematics and Mathematical Physics,
Vol. 63,
Issue. 8,
p.
1499.
Shi, Yong
2023.
Comparison of different Gaussian quadrature rules for lattice Boltzmann simulations of noncontinuum Couette flows: From the slip to free molecular flow regimes.
Physics of Fluids,
Vol. 35,
Issue. 7,
Jonnalagadda, Anirudh
Sharma, Atul
and
Agrawal, Amit
2023.
On application of the regularized lattice Boltzmann method for isothermal flows with non-vanishing Knudsen numbers.
Numerical Heat Transfer, Part B: Fundamentals,
Vol. 84,
Issue. 6,
p.
756.
Ilyin, Oleg
2024.
Lattice Boltzmann Shakhov kinetic models for variable Prandtl number on Cartesian lattices.
Physical Review E,
Vol. 110,
Issue. 6,
Li, Xiang
Ma, Huaqing
Mei, Zengsheng
Zhou, Du
and
Zhao, Yongzhi
2024.
An approach to determine the solid volume fraction near solid boundaries for partially saturated method within the lattice Boltzmann method.
Computers & Fluids,
Vol. 271,
Issue. ,
p.
106166.
Chen, Zhiping
Zhang, Jia
Zhang, Daren
Chang, Xiaolin
and
Zhou, Wei
2024.
Enhanced permeability prediction in porous media using particle swarm optimization with multi-source integration.
Artificial Intelligence in Geosciences,
Vol. 5,
Issue. ,
p.
100090.
Ilyin, O. V.
2024.
On Accuracy of the Lattice Boltzmann Equations of Low and High Orders as Applied to Slow Isothermal Microflows.
Computational Mathematics and Mathematical Physics,
Vol. 64,
Issue. 9,
p.
2131.
Lei, Timan
Luo, Kai H.
Hernández Pérez, Francisco E.
Wang, Geng
Yang, Junyu
Restrepo Cano, Juan
and
Im, Hong G.
2024.
Pore-scale study of CO2 desublimation and sublimation in a packed bed during cryogenic carbon capture.
Journal of Fluid Mechanics,
Vol. 990,
Issue. ,
Qiu, Ruofan
Yang, Xinyuan
Bao, Yue
You, Yancheng
and
Jin, Hua
2024.
Mesoscopic Kinetic Approach of Nonequilibrium Effects for Shock Waves.
Entropy,
Vol. 26,
Issue. 3,
p.
200.
Nakprapatsorn, Thapana
Wongwaitayakornkul, Pakorn
Malakit, Kittipat
Pianpanit, Theerasarn
and
Ruffolo, David
2025.
Accuracy of two-dimensional high-order lattice Boltzmann method with regularization for transition flows.
Physics of Fluids,
Vol. 37,
Issue. 2,
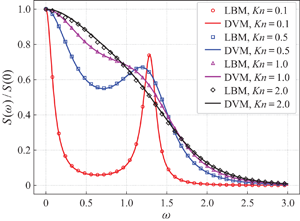
 $Kn=2.0$. Compared with a finite-volume Bhatnagar–Gross–Krook solver using Gauss–Hermite quadrature, the on-lattice LBM has a numerical dissipation several orders of magnitude lower, and achieves the same accuracy with fewer discrete velocities.
$Kn=2.0$. Compared with a finite-volume Bhatnagar–Gross–Krook solver using Gauss–Hermite quadrature, the on-lattice LBM has a numerical dissipation several orders of magnitude lower, and achieves the same accuracy with fewer discrete velocities.