Published online by Cambridge University Press: 21 July 2010
In stratified and rotating fluids, pairs of columnar vertical vortices are subjected to three-dimensional bending instabilities known as the zigzag instability or as the tall-column instability in the quasi-geostrophic limit. This paper presents a general asymptotic theory for these instabilities. The equations governing the interactions between the strain and the slow bending waves of each vortex column in stratified and rotating fluids are derived for long vertical wavelength and when the two vortices are well separated, i.e. when the radii R of the vortex cores are small compared to the vortex separation distance b. These equations have the same form as those obtained for vortex filaments in homogeneous fluids except that the expressions of the mutual-induction and self-induction functions are different. A key difference is that the sign of the self-induction function is reversed compared to homogeneous fluids when the fluid is strongly stratified: |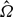 max| < N (where N is the Brunt–Väisälä frequency and
max| < N (where N is the Brunt–Väisälä frequency and 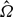 max the maximum angular velocity of the vortex) for any vortex profile and magnitude of the planetary rotation. Physically, this means that slow bending waves of a vortex rotate in the same direction as the flow inside the vortex when the fluid is stratified-rotating in contrast to homogeneous fluids. When the stratification is weaker, i.e. |
max the maximum angular velocity of the vortex) for any vortex profile and magnitude of the planetary rotation. Physically, this means that slow bending waves of a vortex rotate in the same direction as the flow inside the vortex when the fluid is stratified-rotating in contrast to homogeneous fluids. When the stratification is weaker, i.e. |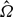 max| > N, the self-induction function is complex because the bending waves are damped by a viscous critical layer at the radial location where the angular velocity of the vortex is equal to the Brunt–Väisälä frequency.
max| > N, the self-induction function is complex because the bending waves are damped by a viscous critical layer at the radial location where the angular velocity of the vortex is equal to the Brunt–Väisälä frequency.
In contrast to previous theories, which apply only to strongly stratified non-rotating fluids, the present theory is valid for any planetary rotation rate and when the strain is smaller than the Brunt–Väisälä frequency: Γ/(2πb2) ≪ N, where Γ is the vortex circulation. Since the strain is small, this condition is met across a wide range of stratification: from weakly to strongly stratified fluids. The theory is further generalized formally to any basic flow made of an arbitrary number of vortices in stratified and rotating fluids. Viscous and diffusive effects are also taken into account at leading order in Reynolds number when there is no critical layer. In Part 2 (Billant et al., J. Fluid Mech., 2010, doi:10.1017/S002211201000282X), the stability of vortex pairs will be investigated using the present theory and the predictions will be shown to be in very good agreement with the results of direct numerical stability analyses. The existence of the zigzag instability and the distinctive stability properties of vortex pairs in stratified and rotating fluids compared to homogeneous fluids will be demonstrated to originate from the sign reversal of the self-induction function.