Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Luo, Kang
Wu, Jian
Yi, Hong-Liang
and
Tan, He-Ping
2016.
Lattice Boltzmann modelling of electro-thermo-convection in a planar layer of dielectric liquid subjected to unipolar injection and thermal gradient.
International Journal of Heat and Mass Transfer,
Vol. 103,
Issue. ,
p.
832.
Luo, Kang
Wu, Jian
Yi, Hong-Liang
and
Tan, He-Ping
2017.
Numerical investigation of heat transfer enhancement in electro-thermo-convection in a square enclosure with an inner circular cylinder.
International Journal of Heat and Mass Transfer,
Vol. 113,
Issue. ,
p.
1070.
Luo, Kang
Li, Tianfu
Wu, Jian
Yi, Hong-Liang
and
Tan, He-Ping
2018.
Electro-thermo-convective flow of a dielectric liquid due to nonautonomous injection of charge by an elliptical electrode.
International Journal of Heat and Mass Transfer,
Vol. 127,
Issue. ,
p.
373.
Luo, Kang
Wu, Jian
Yi, Hong-Liang
Liu, Lin-Hua
and
Tan, He-Ping
2018.
Hexagonal convection patterns and their evolutionary scenarios in electroconvection induced by a strong unipolar injection.
Physical Review Fluids,
Vol. 3,
Issue. 5,
Luo, Kang
Wu, Jian
Yi, Hong-Liang
and
Tan, He-Ping
2018.
Three-dimensional finite amplitude electroconvection in dielectric liquids.
Physics of Fluids,
Vol. 30,
Issue. 2,
Lu, Zhiming
Liu, Guoqing
and
Wang, Bofu
2019.
Flow structure and heat transfer of electro-thermo-convection in a dielectric liquid layer.
Physics of Fluids,
Vol. 31,
Issue. 6,
Luo, Kang
Pérez, Alberto T.
Wu, Jian
Yi, Hong-Liang
and
Tan, He-Ping
2019.
Efficient lattice Boltzmann method for electrohydrodynamic solid-liquid phase change.
Physical Review E,
Vol. 100,
Issue. 1,
Guan, Yifei
and
Novosselov, Igor
2019.
Numerical analysis of electroconvection in cross-flow with unipolar charge injection.
Physical Review Fluids,
Vol. 4,
Issue. 10,
Luo, Kang
Wu, Jian
Pérez, Alberto T.
Yi, Hong-Liang
and
Tan, He-Ping
2019.
Stability analysis of electroconvection with a solid-liquid interface via the lattice Boltzmann method.
Physical Review Fluids,
Vol. 4,
Issue. 8,
Li, Fang
Wang, Bo-Fu
Wan, Zhen-Hua
Wu, Jian
and
Zhang, Mengqi
2019.
Absolute and convective instabilities in electrohydrodynamic flow subjected to a Poiseuille flow: a linear analysis.
Journal of Fluid Mechanics,
Vol. 862,
Issue. ,
p.
816.
Dutta, Satarupa
Ghosh, Abir
Pattader, Partho Sarathi Gooh
and
Bandyopadhyay, Dipankar
2019.
Electric field mediated von Kármán vortices in stratified microflows: transition from linear instabilities to coherent mixing.
Journal of Fluid Mechanics,
Vol. 865,
Issue. ,
p.
169.
Guan, Yifei
and
Novosselov, Igor
2019.
Two relaxation time lattice Boltzmann method coupled to fast Fourier transform Poisson solver: Application to electroconvective flow.
Journal of Computational Physics,
Vol. 397,
Issue. ,
p.
108830.
Guan, Yifei
Riley, James
and
Novosselov, Igor
2020.
Three-dimensional electroconvective vortices in cross flow.
Physical Review E,
Vol. 101,
Issue. 3,
Su, Zheng-Gang
Zhang, Yi-Mo
Luo, Kang
and
Yi, Hong-Liang
2020.
Instability of electroconvection in viscoelastic fluids subjected to unipolar injection.
Physics of Fluids,
Vol. 32,
Issue. 10,
He, Kun
Chai, Zhenhua
Wang, Lei
Ma, Ben
and
Shi, Baochang
2021.
Numerical investigation of electro–thermo-convection with a solid–liquid interface via the lattice Boltzmann method.
Physics of Fluids,
Vol. 33,
Issue. 3,
Wang, Qi
Guan, Yifei
Huang, Junyu
and
Wu, Jian
2021.
Chaotic electro-convection flow states of a dielectric liquid between two parallel electrodes.
European Journal of Mechanics - B/Fluids,
Vol. 89,
Issue. ,
p.
332.
He, Xuerao
and
Zhang, Mengqi
2021.
On the flow instability under thermal and electric fields: A linear analysis.
European Journal of Mechanics - B/Fluids,
Vol. 88,
Issue. ,
p.
34.
Li, Gaojin
Townsend, Alex
Archer, Lynden A.
and
Koch, Donald L.
2021.
Suppression of electroconvective and morphological instabilities by an imposed cross flow of the electrolyte.
Physical Review Fluids,
Vol. 6,
Issue. 3,
Wan, Dongdong
Sun, Guangrui
and
Zhang, Mengqi
2021.
Subcritical and supercritical bifurcations in axisymmetric viscoelastic pipe flows.
Journal of Fluid Mechanics,
Vol. 929,
Issue. ,
Selvakumar, R. Deepak
Qiang, Liu
Kang, Luo
Traoré, Phillipe
and
Wu, Jian
2021.
Numerical modeling of solid-liquid phase change under the influence an external electric field.
International Journal of Multiphase Flow,
Vol. 136,
Issue. ,
p.
103550.
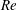 $Re$ cross-flow is also considered for investigating the combined effect of inertia and the electric field. It is found that the base cross-flow is modified by the electric effect and that, even when the inertia is dominating, the electric field can still strengthen effectively the subcritical characteristics of canonical channel flow. In this process, however, the electric field does not contribute directly to the subcriticality of the resultant flow and the intensified subcritical feature of such flow is thus entirely due to the modified hydrodynamic field as a result of the imposed electric field. This finding might be important for flow control strategies involving an electric field. Theoretically, the above results are obtained from a multiple-scale expansion method, which gives rise to the Ginzburg–Landau equation governing the amplitude of the first-order perturbation. The conclusions are deduced by probing the changes of value of the coefficients in this equation. In particular, the sign of the first Landau coefficient indicates the type of bifurcation, being subcritical or supercritical. Moreover, as a quintic-order Ginzburg–Landau equation is derived, the effects of higher-order nonlinear terms in EHD flow are also discussed.
$Re$ cross-flow is also considered for investigating the combined effect of inertia and the electric field. It is found that the base cross-flow is modified by the electric effect and that, even when the inertia is dominating, the electric field can still strengthen effectively the subcritical characteristics of canonical channel flow. In this process, however, the electric field does not contribute directly to the subcriticality of the resultant flow and the intensified subcritical feature of such flow is thus entirely due to the modified hydrodynamic field as a result of the imposed electric field. This finding might be important for flow control strategies involving an electric field. Theoretically, the above results are obtained from a multiple-scale expansion method, which gives rise to the Ginzburg–Landau equation governing the amplitude of the first-order perturbation. The conclusions are deduced by probing the changes of value of the coefficients in this equation. In particular, the sign of the first Landau coefficient indicates the type of bifurcation, being subcritical or supercritical. Moreover, as a quintic-order Ginzburg–Landau equation is derived, the effects of higher-order nonlinear terms in EHD flow are also discussed.